Oeuvres complètes. Tome I. Correspondance 1638-1656

N^o 21.
Christiaan Huygens à [M. Mersenne.]
[1646].

La minute se trouve à Leiden, coll. Huygens¹⁾.

1) Voir la note 1 du N^o. 20. Les Propositions 1-4 ont pu être reconstruites à l'aide de quelques autres papiers de Chr. Huygens, qui se trouvaient parmi ses adversaria; on y a laissé la nomenclature qu'ils avaient, c'est-à-dire Axiomata 1-5, Lemmata 1, 2, Propositiones 1-3, dont la troisième coïncide avec la cinquième de notre lettre. On trouvera cette reconstruction au N^o. 22.
Les Axiomata 1-4 y remplacent les suppositions 1-4 du N^o. 20.

Propositio 5.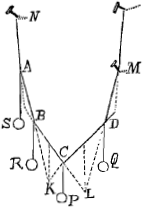

Si il y a tant de gravitez qu'on veut comme S, R, P, Q pendues à une corde ABCD. je dis que MD et BC continuées s'entre-couppent en L au diametre pendule des gravitez P et Q. AB et DC en K au diametre pendule des gravitez R et P et ainsi du reste. Car si on arreste^a) quelque deux poincts A et D (en laissant deux autres entre deux comme B et C), en la situation ou ils sont, cela ne changera poinct celle des poincts B et C^b); mais les poincts A et D estants arrestez, l'intersection des continuées AB et DC^c) doit estre au diametre pendule des gravitez R et P. C'est donc signe qu'aussi auparavant elle ij a esté: Et ainsi le prouvera ton des autres.

a) muta [Chr. Huygens.]

b) demande 3. [Chr. Huygens.]

c) Prop 2. [Chr. Huygens.]

[p. 36]

Propositio 6.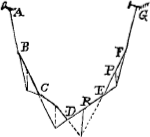

Eadem methodo probatur si AB, BC, CD etc sint virgulae ponderantes^d) aequalis ponderis, quasque duas productas ut CD, FE, sese intersecare in pendula gravitatis diametro ejus quae intermedia relicta est ut DE. Ergo si omnes aequalis sunt ponderis, DR debet aequalis esse RE, EP aequalis PF etc.^e)

d) muta [Chr. Huygens.]

e) Prop. 4 [Chr. Huygens.]

Propositio 7.

Si sint quotcunque pondera vel virgulae aequalis ponderis eo situ ut bina quaeque internodia ut BC, ED producta sese invicem intersecent in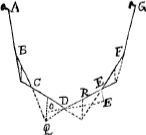



pendula gravitatis diametro intermedia CD, dico hunc situm esse, quo pendere possunt, et debent.

Si enim punctum D firmetur apparet quidem virgulas AB, BC, CD dato situ mansuras: porro autem si firmetur punctum E omisso D, dico punctum D tamen è loco non recessurum, ideoque virgulas AB, BC, CD, DE dato situ mansuras; si enim firmato puncto E punctum D mutare locum dicatur, (quia ergo per 4 tam suppositionem possibile est punctum E eo loci teneri ut punctum D locum non mutet) sit hoc in E. Dicatur itaque oportet hoc situ punctum D locum non mutaturum; Ergo neque si praeterea firmetur punctum B; Sed quoniam ED producta conveniebat in pendula gravitatis diametro cum producta BC, ED producta non illic concurret; Ergo neque firmatis punctis B et E virgulae hunc situm habere possunt,^f) ergo neque punctum D. Quia itaque videmus punctum E extra datum locum teneri non posse, ut punctum D suum non mutet, necessario sequitur ex dicta 4^ta suppositione datum locum eum esse. Quod erat demonstrandum. Eadem ratione de caeteris punctis F et G demonstrabitur.

f) Per Prop. 2 [Chr. Huygens.]

Propositio 8.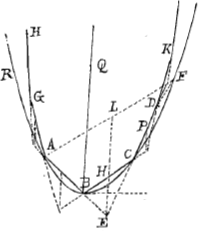

Sit suspensa catena HGABCDK constans virgulis aequalis longitudinis, ponderis et figurae; dico puncta juncturarum GABCDK non posse coincidere in eandem lineam parabolicam.

Ex propositione 6 apparet quomodo hae virgulae pendere debeant nempe ut H sit in media BC, P in media CD etc. Sit itaque nunc descripta parabola RABCF per tria puncta ABC transiens, dico non transire hanc per punctum D et reliqua: producatur enim ECD donec sit FC ad CE ut AB ad BE, ergo ducaturque AF, haec ergo et parallela erit BC et similiter à linea EL in L bifariam secabitur, ideoque erit punctum F in eadem parabolâ cum punctis ABC, nam EL est diameter parabolae B, et non punctum D. alias enim linea ECDF deberet parabolicam in tribus punctis secare quod est absur-

[p. 37]

dum, vel punctum D coincidere cum puncto F quod impossibile est, nam FC major



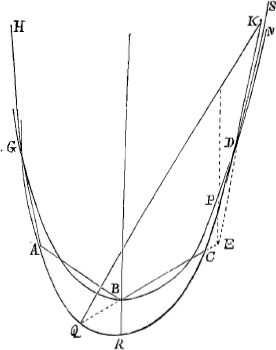est AB sive DC, quia CE major est BE. Quia itaque parabola descripta per puncta ABC, non transit per punctum D; etiam ea quae per puncta GBD describitur, non transit per puncta A et C sed ea excludit. Demonstrabo autem neque eam per puncta H et K transire; descripta enim sit alia parabola GARCDS, quae transeat per puncta G, A, C, D, quae ideo secabit priorem parabolam in G et D; si itaque parabola GARCDS demonstrata fuerit non transire per puncta H et K, multo minus per ea transibit altera GBDN. At hoc sic demonstratur; Prolongetur EB usque dum occurrat parabolae GARCDS in Q, quia itaque puncta D, C et Q sunt in parabola GARCDS et linea CD in P à diametro parabolae EP bifariam dividitur,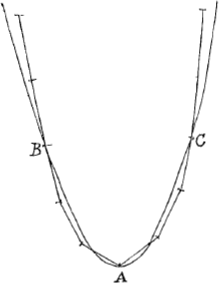



oporteret si punctum K in eadem esse dicatur, ut EC esset ad CQ sicut ED ad DK, hoc vero fieri nequit, cum etiamsi CQ non esset longior DK, tamen DE longior sit CE: cum itaque punctum K non possit esse in parabola GARCDS, multo minus erit in parabola GBD, quod erat demonstrandum.

Hac ratione iterum demonstrari potest parabolam quae per puncta HBK descripta est non transire per extremitates sequentium virgularum: et sic in infinitum.

Propositio 9.

Unde itaque manifestum fit, si sit suspensa catena composita ex virgulis ejusdem longitudinis et gravitatis, parabolam quae describitur per extremum ejus A, et duo alia ejus puncta B et C, per nulla alia ejus puncta transire, sed excludere ea omnia quae infra dicta puncta B et C sunt, includere vero ea quae ijs superiora sunt. Nulla ergo catena pendet secundum lineam parabolicam.

Propositio 10.

Sed ne quis putet quod si ex virgulis valde minutis esset composita, nulla notabilis differentia futura foret inter lineam secundum quam penderet et lineam parabolicam, consideretur catena ABCDEFGHI, composita ex infinitis numero vir-

[p. 38]

gulis; Et dico nullam notabilem differentiam esse inter lineam secundum quam pendet, et eam secundum quam penderet si esset composita ex virgulis aequalibus AB, BC, CD etc. Ponatur enim inflexibilis fieri catena composita ex virgulis



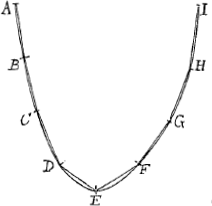infinitis, praeterquam in punctis A, B, C, D etc.^g) habebimusque catenam quae constat ex virgulis incurvatis aliquantum, quae quum sibi invicem tum pondere tum figura quam proxime aequales sint, eodem penè modo pendere debebunt ac virgulae rectae AB, BC etc. ergo et antea catena sic pendebat. quod erat demonstrandum.

Lemma.²⁾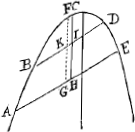

Si duas parallelas lineas BD, AE parabolas utrinque occurrentes diameter parabolae CH in eandem proportionem dividat, utramque bifariam secabit. Si enim dicantur non bifariam sectae in I et H secentur ab alia diametro FG bifariam in K et G. quoniam igitur BK est ad AG ut BD ad AE et etiam BI est ad AH ut BD ad AE, erit BI ad AH ut BK ad AG. et ablatis hinc AG inde BK, remanet KI ad GH ut BK ad AG, quod est absurdum cum KI, GH sint aequales: BK, AG inaequales.

g) Hoc enim non mutabit ejus figuram. [Chr. Huygens.]

2) Dans la minute ce Lemma est rayé.

Propositio 11.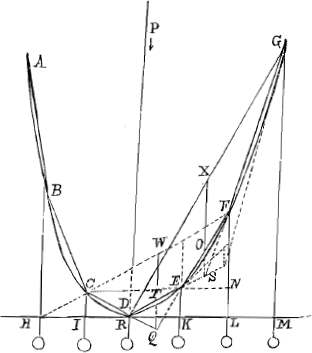

Sit ABCDEFG parabola cujus diameter PD perpendicularis ad horizontem HM sit linea eam in vertice D contingens, quae utrimque ex D in quotlibet aequales partes sit divisa in KLM etc. Hincque perpendiculares erigantur CI, KE, LF, MG, et per puncta ubi parabolae occurrunt B, C, E, F, G, filum tendatur, et filo huic in ijsdem punctis aequalia pondera HIRKLM appendantur; dico, si haec catena in punctis A et G ligetur, ex ijsque libere pendeat, omnia puncta B, C, D, E, F eundem locum retentura quem ante habebant. Producantur namque CD, FE usque ad intersectionem in Q; DE, GF usque ad intersectionem in S. Cum igitur per prae-

[p. 39]

missum lemma Q sit in pendula gravitatis diametro ponderum D et E, S in pendula gravitatis diametro ponderum E et F, sequitur per propositionem 7. non alio quam hoc situ pendere posse. Primo sciendum est KE esse 1, LF 4, MG 9 et sic deinceps.

Propositio 12.

Sint appensa filo IGCFH, aequalia pondera, et interstitia AB, BC, CD, DE sint aequalia, dico puncta IGCFH in eadem esse parabola. Cum enim pendere dicantur, sequitur ex propositione 5, productas GC, HF invicem intersecare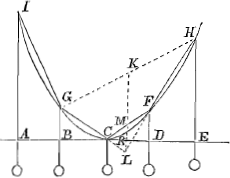



in L, in pendula gravitatis diametroponderum pendentium ex C et F. cum igitur LM secet CF bifariam in M, secabit quoque producta bifariam lineam GH, cum spatia BR, RE sint aequalia; et quia GLH est triangulum et in eo lineae GH, CF ex angulo L in eandem proportionem sectae, necessario quoque sunt parallelae, atque adeo puncta G, C, F, H, in eadem parabola cujus diameter KL. Sic quoque demonstratur punctum I in eadem parabola esse cum punctis GCF ergo omnia in eadem parabola, quod erat demonstrandum.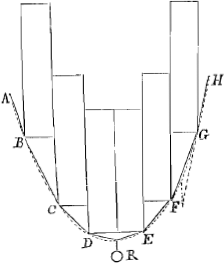

Manifestum. φανερὸν.

Hinc manifestum est si filo ABC etc imponantur trabeculae seu parallelepipeda aequalis ponderis, magnitudinis et figurae, puncta ABC etc in quibus filum premunt, omnia futura esse in eadem parabola, si nempe eo ordine disposita sint ut D et E, C et F, B et G aequali sint altitudine infra vero unica gravitas R appendatur. Cum autem quo minor est latitudo parallelepipedorum eo minoris sit momenti, duplicatio ponderis parallelepipedi infimi; constat inde si infinita sit eorum multitudo, eam ne quidem in considerationem venire.

Hinc porro manifestum fit quaenam pressio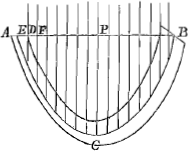



requiratur supra filum seu lineam mathematicam flexibilem, ut parabolae circumferentiam flectatur, ea scilicet quae secundum latitudinem aequabiliter premit; Sic si sit filum ACB quod teneatur in A et B linea autem quae puncta haec jungit divisa sit in quotlibet partes aequales ut AE, ED, DF etc. fiat autem pressio aequalis in filum dictum, per unumquodque spatiorum AE, ED, DF etc. hanc voco pressionem aequabilem secundum latitudinem. Talem vero ven-

[p. 40]

tus efficit, et aqua fluens, adeo ut si velum ABC quod ubique aequalis sit latitudinis suo impetu tendant, illud figuram parabolicam sit relaturum.

Talis item est quam aqua efficeret si tanta altitudine velo ABC superstaret ut altitudo CP in considerationem non veniret, quia videlicet exterior ejus superficies semper plana est.

Denique talis est quâ aqua premit retia piscatorum vel simile quid, quae in eâ vi protrahuntur.

Unde et haec videmus parabolam referre.