Oeuvres complètes. Tome I. Correspondance 1638-1656

N^o 22.
Christiaan Huygens à [M. Mersenne].
[1646].

Pour compléter les Nos. 20 et 21.
Le manuscrit se trouve à Leiden, coll. Huygens.

Axiomata.

1.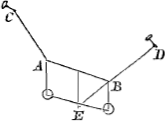

Omnes chordae ex quibus gravitas libere pendet supponuntur parallelae inter se; et eadem ratione pondera non ad centrum sed ad planum descendere conari.

2

Duae vel plures gravitates, ut A et B, alligatae chordae CABD, quae tenetur in punctis C et D, non possunt nisi unico situ quiescere: idque tali ut centrum gravitatis earum, quod hic est E, quantum potest descendat et plano terrae admoveatur.

3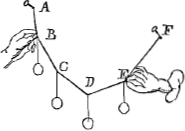

Si ex chorda aliqua ADF pendeant gravitates quotlibet BCDE in situ a natura requesito, et unum duo quaelibet puncta ut B, E, in eo quo sunt situ retineantur, caeterorum ut C, D, situs ideo non mutabitur.

[p. 41]

4.

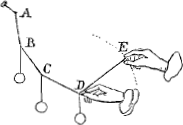Si quotlibet gravitates B, C, D, sint annexae chordae A, B, C, D, E, et retento puncto D, gravitates B et C pendeant in situ naturali; potest extremitas E ita disponi, ut punctum D derelictum eodem tamen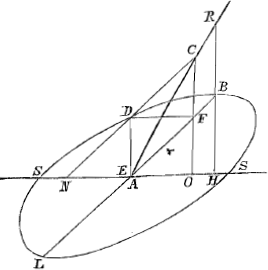



loco maneat, et per consequens etiam reliquae gravitates B et C.

5.

Pars finita circumferentiae circuli infinitae magnitudinis aequipollet rectae lineae. exemplum addendum.

Lemma 1.

Sit angulus SAR, intra quem moveatur regula NDC, sitque ejus medium D. dico punctum D hoc motu partem ellipseos SDB describere. Sit HR aequalis NC et perpendicularis in SHS ex medio ejus B per A ducatur BAL, sumtisque SA utrinque aequali ND, describatur circa diametros conjugatas SAS, LAB ellipsis. demonstrandum est punctum D esse in hac ellipsi. ducatur ex D ordinatim applicata DF ad diametrum LB. ducaturque praeterea ex C termino regulae CO perpendicularis in NHS quae necessario per F transibit, quum linea CO in duas aequales secetur tam a DF, quam ab AB, ab hac quia RB et BH aequales sunt, ab illa quia ND, DC itidem sunt aequales et DF parallela NO.

Demonstratio¹⁾ quadratum BA est ad rectangulum BFL sive differentiam quadratorum BA, AF, ut quadratum BH ad differentiam quadratorum BH, FO, vel ut quadratum EF ad quadratum EO; (quia FE aequalis est BH et per hoc quadratum EO aequale differentiae quadratorum BH, FO). atqui cum aequales sint EO et DF, est quadratum EF ad quadratum EO ut idem quadratum EF ad quadratum DF, ergo et quadratum AB ad rectangulum BFL ut quadratum EF seu AS ad quadratum DF et permutatim quadratum AB ad quadratum AS ut rectangulum BFL ad quadratum DF, et consequenter per pr. 21.1 l. Con. Ap.²⁾ punctum D in ellipsi.

1) Pour comprendre cette démonstration, on doit distinguer le point A, le centre de l'ellipse, de E, à demi-distance entre N et O, de sorte que EF est parallèle à NC.

2) C'est-à-dire: Proposition 21 du Livre I des Coniques d' Apollonius.

Lemma 2.

Sit angulus SAQ, intra quem motu regulae TDQ punctum D quod in medio regulae est descripserit ellipsin SNDRS, in Ellipsi hac punctum sumatur quodcunque D, transeatque per illud regula TDQ. et ubi lateribus anguli SAQ utrinque occurrit ducantur inde in eadem latera perpendiculares QF, et TF, et ex puncto intersectionis earum F ducatur recta FD, ad punctum D sumptum in ellipsi; Dico hanc

[p. 42]

FD ellipsi occurrere ad angulos rectos, sive erectam super DF perpendicularem DL, contingere ellipsin in puncto D.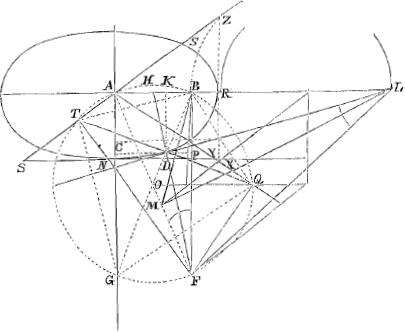

Preparatio. Ducatur AF eâque diametro describatur circulus ABQFG, qui, quia anguli ATF, AQF recti sunt transibit per puncta T et Q. Porro dividatur angulus SAQ bifariam recta AG et in eam perpendicularis statuatur AR quae axis erit ellipseos, et ubi AG circumferentiae circuli occurrit, inde ducatur per D recta GDB, quae (quum anguli TAG, GAQ, et per hoc partes circumferentiae quibus insistunt TG, GQ sint aequales ut et lineae TD, DQ) secabit lineam TDQ ad angulos rectos, ideoque transibit etiam per centrum circuli O, occurretque praeterea circumferentiae circuli in B ubi eadem à recta AR secatur, quia angulus GAB rectus est. Ducatur etiam ex B, BF perpendicularis in AR (quae necessario incidet in punctum F, quia angulus ABF rectus est et AF diameter) et ei parallela DK, cadatque super AG perpendicularis DC. (AB ad AM ∞ AF ad AL). Denique ex N ubi AG ellipsin intersecat ducatur tangens SY, et similiter ex vertice ellipseos R ducatur tangens ZX. et postremo jungantur TB, BQ, TG, GQ.

Demonstratio. AK est ad KB ut GC ad KD: KB ad KH ut FP sive GC ad KD. ergo AK ad KB ut KB ad KH. ergo AK ad KH. ut □ AK ad □ KB, vel ut □ GD ad □ DB, vel ut □ AR ad □ AN, ergo LD tangit ellipsin, per lemma praecedens³⁾.

AR est aequalis GD quia triangulum XAZ simile et aequale Δ^o TGQ. Item AN ∞ DB quia Δ SAY simile et aequale Δ^o TBQ. nam SY ∞ TQ et ∠ SAY ∞ TBQ.

3) Il veut dire: Sequens.

Lemma.

Sit ellipsis ACB, diameter AB, centrum F, et in circumferentia ejus punctum C. et ordinatim applicata CD, et quam proportionem habet latus transversum ellipseos ad latus rectum eam habeat FD ad DE. et in CE sit perpendicularis CG, quae conveniat cum producta AB in G, dico hanc in C contingere ellipsin.

Praeparatio. diametro AB centro F describatur semicirculus AKB, et produ-

[p. 43]

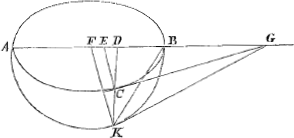catur DC usque ad ejus circumferentiam in K, ducaturque FK et in eam perpendicularis statuatur KG. jungaturque KB. Demonstratio. Rectangulum ADB sive quadratum DK est ad quadratum DC ut latus transversum figurae ad latus rectum, per 21.1. Con. Apoll. sed et FD est ad ED in eâdem ratione ex constructione, ergo quadratum KD ad quadratum CD ut FD ad ED et permutando FD ad quadratum DK ut ED ad quadratum DC. ergo DG quae fit ex applicatione FD ad quadratum KD aequatur eidem DG quae fit ex applicatione lineae ED ad quadratum DC. unde apparet tangentes circuli et ellipseos CG, et KG coincidere in prolongata diametro AB in eodem puncto G. Jam porro rectangulum GDF aequatur quadrato DK. additoque utrinque quadrato DF aequatur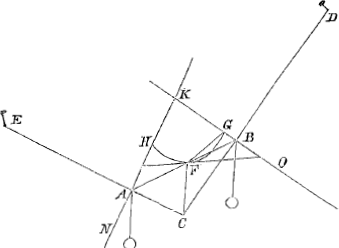



rectangulum GFD quadrato FK sive FB, unde sequitur per 37. 1. Con. Apoll. lineam GC ellipsin in C contingere. quod erat demonstrandum.

Propositio 1.

Quia prolongatio partium funis EA, DB non mutat situm ponderum, imaginemur eas quantumlibet magnae imo infinitae esse longitudinis ita ut partes circumferentiae circulorum descriptorum radijs EA et DB centris E, [D]³⁾ represententur nobis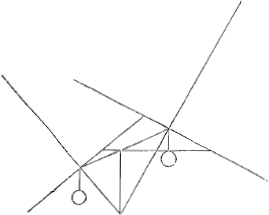



per rectas KBO, KAN quae ideo ad EA et DB sint ad angulos rectos. et cum pars funis AB semper extensa maneat, oberretque semper extremitatibus suis lineas KBO, KAN, apparet manifesto per lemm...⁴⁾ punctum F quod in medio ejus est si moveatur non nisi ellipsin describere posse; quumque CB ad KO faciat angulos rectos ut et CA ad KN et ab intersectione earum ducta sit CF ad ellipsin, mediamque AB, patet ex lemm....⁵⁾ FO quae perpendi-

3) Il veut dire: Sequens.

4) Le papier était déchiré à cet endroit.

5) Chr. Huygens indique ce Lemma par...Ce sont les Lemmata 1 et 2, de page 41.

[p. 44]

cularis est ad CF, contingere ellipsin in F. ideoque punctum F in medio funis AB etiamsi moveatur non posse amplius descendere, ergo neque antea quum funes EA, DB breviores essent amplius descendere potuit.

Manifestum.

Hinc sequitur duo dicta pondera non posse pendere alio situ quam ut productae EA, DB invicem intersecent in pendula gravitatis diametro; nam quum demonstratum sit situm hunc eorum naturalem esse cum sic pendent, et tantum uno situ possint pendere, sequitur necessario eum hunc esse.

Propositio 2.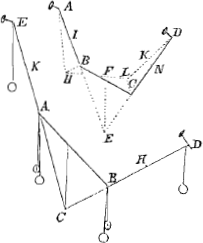

Sint AB, BC, CD virgulae ponderantes similes invicem et aequales, atque ita junctae in B et C ut ibidem libere flecti et circa paxillos A et D circumagi possint. dico eas ita pendere debere ut extremae productae intersecent se invicem in pendula gravitatis diametro ejus quae media est. Sint I, F, K centra gravitatis virgularum. Quia enim per praecedentem dicto situ punctum F quantum potest descendit per propositionem antecedentem adeoque si moveatur ascendit, sequitur si punctum B locum mutet veniatque ad H, punctum F ascensurum, sed cum hinc etiam necessario sequatur punctum B minus descendere cum ad H pervenit quam punctum C ascensurum sit sive I minus descendere quam K ascendat, manifestum est etiam centrum gravitatis quod est inter duas virgulas AB, DC ascensurum; igitur omnium virgularum centrum gravitatis ultro ascenderet quod est absurdum.

Propositio 3.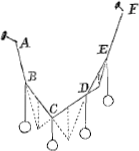

Si quotlibet aequalia pondera ex punctis B, C, D, E funi appensa sint, dico quaelibet duo internodia, uno intermedio relicto, producta concurrere in pendula gravitatis diametro duorum ponderum intermediorum quae pendent ex C et D. Dicatur enim producta internodia BC, ED non concurrere in pendula gravitatis diametro ponderum ex C et D pendentium, et firmentur puncta B et E eo quo sunt loco. Igitur quia secundum 3^m axioma punctorum C et D situs eo non mutatur, sequeretur ne tunc quidem cum puncta B et E retinentur, BC et ED productas sibi invicem occurrere in pendula gravitatis diametro ponderum ex C et D pendentium quod est contra propositionem primam.