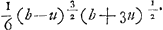Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–No 2838.
| |
[pagina 564]
| |
cette matiere autant qu'elle le merite, je craignois de ne pouvoir m'en ressouvenir, et c'est ce qui m'avoit empesché jusqu'a present de vous faire reponce sur cet article. Cependant des que j'ay receu vôtre derniere, je me suis appliqué avec soin à rechercher ce qu'il m'avoit communiqué et je trouve que c'est à peu près ce qui suit. Jl pretend que la voile AFB attachée par ses extremités A et B, et enflée par le vent en sorte que la ligne AD perpendiculaire à la direction CA du vent touche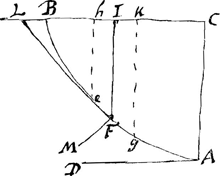 la voile en A, se courbe de la mesme maniere que ferait une chaîne egale par son propre poids en concevant alors que la tangente AD fust horizontale. C'est à dire pour oster tout equivoque que si l'on conçoit que la voile AFB soit divisée en un nombre infini de petits parallelogrammes gF, Fe égaux, inflexibles et sans pesanteur, ils forment la mesme courbure etant etendus par le vent qu'ils feroient par leur propre poids en faisant partie de la chaîne AFB. Voici les suppositions dont il se sert pour demontrer ce theorème. 1o Que les petites parties qui composent le vent peuvent estre considerées comme de petites globules. 2o Que ces petits globules après avoir heurté contre la voile s'ecartent librement et sans trouver d'obstacle; d'ou il suit que chaque globule comme I heurte la voile en F selon la perpendiculaire FM à la tangente FL qui passe par le point de rencontre F avec une force diminuée qui est à sa force totale comme le sinus LI de l'angle d'incidence IFL est au sinus total FL. 3o Que si l'on prend sur la courbe AFB, les parties gF, Fe egales entr'elles, le nombre des petits globules qui heurtent en mesme temps c'est à dire de compagnie contre la partie eF n'est pas egal à celui des globules qui heurtent aussi en mesme temps ou de compagnie contre la partie Fg, mais que ces nombres sont entr'eux comme hI est à Ik; les lignes eh, FI, gk sont paralleles à la direction CA du vent. 4o Que si l'on attache la voile en F supposant que la partie FB soit retranchée; la partie restante FA ne changera point de courbure. Ces suppositions etant ainsi faites il me paroît que tout le reste se tire par des consequences legitimes. C'est donc à vous Monsieur de faire voir que quelqu'une de ces hypotheses est fausse puisque vous pouvez demontrer que la conclusion ou elles conduisent n'est pas vraye. Vous me ferez plaisir de me faire part de ce que vous en pensez. Vôtre remarque sur le livre de la manoeuvre des vaisseaux est tres exacte et ne souffre point de replique, je m'etonne aussi bien que vous que personne ne l'ait encore remarqué. Je n'ai point encore lû ce livre, quoi qu'il soit fort petit et que l'autheur soit beaucoup de mes amis, j'avois toujours remis à le lire lorsque j'aurois achevé certaines speculations qui m'occupoient, ce n'est pas que je | |
[pagina 565]
| |
n'eusse fort bien pû passer cet endroit car il est facile de se tromper lorsque la geometrie se trouve jointe à la phisique, et c'est neanmoins en cela que je fais consister sa plus grande utilité. Je vous suis fort obligé de ce que vous avez bien voulu me faire part de la maniere dont vous décrivez les courbes de Mr. Bernoulli qui est sans comparaison meilleure que la sienne. Je n'ai pas eu de peine à comprendre la raison de la longueur des diametres que vous prescrivez pour les rouleaux car elle saute d'abort aux yeux. J'ai aussi trouvé plusieurs manieres de determiner le point C dont voici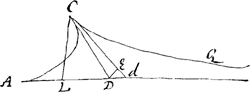 la plus simple et ou il n'est pas besoin de calcul. Je remarque que les tangentes CD de la partie AC et Cd de la partie CQ, qui font entr'elles l'angle DCd infiniment petit ont pour difference la petite droite Ed en menant DE perpendiculaire sur CD, et que si l'on mene CL perpendiculaire sur AD les triangles DdeGa naar voetnoot2), CDL seront semblables. Or par la proprieté de la courbe Ad:dC∷AD:DC∷ ∷Ad-AD ou Dd:Cd-CD ou Ed∷DC:DL; d'ou l'on voit que sous le point C les lignes AD, DC, DL sont en proportion continuë, et par consequent qu'il ne se rencontre que dans les lignes ou AD surpasse DC. Je suis parfaitement d'accord avec vous Monsieur sur ce que vous me mandez touchant la necessité d'une seconde suitte pour les quadratures outre celle de Mr. Gregori ou la mienne qui est équivalenteGa naar voetnoot3), car lorsque je vous ai mandé pouvoir demontrer qu'il en falloit une ma raison étoit qu'en supposant x=0 on trouvoit une quantité constante bien que l'on sçust d'ailleurs que l'efpace fust alors nulle, d'ou je concluois qu'il falloit retrancher cette quantité de la quadrature trouvée, et il est si vrai, que ç'a toujours esté la ma pensée que je n'ai formé ma 3e suitteGa naar voetnoot4) qu'en supposant dans la 2e x=0. Et ainsi tout ce que j'ai prettendu étoit que la suitte de Mr. Gregori ne donne pas au juste l'espace compris par l'abscisse x et l'appliquée y, et qu'il en falloit toujours retrancher une certaine quantité que l'on peut trouver en supposant x=0, ou dans la quadrature trouvée, ou dans une autre suitte que l'on formera dont il faudra prendre aussi la somme ce qui revient au mesme. Au reste toutes ces suittes ne sont point necessaires lorsque c est un nombre entier, car je puis toujours prouver alors les quadratures sans en avoir besoin. Je crois que pour repondre à tout ce que vous souhaitez de | |
[pagina 566]
| |
moi je n'ai qu'a vous envoyer la 3e maniereGa naar voetnoot5) dont je quarre la feuille de Descartes, qui est celle-ci. Soit AF=u, FC=z, AD=b; l'équation x3+y3=axy (dans laquelle x, y et a marquent AB, BCGa naar voetnoot6) et b √2) je change en cette autre 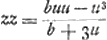 et si l'on change les signes ou u a une dimension impaire, on trouve et si l'on change les signes ou u a une dimension impaire, on trouve 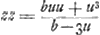 , d'où l'on connoist que la courbe DCA se continuë vers C, K en sorte que, si l'on prend u=⅓ b=AE l'appliquée z qui est en ce cas EL devient infinie, c'est-à-dire asymptote. Or l'element de l'espace DCF, savoir , d'où l'on connoist que la courbe DCA se continuë vers C, K en sorte que, si l'on prend u=⅓ b=AE l'appliquée z qui est en ce cas EL devient infinie, c'est-à-dire asymptote. Or l'element de l'espace DCF, savoir 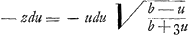 et celui de l'espace KCFEL infiniment etendu du côté de KL= et celui de l'espace KCFEL infiniment etendu du côté de KL=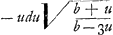 , dont les sommes ⅙(b-u) , dont les sommes ⅙(b-u)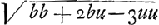 Ga naar voetnoot7) et ⅙(b+u) Ga naar voetnoot7) et ⅙(b+u)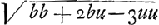 Ga naar voetnoot8) fournissent les valeurs des espaces DCF et KCFEL. Si l'on fait u=0, on trouve que ces espaces qui sont alors DCAD et KCAFEL sont égaux chacun à ⅙ bb. Je vous prie de vous ressouvenir de m'envoyer l'inverse des tangentes de NeutonGa naar voetnoot9), et de me croire toujours avec verité, Monsieur vôtre treshumble et tres obeissant serviteur Ga naar voetnoot8) fournissent les valeurs des espaces DCF et KCFEL. Si l'on fait u=0, on trouve que ces espaces qui sont alors DCAD et KCAFEL sont égaux chacun à ⅙ bb. Je vous prie de vous ressouvenir de m'envoyer l'inverse des tangentes de NeutonGa naar voetnoot9), et de me croire toujours avec verité, Monsieur vôtre treshumble et tres obeissant serviteur
Le M. de l'Hospital. | |
[pagina 567]
| |
Je n'ai receu vôtre lettre que depuis trois jours dont la raison est mon eloignement de ParisGa naar voetnoot8). |
|