Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–
[pagina 675]
| |||||||||
No 2876.
| |||||||||
[pagina 676]
| |||||||||
Mons. OldenbourgGa naar voetnoot7). Et j'en ay donné le moyen depuis quelque temps dans les Actes de LeipzigGa naar voetnoot8), d'une maniere assez aisée et tres universelle. Il est raisonnable de se servir de cette Hypothese, que les courbures sont comme les forces qui les produisent, pour avoir quelque chose d'arresté; mais si cela a assez lieu en effect, c'est ce que je ne voy pas encor bien clairement. Et on se peut figurer des constitutions des corps ou il n'en iroit pas ainsi. C'est ce qui m'a rebuté de cette recherche. Voyant que ma santé commence à chanceler, j'ay bien de la peine à me resoudre à des meditations qui ne servent qu'à exercer l'esprit. Je n'ay pas meme examinè la construction de ma paracentrique isochrone donnée par M. Bernoulli, m'estant contentè de donner mon analyse, qui est assez naturelle, avec ma construction qui n'a besoin que de la rectification d'une courbe ordinaireGa naar voetnoot9). Je suis de vostre sentiment, Monsieur, en ce que vous croyés que le probleme n'est pas encor bien resolu, lors qu'on ne fait que le reduire à quelque quadrature. Ainsi la courbe dont la rectification est employée par M. Bernoulli à la construction de la paracentrique n'estant pas assés construite encor elle même, est peu propre à la fin qu'il se propose. Mais je ne l'en reprends point. Est aliquid prodire tenus. Cependant je suis d'accord avec M. BernoulliGa naar voetnoot10), que c'est tousjours beaucoup quand un probleme est reduit aux quadratures. C'est à mon avis un grand et necessaire acheminement à sa veritable solution. Il y a plusieurs degrés dans les solutions; la plus parfaite sans doute est celle qui reduit les transcendentes à l'aire du cercle ou de l'Hyperbole. Au défaut de cela je voudrois pouuoir décrire la ligne transcendente per puncta à l'imitation de la Logarithmique qui se décrit par les moyennes proportionelles. Et quand cela manque encor, je me contente d'obtenir mon but per rectificationes linearum. Mais il y a des cas si difficiles, ou tout ce que j'y puis jusqu'icy, est de donner seriem infinitam. Je ne doute point qu'on ne trouue un jour la methode de reduire le tout aux plus simples quadratures possibles. Je croy même d'en voir les moyens, dont j'ay aussi des echantillons, mais je ne suis pas en estat d'y travailler. | |||||||||
[pagina 677]
| |||||||||
Si M. Bernoulli a bien determiné l'arc du ressort ou les tangentes des extremités sont paralleles, il me semble qu'il aura aussi les cas, ou ces tangentes sont convergentes au dessus ou au dessous de la corde, car il n'aura qu'a continuer la courbe ou en prendre la partie, puisque la partie du ressort bandé est encor un ressort bandé, en quelque endroit qu'on l'attache ou qu'on en prenne les extremitésGa naar voetnoot11). Cela fait voir encor que l'arc peut n'estre pas ambidextre, lors qu'en le bandant on pousse inégalement les extremités. Je suis aussi en doute sur ce quil dit de la voile, et la chose merite d'estre approfondie. Je crois que ma construction comprend toutes les isochrones paracentriques, tant celles de Mr. Bernoulli que celles que vous avés profondement consideréesGa naar voetnoot12) mais ie ne suis pas en estat ny en humeur de venir au detail. Pour ce qui est du calcul des differentio-differentielles, sur lequel vous desirés d'estre eclairci, je suis bien aise de pouvoir satisfaire à vos ordres en quelque chose. Ce n'est que trop souuent que je voy qu'on est obligé d'y venir: mêmes la recherche de la chainette y mene naturellement; mais c'est par une faveur speciale qu'on y peut s'en deliurer. Mes series infinies ont cela d'avantageux qu'elles resolvent les differentio-differentielles, de quelque degré qu'elles soyent, aussi aisement que les differences premieres. Comme les equations differentielles du premier degré sont pour l'inverse des tangentes, lors qu'on determine la courbe ex data proprietate tangentium, je trouue que celles des autres degrés peuuent venir lors que la courbe est determinée per proprietatem curvedinum seu linearum osculantium; ou bien par le melange des sommes parmy les differences. Car pour se deliurer des sommes, on descend à des differences plus profondes, tout comme pour se delivrer des racines on monte à des puissances plus hautes. Voicy un Exemple aisé pour les differences secondes pro linea sinuum, ç'est-à-dire lors que les arcs de cercle étendus en ligne droite estant les ordonnées, les sinus sont les abscisses. Soit l'arc y, le sinus de complement soit x, le rayon a, l'arc y sera egal
| |||||||||
[pagina 678]
| |||||||||
√(aa-xx) dy (3)=adx. Pour abreger faisons 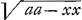 (4)=v, et il y aura vdy(5)=adx, et rursus ipsam aeq. 5. differentiando vddy+dvdy(6)=addx. Et si nous faisons que les arcs y croissent uniformement, c'est-à-dire si dy est constante ou ddy=0 (7), au lieu de 6 il y aura dvdy (8)=addx. Differentiando aeq. 4 il y aura dv(9)=-xdx/v car vv=aa-xx, donc vdv=-xdx. Et (par 5 et 9) dv (10)=-xdy/a donc par 8 et 10 il y aura -xdydy (11)=aaddx. Ce qui fait voir que les arcs de cercle croissant uniformement, les sinus de complement décroissent de telle sorte qu'ils sont proportionels à leur propres differences secondes; au lieu que lors que les Logarithmes croissent uniformement les nombres sont proportionels à leur propres differences premieres. Soit x(12)==a+byy+cy4+ey6 etc., et (posito ddy=o ut dictum) ddx sera (13)=dydy multiplié par 1. 2. b+3. 4. cyy+5. 6. ey4 etc., et l'equation 11 ou xdydy++aaddx (14)=0 estant interpretée par 12 et 13 il y aura: (4)=v, et il y aura vdy(5)=adx, et rursus ipsam aeq. 5. differentiando vddy+dvdy(6)=addx. Et si nous faisons que les arcs y croissent uniformement, c'est-à-dire si dy est constante ou ddy=0 (7), au lieu de 6 il y aura dvdy (8)=addx. Differentiando aeq. 4 il y aura dv(9)=-xdx/v car vv=aa-xx, donc vdv=-xdx. Et (par 5 et 9) dv (10)=-xdy/a donc par 8 et 10 il y aura -xdydy (11)=aaddx. Ce qui fait voir que les arcs de cercle croissant uniformement, les sinus de complement décroissent de telle sorte qu'ils sont proportionels à leur propres differences secondes; au lieu que lors que les Logarithmes croissent uniformement les nombres sont proportionels à leur propres differences premieres. Soit x(12)==a+byy+cy4+ey6 etc., et (posito ddy=o ut dictum) ddx sera (13)=dydy multiplié par 1. 2. b+3. 4. cyy+5. 6. ey4 etc., et l'equation 11 ou xdydy++aaddx (14)=0 estant interpretée par 12 et 13 il y aura:
Donc, destruisant tous les termes, pour faire que cette equation soit identique, il y aura a+1. 2. baa=0, et b+3. 4. caa=0 et c+5. 6. eaaGa naar voetnoot14) =0. C'est-à-dire b=-1/1. 2. a, et c=-b/3. 4. aa, ou bien c=1/1. 2. 3. 4. a3 et e=--1/1. 2. 3. 4. 5. 6. a5 et ainsi de suite; donc par 12 nous aurons x (16)==1/1a-1/1. 2. a yy+1/1. 2. 3. 4. a3 y4-1/1. 2. 3. 4. 5. 6. a5 y6 etc. ce qui donne la valeur du sinus de complement x par l'arc y et par le rayon a. On trouueroit la même chose par l'equation 3. en ostant l'irrtationelle et faisant aadydy (17)==xxdydy+aadxdx, mais non pas si aisement. Il y a encor d'autres abregés que j'explique dans les ActesGa naar voetnoot15). Mais pour vous donner un exemple d'un probleme Geometrique, prenons celui de la Chainette: et je vous donneray en meme temps l'analyse dont je me | |||||||||
[pagina 679]
| |||||||||
suis servi autres fois pour le resoudre, puisque vous avés temoigné de la desirer
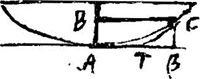 aussiGa naar voetnoot16). Soit AB,x; BC,y; AT, retranchée par la tangente, est la distance entre l'axe et le centre de gravité de l'arc AC. Or, Cβ ou AB est à Tβ, comme dx à dy; donc Tβ sera x 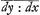 , et AT sera y-x. , et AT sera y-x. 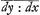 . L'arc AC soit appellé c et par la nature du centre de gravité il est manifeste, qu' AT sera . L'arc AC soit appellé c et par la nature du centre de gravité il est manifeste, qu' AT sera 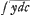 : c(1)=y-xdy:dx ou bien ∫ydc(2)=cy-cxdy:dx; et differentiando ydc(3)=cdy+ydc- : c(1)=y-xdy:dx ou bien ∫ydc(2)=cy-cxdy:dx; et differentiando ydc(3)=cdy+ydc-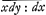 dc--cdy-cxd, dc--cdy-cxd, 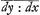 . Et rejettant ce qui se détruit, il y aura dc . Et rejettant ce qui se détruit, il y aura dc 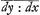 +cd, +cd,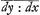 (4)=0. Supposons que les y ou (4)=0. Supposons que les y ou 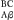 croissent uniformement,
ou que dy soit constante et ddy (5)=0, nous aurons d. croissent uniformement,
ou que dy soit constante et ddy (5)=0, nous aurons d. 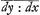 (6)=--dy ddx: (6)=--dy ddx: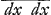 , et au lieu de 4 il y aura dcdx-cddx (7)=0, c'est-à-dire summando dx:c(8)=dy:a (car cette equ. 8. estant differentiée rend l'equation 7) ou bien adx (9)=cdy et differentiando addx(10)=dcdy. Or generalement en toute courbe dcdc (11)=dydy+dxdx et differentiando dc ddc=dyddy++dxddx, donc icy (par 5) dcddc (12)=dxddx, et (par 10 et 12) addc (13)==dxdy et summando adc(14)=xdy+bdy. Soit x+b (15)=z, fiet dx (16)=dz et adc=zdy, et (par 11 et 16) dcdc=dzdz (17)+dydy. Donc par 14, 15, 17, nous aurons aadzdz+aadydy (18)=zzdydy, et enfin y(19)=aa , et au lieu de 4 il y aura dcdx-cddx (7)=0, c'est-à-dire summando dx:c(8)=dy:a (car cette equ. 8. estant differentiée rend l'equation 7) ou bien adx (9)=cdy et differentiando addx(10)=dcdy. Or generalement en toute courbe dcdc (11)=dydy+dxdx et differentiando dc ddc=dyddy++dxddx, donc icy (par 5) dcddc (12)=dxddx, et (par 10 et 12) addc (13)==dxdy et summando adc(14)=xdy+bdy. Soit x+b (15)=z, fiet dx (16)=dz et adc=zdy, et (par 11 et 16) dcdc=dzdz (17)+dydy. Donc par 14, 15, 17, nous aurons aadzdz+aadydy (18)=zzdydy, et enfin y(19)=aa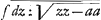 , c'est-à-dire il ne faut que chercher la quadrature d'une figure, dont l'ordonnée est aa:√zz-aaGa naar voetnoot17). On peut faire b=a ou -a, ou bien de quelque autre grandeur qu'on voudra, comme il depend aussi de nous d'augmenter ou diminuer y par une droite constante et d'écrire , c'est-à-dire il ne faut que chercher la quadrature d'une figure, dont l'ordonnée est aa:√zz-aaGa naar voetnoot17). On peut faire b=a ou -a, ou bien de quelque autre grandeur qu'on voudra, comme il depend aussi de nous d'augmenter ou diminuer y par une droite constante et d'écrire
y+c (20)=aa 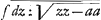 .
Pour ce qui est des equations exponentielles, je vous diray Monsieur, que toutes les fois que le probleme se reduit à des exponentielles traitables, il est resolu en perfection, et il n'y a plus rien à chercher. De sorte; que c'est proprement le plus haut point de la Geometrie des Transcendentes. Pour vous en developper tout le mystere soit par exemple .
Pour ce qui est des equations exponentielles, je vous diray Monsieur, que toutes les fois que le probleme se reduit à des exponentielles traitables, il est resolu en perfection, et il n'y a plus rien à chercher. De sorte; que c'est proprement le plus haut point de la Geometrie des Transcendentes. Pour vous en developper tout le mystere soit par exemple 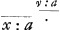 =y:a ou bien posant a pour l'unité, soit =y:a ou bien posant a pour l'unité, soit
| |||||||||
[pagina 680]
| |||||||||
xv=y; c'est comme si je disois qu'v est à l'unité comme le logarithme de la grandeur y est au Logarithme de la grandeur x. Ainsi supposé que la valeur d'v soit donnée par x ou par y, ou par toutes les deux, la ligne se peut construire Geometriquement par points aussi bien que la logarithmique meme, et on en peut donner de meme la tangente et les autres proprietés. Et je puis tousjours changer l'equation exponentielle en differentielle, mais non pas vice versa, car, puisque xv (1)=y donc v log. x (2)=log. y, ou bien v 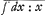 (3)= (3)=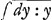 et differentiando vdx:x+dv et differentiando vdx:x+dv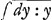 dx:x (4)=dy:y. Si v estoit egal à x, alors dy seroit à dx, ou bien, l'ordonnée seroit à la soutangentielle, comme y multipliée par 1+log. x, est à l'unité, c'est-à-dire la soutangentielle sera egale à l'unité multipliéeGa naar voetnoot18) par 1+log. x. Si nous posons que les x croissent uniformement, il y aura yydxdx+axyddy=axdydyGa naar voetnoot19), et cette equation differentio-differentielle se peut reduire à l'exponentielle xx=y, qui en donne la construction. Ainsi bien loin qu'on doive croire que ces exponentielles sont embarassées, il faut juger que de toutes les expressions qui enseignent la construction des lignes Transcendentes par des points determinables suivant la Geometrie ordinaire, ce sont les plus simples. Et il faut considerer que les exponentielles n'employent point d'autre grandeur qu'x et y, etc., c'est à dire que des grandeurs ordinaires, au lieu que les differentielles employent encor d'extra-ordinaires, comme dx, ddx etc., ce qui les empeche de servir aux determinations des intersections des courbes ou aux equations locales. car si j'avois dy:dx (1)=x:a pour une courbe, scavoir pour la Logarithmique; et xx+yy (2)=aa pour l'autre, scavoir pour le cercle, qui me donne xdx+ydy(3)=0, ou dy:dx(4)=-x:y, il m'est point permis de me servir des equations 3 ou 4 pour le cas de rencontre des courbes, ny d'oster dy:dx par le moyen des equations 1 et 4, bien que je sçache que les courbes des equations 1 et 2, scavoir la logarithmique et le cercle, se rencontrent; excepté le cas ou leur rencontre est un attouchement. Car sans cela, quoyque x et y soyent les mesmes dans les deux courbes, dx et dy ne le sont point (mais ddx, ddy ne sont les memes de part et d'autre, que dans le cas de l'osculation des deux
courbes qui est un attouchement plus parfait). Au lieu que les exponentielles ne contenant qu'x et y, qui sont les memes en cas de rencontre, servent absolument à la détermination des intersections. Ainsi c'est par elles ou leur semblables qu'on acheve la recherche et qu'on peut oster une inconnue. Je trouue ces equations encor utiles dans les nombres. Je tascheray de me faire entendre dans le traité que je projette pour mon nouueau calcul, et vous serés obligé de ce que vous y voudrés contribuer. Nous verrons ce que feront M. le Marquis de l'Hospital et Messieurs Bernoulli. dx:x (4)=dy:y. Si v estoit egal à x, alors dy seroit à dx, ou bien, l'ordonnée seroit à la soutangentielle, comme y multipliée par 1+log. x, est à l'unité, c'est-à-dire la soutangentielle sera egale à l'unité multipliéeGa naar voetnoot18) par 1+log. x. Si nous posons que les x croissent uniformement, il y aura yydxdx+axyddy=axdydyGa naar voetnoot19), et cette equation differentio-differentielle se peut reduire à l'exponentielle xx=y, qui en donne la construction. Ainsi bien loin qu'on doive croire que ces exponentielles sont embarassées, il faut juger que de toutes les expressions qui enseignent la construction des lignes Transcendentes par des points determinables suivant la Geometrie ordinaire, ce sont les plus simples. Et il faut considerer que les exponentielles n'employent point d'autre grandeur qu'x et y, etc., c'est à dire que des grandeurs ordinaires, au lieu que les differentielles employent encor d'extra-ordinaires, comme dx, ddx etc., ce qui les empeche de servir aux determinations des intersections des courbes ou aux equations locales. car si j'avois dy:dx (1)=x:a pour une courbe, scavoir pour la Logarithmique; et xx+yy (2)=aa pour l'autre, scavoir pour le cercle, qui me donne xdx+ydy(3)=0, ou dy:dx(4)=-x:y, il m'est point permis de me servir des equations 3 ou 4 pour le cas de rencontre des courbes, ny d'oster dy:dx par le moyen des equations 1 et 4, bien que je sçache que les courbes des equations 1 et 2, scavoir la logarithmique et le cercle, se rencontrent; excepté le cas ou leur rencontre est un attouchement. Car sans cela, quoyque x et y soyent les mesmes dans les deux courbes, dx et dy ne le sont point (mais ddx, ddy ne sont les memes de part et d'autre, que dans le cas de l'osculation des deux
courbes qui est un attouchement plus parfait). Au lieu que les exponentielles ne contenant qu'x et y, qui sont les memes en cas de rencontre, servent absolument à la détermination des intersections. Ainsi c'est par elles ou leur semblables qu'on acheve la recherche et qu'on peut oster une inconnue. Je trouue ces equations encor utiles dans les nombres. Je tascheray de me faire entendre dans le traité que je projette pour mon nouueau calcul, et vous serés obligé de ce que vous y voudrés contribuer. Nous verrons ce que feront M. le Marquis de l'Hospital et Messieurs Bernoulli.
| |||||||||
[pagina 681]
| |||||||||
Vostre explication de la pesanteur paroist jusqu'icy la plus plausible. Il seroit seulement à desirer qu'on pût rendre raison pourquoy celle qui paroist dans les Astres est en raison doublée reciproque des distances. Comme je vous disois un jour à Paris qu'on avoit de la peine à connoistre le veritable sujet du Mouuement, vous me répondîtes que cela se pouuoit par le moyen du mouuement circulaire, cela m'arresta; et je m'en souuins en lisant à peu près la même chose dans le liure de Mons. Newton; mais ce fut lorsque je croyois déja voir que le Mouuement circulaire n'a point de privilege en cela. Et je voy que vous estes dans le meme sentiment. Je tiens donc que toutes les hypotheses sont equivalentes et lors que j'assigne certains mouuemens à certains corps, je n'en ay ny puis avoir d'autre raison, que la simplicité de l'Hypothese croyant qu'on peut tenir la plus simple (tout consideré) pour la veritable. Ainsi n'en ayant point d'autre marque, je crois que la difference entre nous, n'est que dans la maniere de parler, que je tache d'accommoder à l'usage commun, autant que je puis, salva veritate. Je ne suis pas meme fort eloigné de la vostre, et dans un petit papierGa naar voetnoot20) que je communiquay à Mr. Viviani, et qui me paroissoit propre à persuader Messieurs de Rome à permettre l'opinion de Copernic, je m'en accommodois. Cependant si vous estes dans ces sentimens sur la realité du mouuement, je m'imagine que vous deuriés en avoir sur la nature du corps de differens de ceux qu'on a coustume d'avoir. J'en ay d'assez singuliers et qui me paroissent demonstrés. Je souhaiterois d'apprendre un jour vos reflexions que vous m'aviés fait esperer tant sur mes animadversions in CartesiumGa naar voetnoot21), que sur ce que je vous avois écrit contre le vuide et les AtomesGa naar voetnoot22). Je veux lire avec attention la Theorie du manoeuvre et vous remercie cependant des communications de vostre remarque qui paroist de consequence. Il y a dejà du temps que j'ay envoyé à Leipzig mes reflexions sur l'Isochrone du Professeur BernoulliGa naar voetnoot23); en y envoyant vostre construction du probleme du MedecinGa naar voetnoot24), j'y adjouteray quelque chose de vos considerationsGa naar voetnoot25) sur ce que le Professeur vient de donner. Mr. Tayler s'est excusé de venir à WolfenbutelGa naar voetnoot26). N'a-t-on point des nouuelles de la restitution entiere de Mr. Newton?Ga naar voetnoot27) Je la souhaitte fort. Quelques | |||||||||
[pagina 682]
| |||||||||
uns ayant vû des definitions que j'ay données dans la preface de mon Code DiplomatiqueGa naar voetnoot28) (dont, pour le dire en passant, je vous feray remettre un exemplaire) m'ont exhorté de mettre en ordre un amas d'autres que j'ay fabriquées autres fois. Voicy celles de la preface que je soûmets à vostre jugement. Je dis que la justice est une charité conforme à la sagesse. La sagesse est la science de la felicité. la charite est une bienveuillance generale. La bienveuillance est habitus diligendi. Diligere, aimer, cherir (en nostre sens) est se faire un plaisir de la felicité d'autruy. Vous ne pouués manquer, Monsieur, d'avoir mille belles meditations encor hors des mathematiques. Il ne faudrait pas nous en priver. Je me souuiens qu'un jour vous me fistes esperer quelque chose de cette natureGa naar voetnoot29). N'aurons nous pas bien tost vostre Dioptrique? J'espere d'y trouuer des explications des meteores emphatiquesGa naar voetnoot30), suivant cet echantillon qu'on a vû de vous autres fois dans le journal des scavansGa naar voetnoot31). Vostre crystal d'Islande ne vous at-il donne aucun phenomene singulier sur les couleurs? Il semble qu'il y deuroit encor seruir. Vous aviés aussi fait ce me semble quelques decouuertes sur la force electriqueGa naar voetnoot32). Que jugés vous Monsieur de l'Hypothese de Monsieur Halley, sur le noyau mobile contenu dans le globe de la terre, pour expliquer la variation de l'aimant?Ga naar voetnoot33) Et sur ce que Mr. Newton croit avoir rendu raison du flus et reflus de la merGa naar voetnoot34). Nous attendons aussi l'explication de vostre ligne propre pour les pendules des vaisseauxGa naar voetnoot35). Je suis avec zele Monsieur Vostre treshumble et tresobeissant serviteur Leibniz. | |||||||||
[pagina 683]
| |||||||||
P.S. Si je suppose que la voile ne s'etend ou ne s'allonge point et prends
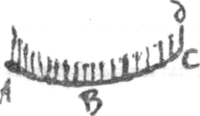 l'effect du vent pour ce qui se feroit si un filet ABC consideré comme sans pesanteur en luy même, estoit chargé par tout d'un poids égal, tel que CD; le calcul qui me vient tout presentement, me donne une ligne, dont la construction demande une quadrature, qu'il est en mon pouvoir de donner autant qu'il est possible, et qui se reduira (: autant que je puis juger par avance :) à celle de l'hyperbole. Mais je crois que ce sera autrement que lors qu'on construit la chainetteGa naar voetnoot36). |
|

