Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 673]

N^o 2875.
Christiaan Huygens aux Editeurs des ‘Acta Eruditorum’.
[août 1694].
Appendice II au No. 2873.

La minute se trouve à Leiden, coll. Huygens¹⁾.
La pièce a été publiée dans les Acta Eruditorum de septembre 1694, p. 338 et 339²⁾.

C.H.Z. Constructio universalis Problematis a Clarissimo Viro, Jo. Bernoulio, superiori anno mense Majo propositi.

Cum in Actis Lipsiensibus Constructionem hanc me reperisse significarem, mense Octobri A.^o 1693³⁾, edenda tamen ea supersedi, quod futurum putabam, ut vel ab Auctore ipso vel Clar.^o Viro fratre ejus, vel alio quopiam, haud multum absimilis brevi in lucem prodiret, ac subverebar etiam ne actum agerem. Quoniam vero nusquam adhuc comparuit, & est inter eas quae dari possint quodammodo



simplicissima; non videtur absque ea diutius relinquendum tam eximium problema. Est autem hujusmodi⁴⁾. Sit in recta AB datum punctum A, et oporteat

1) Elle y fait suite à celle du N^o. 2873.

2) Nous imprimons d'après la minute. Le texte des Acta en diffère en plusieurs endroits par un autre choix des mots, qui peut être le fait de la rédaction, et contient de plus quelques erreurs importantes du copiste ou du typographe. La figure, au contraire, y est beaucoup plus exactement construite.

3) Voir la pièce N^o. 2823 à la page 513.

4) La construction qui va suivre est presque identique avec celle que l'on trouve dans la Lettre N^o. 2828 aux pages 535 et 536. On peut donc consulter les notes de cette lettre qui s'y rapportent.

[p. 674]

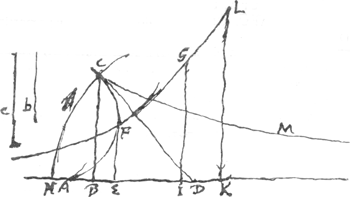
invenire curvam AFC ejusmodi ut tangens ejus quaevis CD abscindat ab recta AB portionem AD, quae ad ipsam CD habeat rationem datam lineae c ad b.

Constructio: sicut c ad b, ita quaelibet AE in recta AB assumpta ad EF ipsi perpend. et per F punctum ponatur descripta Logarithmica quaecunque cujus asymptotos sit AB, ad quam descendat illa versus A. Deinde ab A versus E accepta distantia qualibet AD, sit ut c ad b hoc est ut AE ad EF, ita AD ad aliam DH et ea tanquam radio, et centro D describatur circuli circumfer. HC. ac praeterea applicetur ad Logarithmicam recta IG asymptoto perpendicularis, ipsique DH aequalis. Jam ut b ad duplum c; ita fiat IE ad EK, sumendam in asymptoto in partem alterutram, nihil enim refert⁵⁾, et applicetur rursus ad logarithmicam recta KL; utque summa duarum KL, EF ad earum differentiam, ita sit DH ad DB; quae sumenda versus A punctum si AD major sit quam AE; at in contrariam, si minor. Jam recta BC ad asymptoton perpendicularis secabit circumferentiam HC in puncto C, quod erit in curva quaesita AFC. Tangit autem hanc rectam EF in F punctum.

Est porro animadversione dignum, non simplicem esse curvaturam lineae hujus cum c major est quam b, sed ex duabus eam tunc componi, ex uno quodam puncto exeuntibus⁶⁾, ut CFA, CM⁷⁾. In puncto autem extremo C, recta ex A educta occurrit curvis AFC, CM ad angulos rectos⁸⁾, ac proportionales sunt DA, DC, DB.

5) Comparez la note 8 de la Lettre N^o. 2828; c'est ici la seule modification réelle de la construction formulée dans la Lettre N^o. 2828.

6) Voir, à propos du point de rebroussement C, la note 17 de la Lettre N^o. 2819, la Lettre N^o. 2828 à la page 536, celle N^o. 2833 à la page 552, et la pièce N^o. 2834.

7) Le texte des Acta ajoute: quarum haec in infinitum progreditur.

8) On ne retrouve pas cette remarque dans la correspondance. Il s'agit d'ailleurs d'une conséquence immédiate de la proportion: DC:DB=c:b=DA:DC, indiquée entre autres dans la Lettre N^o. 2833, p. 552.