Oeuvres complètes. Tome X. Correspondance 1691-1695

N^o 2873.
Christiaan Huygens à G.W. Leibniz.
24 août 1694.

La minute¹⁾ se trouve à Leiden, coll. Huygens.
La minute a été publiée par P.J. Uylenbroek²⁾, la lettre par C.I. Gerhardt³⁾.
La lettre est la réponse aux Nos. 2863, 2866 et 2871.
G.W. Leibniz y répondit par le No. 2876.

Sommaire:⁴⁾
Que j'avois le mois de Juin. Je voudrois un exemple des differentiodifferentieles. de la valeur je doute. les 2 sautes aux Acta. Extrait de Wallis. Ma replique a Renau. Comment il s'est souvenu de mon ancien sentiment sur le mouvt. circulaire, que je l'ay corrigè. De longtemps rien du Marquis. Bernoulli triomphe et vous brave. vous vous avez attiré [motsillisibles] mais de peu d'utilitè. Peut estre on peut construire plus simplement. Vous le surpassez pour la construction. il y a tant d'autres cas. Je crois qu'il emploie bien le principe du ressort, en considerant la courbure en raison contraire de la force, quoyque cela se fasse par condensation en partie. Resteroit a vous proprie dictus et ces autres cas. Je veux croire qu'il demontre bien sa paracentrique, ce que je ne scay comment il a pu rencontrer. Je seray saschè d'emploier tant de temps à ces choses. La forme du sac est tres subtilement trouvée, et il est admirable que cette identitè de courbes se rencontre. J'aurois cru n'avoir rien a moins sans reduire aux quadratures du cercle ou de l'hyperbole. toutefois on ne laisse pas de trouver des proprietes considerables de ces courbes. Vous pouvez faire mention de mes pensees dans ce que vous envoierez pour les Acta. ferez bien de le reprendre sur l'indice des constructions par l'hyperhole que je suis autant pour le cercle en cecy.

A la Haye ce 24 Aoust 1694.

Monsieur

J'avois receu les Acta de Leipsich jusqu'au mois de Juin, il y avoit 8 jours, lorsqu'arriva l'Extrait que vous m'avez fait la faveur de m'envoier⁵⁾, dont je ne

1) Elle ne diffère pas sensiblement de la lettre qui se trouve à Hannover.

2) Chr. Hugenii etc. Exercitationes Mathematicae, Fasc. I, p. 195.

3) Leibnizens Mathematische Schristen, Band II, p. 189, Brieswechsel, p. 743.
Une traduction latine fragmentaire de la lettre parut dans les ‘Acta Eruditorum’ de septembre. Comme elle est incomplète et assez libre, nous la reproduisons, avec les remarques que Leibniz y a ajoutées, comme Appendice à cette lettre.

4) Ce sommaire, biffé par Huygens, probablement à mesure qu'il avait traité dans sa lettre le sujet indiqué, est à peine lisible. Nous en reproduisons ce que nous avons pu déchiffrer.

5) Avec la Lettre N^o. 2871.

[p. 665]

laisse pas de vous estre obligè. Il semble que mesme chez vous ces nouvelles ne se debitent que bien tard. Je trouve le travail triennal de Mr. Bernoully bien considerable, pourvu que tout ce qu'il avance soit vray; aussi s'en glorifie-t-il beaucoup⁶⁾. Pour le principe du ressort, je crois qu'il l'a bien emploiè, et qu'il est vray que les raions qui mesurent la courbure sont en raison contraire des forces qui font plier⁷⁾ le ressort, quoyque, selon moy, ce ne soit pas seulement la surface exterieure qui s'etend mais l'interieure en mesme temps s'accourcit⁸⁾, l'acier ou matiere pliante se condensant d'un costè et comme rentrant en elle mesme, pendant que de l'autre elle se dilate. Si ce principe n'estoit pas le veritable et l'unique mais que la ligne AFC⁹⁾ fust une courbe dependante d'infinies experiences, je trouverois toute sa recherche fort vague et peu digne qu'on s'y amusast. Et mesme à cette heure tout ce qu'il a trouvè ne me paroit d'aucune utilitè, mais seulement des exercitations fort belles et subtiles, lors qu'on ne trouve pas de quoy emploier les mathematiques avec plus de fruit.

C'est une etrange supposition de prendre les quadratures de toute courbe

6) Allusion au début du premier des articles mentionnés dans la note 3 de la Lettre N^o. 2871, où il dit: ‘Post triennale silentium promissi tandem fidem libero, sed ita, ut moram quam Lector alias inique ferre posset, nonnullo foenore compensum, dum Elaterum curvatorum non in una sola, (ut initio fueram pollicitus), sed generaliter in quacunque Extensionum hypothesi constructam exhibeo; quod primus ni fallor exequor, postquam a multis inutiliter tentatum Problema fuisset’.

7) La minute a: ‘qui agissent a faire plier’.

8) Dans l'article intitulé ‘Jac. B. Explicationes, annotationes et additiones ad ea, quae in Actis sup. anni de Curva Elastica, Isochrona et Paracentrica, & Velaria, hinc inde memorata, & partim controversa leguntur; ubi de Linea mediarum directionum aliisque novis’, qui parut dans les ‘Acta’ de déc. 1695, Jacques Bernoulli reconnaît la justesse de cette remarque, qu'il connaissait par la traduction latine, notre N^o. 2874, de la présente lettre. En conséquence il modifie sa construction, en remarquant toutefois qu'il avait emprunté le principe erroné en question à l'article de Leibniz, cité dans la note 6 de la Lettre N^o. 2871, tout en doutant de sa justesse: ‘propterea quia quicquid extensionis, etiam compressionis capax esse debet’.

9) Une grande partie de l'article de Bernoulli, mentionné dans la note 6, est consacrée à la construction de la courbe élastique dans la supposition que ce que Bernoulli appelle la ‘tensio’, au lieu d'être proportionnelle aux ‘vires tendentes’ en est une fonction quelconque définie par cette ligne AFC, qu'il nomme: ‘Linea Tensionum’. Ajoutons que, d'après la manière donc la ‘Linea Tensionum’ est employée par Bernoulli dans sa construction, la ‘tensio’ représente en chaque point de la courbe élastique la flexion locale, réciproquement proportionnelle au rayon de courbure, et les ‘vires tendentes’ le moment, par rapport au même point, de la force fléchissante appliquée à l'extrémité du ressort; d'où il suit que dans le cas de la proportionnalité de la ‘tensio’ et des ‘vires tendentes’ le rayon de courbure est ‘en raison contraire’ du moment ‘des forces qui font plier le ressort’, conformément au principe que Huygens considère comme ‘le véritable et l'unique’.

[p. 666]

comme estant données¹⁰⁾, et quand la construction d'un probleme aboutist à cela, hors mis que ce ne soit la quadrature de l'hyperbole ou du cercle, j'aurois cru n'avoir rien fait, par ce que mesme mechaniquement on ne scauroit rien effectuer. Il vaut un peu mieux de supposer qu'on peut mesurer toute ligne courbe, comme je vois aussi que c'est vostre sentiment¹¹⁾. Je trouve au reste que Mr. Bernoulli n'a determiné que la courbure de l'arc A, où les tangentes des extremités E, F sont



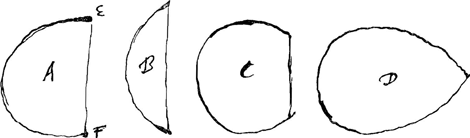paralleles, les quelles je considere conjointes par la corde EF. Il resteroit à donner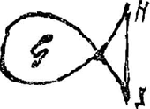



la figure du veritable arc B; item de C dont les extrem ités vont en s'approchant; de D, où elles s'assemblent, et de G où elles passent au delà et sont retenues par un baston HI¹²⁾. Ce qu'il dit de la voile pressée par une liqueur, qui luy donneroit la mesme courbure que du ressort C, est encore bien subtilement trouvé, s'il est veritable¹³⁾. Mais jusques à ce que je voie les demonstrations, je me defie un peu des Theoremes de Mr. Bernoulli, depuis que

10) La construction générale de Bernoulli de la courbe élastique dépend de la quadrature de la ‘Linea Tensionum’ et de celle d'une autre courbe, construite au moyen de cette première quadrature; sa construction particulière, pour le cas de la proportionnalité de la ‘tensio’ et des ‘vires tendentes’, de celle de la courbe Dans l'articlecité dans la note 8, de décembre 1695, Jacques Bernoulli motive, à la page 543, l'emploi qu'il fait des quadratures.

11) Voir la Lettre N^o. 2829 à la page 541 et la Lettre N^o. 2871 à la page 662.

12) En réponse à cette remarque, Jacques Bernoulli, dans l'article cité dans la note 8, renvoie d'abord au Scholium 5 de son premier article sur la courbe élastique (voir la note 3 de la Lettre N^o. 2871), où on lit en effet: ‘Si directio ponderis vel cujusvis potentiae inflectentis, ad Laminam, ejusve tangentem in puncto appensionis sit obliqua, nascetur curva paululum diversa ab AQR’ [l'arc A de la présente lettre], ‘quam tamen eadem facilitate determinare possum. Sed nolo nimium evagari’. Ensuite il montre la quadrature un peu plus compliquée à laquelle le problème se réduit dans cette supposition plus générale au cas de la proportionnalité de la ‘tensio’ aux ‘vires tendentes’.

13) Au passage que Huygens a en vue, Jacques Bernoulli identifie la courbe élastique avec celle formée par une voile remplie de liquide et étendue entre deux droites parallèles. Et il le fait à raison, puisque dans les deux cas le rayon de courbure doit être partout réciproquement proportionnel à la distance à une droite fixe, c'est-à-dire, dans le cas de la voile, à celle du niveau du liquide, la pression du liquide étant proportionnelle à cette distance, et dans celui de la courbe élastique à celle dans laquelle agit la force fléchissante.

[p. 667]

j'ay vu qu'il se trompe et se retracte quelques-fois, comme en ce qu'il avoit assurè cy-devant que la voile tendue par le vent se plioit en arc de cercle, et, en quelques cas, moitié en cercle et moitié en courbe de la chaine¹⁴⁾. Je doute encore s'il est



bien vray que la voiliere soit la mesme que la Funicularia, comme les deux freres le croient maintenant, par ce que je puis demontrer¹⁵⁾ qu'une voile composée d'un nombre fini de pieces egales et droites, comme ABC, sera courbée autrement par le vent et autrement par son poids. Il faudroit donc que dans le nombre infini cette difference vint à rien¹⁶⁾.

Il semble que vous teniez pour veritable sa construction de vostre paracentrique¹⁷⁾, apres en avoir comme je crois¹⁸⁾ examinè sa demonstration, ce que je n'ay pas encore fait. C'est une rencontre assez etrange d'y avoir pu emploier sa courbe du ressort. Mais vostre construction sera assurement bien meilleure si vous n'avez besoin que de mesurer une courbe geometrique, ou de laquelle vous scachiez du moins trouuer les points¹⁹⁾. Lors qu'il dit qu'il n'y a qu'une seule courbe comme Αϰωη, qui fasse eloigner egalement le mobile du point A apres la

14) Voir la note 33 de la Lettre N^o. 2693. Plus tard, dans l'article de mai 1692 (voir la note 25 de la Lettre N^o. 2819), Jacques Bernoulli, après avoir annoncé que la partie AB de la voile était identique avec la chaînette, avait mitigé un peu son assertion étrange, en admettant qu'il y aurait sur la voile une partie intermédiaire, où elle prendrait une forme qui tiendrait à la fois de la nature de la chaînette et de celle du cercle. Or, dans sa réponse à la présente remarque, il proteste de ne s'être jamais contredit en principe, puisqu'il n'avait admis la forme circulaire que dans l'hypothèse que l'air ne trouverait pas d'occasion de s'échapper de la voile. Toutefois il assure maintenant que de fait la voile prendra la forme de la chaînette.

15) Voir la pièce N^o. 2835.

16) A cette remarque Bernoulli répondit, non sans raison: ‘Nec moror discrimen, quod fortasse intercederet, si velum ex numero finito rectarum compositum intelligeretur; cum nihil sit frequentius in natura, quam ut in casu infinite parvorum quantitatum differentia evanescat; nec magis hoc mirandum, quam miramur, quod evanescente base trianguli evanescit crurum differentia’.

17) Comparez la Lettre N^o. 2871, à la page 661, et consultez, sur la courbe en question, la Lettre N^o. 2841 aux pages 574 et 575 et surtout la note 22 de cette lettre.

18) Les mots ‘comme je crois’ manquent dans la minute.

19) Voir la Lettre N^o. 2871, vers la fin. Ajoutons que Bernoulli à ce propos renvoie à l'article cité dans la note 22 de la Lettre N^o. 2841, contenant sa première solution au moyen de la rectification de la courbe élastique, où il avait déjà annoncé qu'il possédait de même une solution dépendant de la quadrature d'une courbe algébrique, et à sa seconde solution de septembre 1694, citée dans la même note, où le problème est réduit à la rectification de la lemniscate, observant d'ailleurs que la courbe élastique était bien plus facile à construire que mainte courbe algébrique.

[p. 668]

chute par TA, je vois clairement qu'il se trompe²⁰⁾, et qu'il y a une infinité de telles courbes, comme sont Aβζ, Aδγ, jusqu'à la droite Aη inclusivement, quoyque



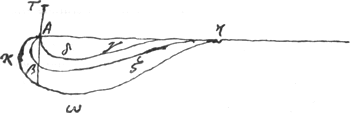je n'aye pas encore cherché comment il les faut decrire. Je vois aussi qu'il reste d'autres courbes à determiner en cette matiere, comme pour aprocher egalement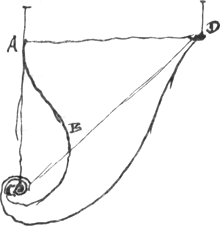



du point C en venant du point directement au dessus A, ou de D, qui est plus haut, et à costè aux quels cas les courbes ABC, DEC feront des tours infinis autour du point C²¹⁾, Voila encore bien d'exercice pour vostre calcul differentiel ou double differentiel, duquel je souhaite fort de voir une fois une exemple.

Vous ferez bien de reprendre Mr. Bernoulli sur l'indice des courbes constructibles par la quadrature de l'hyperbole²²⁾. Ce seroit vouloir l'impossible que de les vouloir reduire toutes à cela. Et pour moy j'estime qu'on a tout aussi bien reussi quand on aboutit à la mesure des arcs de cercle.

Je ne scay si vous aurez encore vu ma remarque²³⁾ sur la manoeuvre des

20) Dans sa réponse Jacques Bernoulli reconnaît cette erreur, s'excusant, entre autres, par la hâte avec laquelle il avait écrit son article. En effet, il n'avait étudié que le cas particulier où la tangente de la courbe en A est horizontale.

21) L'existence de ces courbes paracentriques isochrones à tours infinis a été niée par Jacques Bernoulli dans sa réponse et par Jean Bernoulli dans les ‘Acta’ de février 1695, à la page 65 de l'article: ‘Joh. Bernoulli, animadversio in praecedentem solutionem Illustris D. Marchionis Hospitalii’, etc. Toutefois Huygens avait parfaitement raison. Et pour s'en convaincre il suffit de considérer: 1^o. que, si v_o signifie la vitesse de départ au point D, le pôle C devra être atteint dans le temps fini CD: v_o, 2^o. que la vitesse d'arrivée au pôle étant égale à , où h=AC, l'angle de la vitesse avec le rayon vecteur devra s'approcher de plus en plus de la valeur: arc cos . La courbe, en s'approchant du centre, ressemblera donc de plus en plus à une spirale logarithmique et ne pourra y arriver qu'après un nombre infini de tours.

22) Voir la note 10 de la Lettre N^o. 2871.

23) Voir la pièce N^o. 2826.

[p. 669]

vaisseaux de Mr. Renaud. Mais quand vous ne l'auriez pas vue, vous ne laisserez pas de pouvoir juger de nostre different par ma replique²⁴⁾, que je vous envoie. Ce ne sont pas de petites bevues ou omissions, qui se rencontrent dans cet ouvrage imprimé de l'expres commandement du Roy (comme il y a au titre²⁵⁾) et examiné par Mrs. de l'Academie des Sciences, mais une erreur capitale, qui renverse le tout. Je seray bien aise d'avoir vostre approbation, et n'en scaurois douter puis que j'ay celle de Mr. le M. de l'Hospital²⁶⁾. J'adjoute dans ce mesme paquet, puisque vous le souhaitez²⁷⁾, l'extrait du livre de Wallis que l'on m'avoit envoiè d'Angleterre²⁸⁾, devant que j'eusse receu le livre mesme.

Vos considerations sur l'avancement de la medecine²⁹⁾ sont fort bonnes et ce que vous projettez ne paroit pas tout à fait impraticable.

En entreprenant le Traitè de vostre nouveau Calcul³⁰⁾, je vous recommande de le rendre autant clair qu'il est possible et qu'il puisse se rapporter principalement à ce qui pourroit avoir usage dans la geometrie, où je doute si ces equations exponentiellement transcendantes³¹⁾ pourront avoir lieu. J'y contribueray volontiers l'exemple du probleme de Mr. Bernoulli le medecin, quoyque ce que j'en ay dans mes brouillons³²⁾, que je viens de revoir, soit si abregè et denuè d'eclaircissement, que j'auray de la peine à y rentrer.

Je crois vous avoir communiquè³³⁾ cy-devant la solution que pretendoit donner Mr. Fatio à ce que j'objectois contre sa theorie de la pesanteur, et que je n'en estois nullement satisfait. C'est pourquoy je m'etonne qu'il vous ait mandè le contraire³⁴⁾. Je ne vois pas qu'on ait encore apportè de difficultè considerable contre la cause que j'ay expliquée dans mon discours, et l'on me fera plaisir de me les proposer, lors qu'on en rencontrera. Pour ce qui est du mouvement absolu et relatif, j'ay admirè vostre memoire, de ce que vous vous estes souvenu, qu'autrefois j'estois du sentiment de Mr. Newton, en ce qui regarde le mouvement circulaire. Ce qui est vray, et il n'y a que 2 ou 3 ans que j'ay trouvè celuy qui est plus

24) Voir la pièce N^o. 2869.

25) Voir la note 17 de la Lettre N^o. 2813.

26) Voir la Lettre N^o. 2838, à la page 564.

27) Consultez la Lettre N^o. 2863, à la page 646 et N^o. 2866, à la page 651.

28) Par D. Gregory; voir la Lettre N^o. 2859, à la page 622.

29) Voir la Lettre N^o. 2863, à la page 639.

30) La minute a: ‘vostre calcul differentiel’. Voir, sur ce ‘Traité’ projeté, la Lettre N^o. 2863, à la page 640.

31) Consultez toujours la Lettre N^o. 2863, à la page 640.

32) Voir la pièce N^o. 2821, où ces brouillons ont été reproduits pour la plus grande partie.

33) Voir la Lettre N^o. 2854, à la page 613.

34) Voir la Lettre N^o. 2863, à la page 644.

[p. 670]

veritable³⁵⁾, duquel il semble qu vous n'estes pas eloignè non plus maintenant, si non en ce que vous voulez, que lorsque plusieurs corps ont entre eux du mouvement relatif, ils aient chacun un certain degrè de mouvement veritable, ou de force, en quoy je ne suis point de vostre avis.

Je vois qu'on a mis bien amplement pour la seconde fois dans les Acta la solution de Mr. le M. de l'Hospital³⁶⁾, du probleme de Bernoulli, qui estant assez embarassée, il me semble que la miene merite pour le moins autant d'y paroitre. C'est pourquoy je vous l'envoie icy³⁷⁾, et vous prie de la faire tenir à ces Messieurs a Leipsich.

Ils pourront corriger à cette occasion, s'ils ne l'ont pas desia fait, les 2 fautes que je vous marquay dans ma precedente³⁸⁾. En leur envoiant vos considerations³⁹⁾ sur le discours de Mr. Bernoulli, vous me ferez plaisir de faire aussi mention des mienes⁴⁰⁾, autant que vous les trouverez bien fondees. Je suis parfaitement etc.

Apres avoir copié la construction du probleme, je me repens presque d'en avoir pris la peine. Je le laisse à vostre jugement si vous croiez, qu'il vaut la peine qu'elle paraisse dans les Acta⁴¹⁾.

35) Voir la note 47 de la Lettre N^o. 2854. Nous regrettons de ne pas connaître les considérations qui ont déterminé l'opinion de Huygens, d'autant plus que nous croyons qu'elles auront été d'autre nature que celles de Leibniz, mentionnées dans la note 25 de la Lettre N^o. 2863.

36) Voir le commencement de la Lettre N^o. 2866 et surtout la note 4 de cette lettre.

37) Voir l'Appendice N^o. 2875 à la présente lettre.

38) Voir la Lettre N^o. 2856.

39) Celles de la Lettre N^o. 2871. On les retrouve en grande partie dans l'article de Leibniz des ‘Acta’ d'août 1694, cité dans la note 22 de la Lettre N^o. 2841.

40) Leibniz y donna suite en faisant insérer dans les ‘Acta’ de septembre 1694 la traduction latine d'une grande partie de la présente lettre. Voir notre pièce N^o. 2874.

41) La phrase ‘si vous croiez, qu'il vaut la peine qu'elle paroisse dans les Acta’ manque dans la minute.