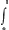ment de la longitude du corps, puisqu'elles dependent plus tost des changemens du contenu solide; ainsi la figure d'une lame elastique ne me paroissant pas assez arrestée, j'avois esté d'autant moins porté à l'examiner. Les theoremes sur les cercles osculateurs (dont les centres sont dans vos courbes generatrices par evolution) que M. le professeur Bernoulli considere comme des clefsGa naar voetnoot7), ne me paroissent point difficiles à trouuer et sans aucune inspection de la figure, par le seul calcul des differences on en trouve, et des plus generaux; non seulement pour la grandeur du rayon de ce cercle, mais encor pour la position du centre car lors qu'on veut chercher la generatrice evolutive d'une ligne qui n'est donnée que differentiellement, le calcul meme ordonne qu'on passe aux differentio-differentielles, et quand on n'auroit pas ces theoremes on les employe virtuellement et sans y penser. je remarque un peu d'emulation entre les deux freres, mais elle est louable et leur sert d'eguillon. Je n'entreray point dans l'examen des Elastiques et de leur proprietés. Car je n'ose gueres m'enfoncer dans des nouueaux travaux qui demandent trop d'attachement, surtout quand la chose a esté faite; car de pouuoir dire et nos hoc poteramus, ce n'est pas une raison suffisante pour moy qui dois menager mon temps. Je n'ay pu
m'empescher de sourire un peu, quand il dit que pour me faire honneur, il veut appeller les courbes ou grandeurs ordinaires, AlgebraiquesGa naar voetnoot8). Car je ne voy pas quel honneur m'en revienne. Je voudrois plus tost qu'il n'appellât pas les autres Mecaniques.
| |
Il dit p. 271, que la maniere de resoudre la Catenaire par des points (qui ne demandent qu'une seule grandeur constante transcendente, la quelle donnée, on n'a plus besoin des quadratures) est veritablement la plus parfaite qu'on puisse employer pour les transcendentesGa naar voetnoot9), mais, que le mal est qu'elle n'est pas universelle, et n'a lieu qu'a l'egard de celles qui dependent de la quadrature de l'Hyperbole, et ne pouuant estre employée à son avis pour ce qui depend de la quadrature du cercle, ny pour des quadratures plus composées. Mais je ne suis pas en cela de son sentiment, car la meme maniere reussit aussi pour la quadrature du cercle; se servant de la section des angles, comme pour l'hyperbole on se sert de la section des raisons. Et il y a une infinité d'autres constructions semblables qui pourront servir pour d'autres lignes transcendentes.
Il donne aussi p. 271. 272. un indice qui doit servir pour connoistre si une quadrature se peut reduire a celle de l'Hyperbole, mais cet indice n'est point universel, et on peut donner une infinité d'instances, ou la reduction reussit, sans que cet indice ait lieuGa naar voetnoot10).
Il prend les series de pag. 274 pour nouuelles, mais Mons. Newton et moy, nous les avons employées il y a long tempsGa naar voetnoot11).
Enfin je viens à la construction que M. Bernoulli donne de mon probleme de la ligne isochrone paracentrique, comme je l'appelle, ou le mobile pesant s'approche ou s'eloigne egalement d'un même point. Cela m'oblige de reprendre mes vieilles meditations la dessus, que j'auois presque oubliées ou perdues. Il a trouué cette solution par un heureux hazard. Je donneray cependant ma MethodeGa naar voetnoot12) qui
| |
paroistra peut estre plus analytique, et moins dependante d'un secours exterieur. Je l'avois reduite autresfois Ga naar voetnoot13) à la quadrature d'une figure, dont l'abscisse estant x, l'ordonnée est 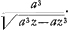 Mais Mons. Bernoulli ayant taché avec raison de construire la courbe demandée non pas tant par une quadrature, que par l'extension ou evolution d'une autre courbe, je l'ay aussi voulu faire à son exemple. La difference qu'il y a entre nous la dessus est qu'il se sert de la rectification d'une courbe qui est elle même deja transcendente, scauoir de son Elastique, et qu'ainsi sa construction est transcendente du second genre, au lieu que me je sers seulement de la rectification d'une courbe ordinaire dont je donne la construction par la Geometrie commune. Au reste je me rapporte à mes precedentes, sur les quelles je vous supplie de repasser et de me donner les lumieres que j'y souhaitte à l'egard de plusieurs points qui ont esté touchés entre nous. En vous souhaittant une parfaite santé je suis avec zele
Monsieur
Vostre treshumble et tres obeissant serviteur Leibniz.
Hanover ce 7/27 Juillet 1694. |
-
voetnoot1)
- Chr. Hugenii etc. Exercitationes Mathematicae, Fasc. I, p. 192.
-
voetnoot2)
- Leibnizens Mathematische Schriften, Band II, p. 187, et Briefwechsel, p. 741.
-
voetnoot3)
- Le fragment contenait sans doute les deux articles de Jacques Bernoulli qui se suivent dans ce numéro et dont nous avons cité le second dans la note 22 de la Lettre No. 2841, tandis que le premier porte le titre: ‘Jac. B. Curvatura laminae elasticae. Ejus Identitas cum Curvatura Lintei a pondere inclusi fluidi expansi. Radii Circulorum Osculantium in terminis simplicissimis exhibiti, una cum novis quibusdam Theorematis huc pertinentibus, &c.’
-
voetnoot4)
- Allusion au début du second article de Jacques Bernoulli, où on lit: ‘Felicitatem inventi praecedentis’ [c'est-à-dire de la construction de la courbe élastique dont la rectification va servir à la solution du problème dont il va traiter] ‘commendare potest solutio elegantissimi Problematis Leibnitiani, de invenien da Linea, per quam descendens grave aequaliter aequalibus temporibus a dato puncto recedat, vel ad illud accedat: quod laudatissimo suo Auctori ita placuit, ut non tantum ad ejus tentamen Amicos pariter & Adversarios aliquoties in Actis provocarit (vid. Anno 1689, Apr. p. 198, & 1690. Maj. p. 229, & Jul. p. 360) sed & ipse quoque strenue in illo desudarit, testibus nonnullis Curvae proprietatibus, quas Gallorum Diario inseri curavit, ut ex relatione Fratris habes, qui tamen illas
nominare mihi non potuit’. Ajoutons que ce renseignement fourni par Jean Bernoulli était erroné. Leibniz n'avait rien écrit sur la courbe paracentrique en dehors des articles cités que nous avons déjà mentionnés au début de la note 22 de la Lettre No. 2841.
-
voetnoot5)
- Voir dans les ‘Acta’ d'août 1694, l'article de Leibniz sur la courbe isochrone paracentrique, que nous avons cité dans la note 22 de la Lettre No. 2841 et qui commence par la phrase: ‘A celeberrimo Viro Jac. Bernoullio, Matheseos apud Basileensis Professore, in Actis mensis Junii nuperi velut invitatus; praesertim circa problema a me olim, cum nondum nostra calculandi methodus frequentari coepisset, propositum; responsionem defugere nolui; tametsi & valetudo vacillans & aliae multiplices causae, excusare me fortasse possent’.
-
voetnoot6)
- Leibniz ici fait allusion au passage suivant, qu'on trouve dans le premier des deux articles de Jacques Bernoulli mentionnés dans la note 3: ‘Vulgaris (ut modo dixi) est hypothesis, extensiones viribus tendentibus proportionales esse: qua & usus olim Celeberrimus Dn. Leibnitius in acutissima sua lucubratione de Resistentia solidorum; & ipsemet ego in praesente materia, prius quam generalem Problematis constructionem adinvenissem. Quapropter operae praetium existimo, naturam & proprietates Curvae nostrae in hac hypothesi paulo specialius exponere: quanquam pro ipsa hypotheseos hujus, sicut & pro cujusvis alterius, veritate multum militare nolim,
persuasum potius habens, nullam constantem tensionum legem in natura observari, sed eam pro diversa corporum textura diversam existere; id quod experimenta tum nostra tum aliorum abunde confirmare videntur, quorum plurima praelaudatur Author industrius’ [Franciscus Tertius de Lanis] ‘Magisterii naturae & artis, loco cit.’ [Tom. 2. lib. 7] ‘recenset’.
L'article mentionné de Leibniz était celui qui parut dans les ‘Acta’ de juillet 1684 sous le titre: ‘Demonstrationes novae de resistentia Solidorum, autore G.G.L.’
-
voetnoot7)
- Il s'agit de diverses expressions analytiques très élégantes pour le rayon de courbure en coordonnées cartésiennes et polaires au moyen des différentielles du second ordre. On les rencontre aux pages 264 et 265 de l'article cité.
-
voetnoot8)
- A la page 269 de l'article cité, où Bernoulli, après avoir mentionné le cas qu'une courbe serait ‘ex numero Geometrarum’, ajoute encore: ‘h.e. Algebraicarum (sic enim illas posthac appellabo in honorem Viri celeberrimi, qui hoc nomine dessignatas cupit’. Comme on le sait, l'expression ‘courbe algébrique’ s'est maintenue avec le sens précis, que l'on y trouve attaché par Jacques Bernoulli.
-
voetnoot9)
- En consultant la page citée on voit qu'il s'agit de la méthode de Leibniz ‘construendi Catenariam ope solius Logarithmicae absque suppositione quadraturae’. Comparez la Lettre No. 2688 aux pages 110 et 111.
-
voetnoot10)
- En effet, cet indice dont Jacques Bernoulli voudrait qu'on se serve pour découvrir si une courbe ‘mécanique’, donnée par son équation différentielle, peut être construite, ou non, au moyen des logarithmes, n'était applicable qu'au cas où cette équation se laissait réduire à la forme dy=f(x)dx, et même alors il ne consistait, exprimé en langage moderne, que dans la recherche d'une fonction algébrique φ (x), choisie de telle manière qu'on aurait φ' (x)∷φ(x)=f(x); et pour trouver cette fonction Bernoulli n'indique d'autre moyen que celui de chercher une courbe y=φ(x) dont la soustangente serait égale à f(x)-1.
-
voetnoot11)
- Les séries en question ne représentent en effet que le développement, au moyen de la formule du binôme, des intégrales
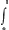 x2(1-x4)-½dx et x2(1-x4)-½dx et 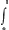 (1-x4)-½dx, méthode connue depuis longtemps par Leibniz et par Newton, qui la publia par l'intermédiaire de Wallis dans les Chapitres 85 et 91 de l'ouvrage de 1685 cité dans la note 3 de la Lettre No. 2660. Consultez encore la note 6 de la Lettre No. 2723. (1-x4)-½dx, méthode connue depuis longtemps par Leibniz et par Newton, qui la publia par l'intermédiaire de Wallis dans les Chapitres 85 et 91 de l'ouvrage de 1685 cité dans la note 3 de la Lettre No. 2660. Consultez encore la note 6 de la Lettre No. 2723.
|
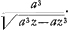 Mais Mons. Bernoulli ayant taché avec raison de construire la courbe demandée non pas tant par une quadrature, que par l'extension ou evolution d'une autre courbe, je l'ay aussi voulu faire à son exemple. La difference qu'il y a entre nous la dessus est qu'il se sert de la rectification d'une courbe qui est elle même deja transcendente, scauoir de son Elastique, et qu'ainsi sa construction est transcendente du second genre, au lieu que me je sers seulement de la rectification d'une courbe ordinaire dont je donne la construction par la Geometrie commune. Au reste je me rapporte à mes precedentes, sur les quelles je vous supplie de repasser et de me donner les lumieres que j'y souhaitte à l'egard de plusieurs points qui ont esté touchés entre nous. En vous souhaittant une parfaite santé je suis avec zele
Mais Mons. Bernoulli ayant taché avec raison de construire la courbe demandée non pas tant par une quadrature, que par l'extension ou evolution d'une autre courbe, je l'ay aussi voulu faire à son exemple. La difference qu'il y a entre nous la dessus est qu'il se sert de la rectification d'une courbe qui est elle même deja transcendente, scauoir de son Elastique, et qu'ainsi sa construction est transcendente du second genre, au lieu que me je sers seulement de la rectification d'une courbe ordinaire dont je donne la construction par la Geometrie commune. Au reste je me rapporte à mes precedentes, sur les quelles je vous supplie de repasser et de me donner les lumieres que j'y souhaitte à l'egard de plusieurs points qui ont esté touchés entre nous. En vous souhaittant une parfaite santé je suis avec zele