Oeuvres complètes. Tome X. Correspondance 1691-1695

N^o 2869.
Christiaan Huygens à H. Basnage de Beauval, rédacteur de l'Histoire des Ouvrages des Scavans.
[juin 1694]¹⁾.
Appendice au No. 2868.

Une partie de la minute²⁾ et la copie se trouvent à Leiden, coll. Huygens.
La pièce a été publiée dans l'Histoire des Ouvrages des Sçavans pour les mois de Mars, Avril & Mai 1694, sous le mois d'Avril, p. 355.
Une traduction latine a paru dans les Opera Varia, p. 305.
La pièce est la réponse au No. 2848.
Renau y répondit par le No. 2881.

Replique de Mr. Huguens à la Reponse de Mr. Renau, Ingenieur General de la Marine en France.

Ce que j'avois avancé dans ma Remarque, inserée dans la Bibliotheque Universelle du mois de Sept. 1693.³⁾ touchant l'erreur capitale qui est dans le Traité de la Manoeuvre des Vaisseaux de M. Renau, me sembloit assez clair; & des per-

1) Quoique la pièce parût dans l'Histoire des Ouvrages des Sçavans, sous le mois d'avril 1694, il est certain qu'elle n'était pas encore achevée le 29 mai 1694, puisque sous cette date Huygens demanda l'opinion de Leibniz sur le sujet de sa polémique avec Renau ‘pour l'alleguer dans la replique que je vay y faire’ c'est-à-dire à la ‘Réponse’ de Renau (voir la Lettre N^o. 2854 à la page 611). La pièce a donc été antidatée par le Rédacteur de l'‘Histoire’.

2) Elle occupe la page 107 du Livre J. Elle a quelques variantes de peu d'importance, dont nous indiquerons toutefois quelques-unes dans les notes.

3) Voir la pièce N^o. 2826.

[p. 655]

sonnes tres-versées⁴⁾ dans les Mathematiques, avoient jugé qu'il étoit sans replique. C'est pourquoy je n'avois pas cru qu'il y voudroit faire reponse pour soutenir sa Theorie. Cependant il paroît par ce qu'il a publié⁵⁾. qu'il ne s'est pa tenu pour convaincu. Et comme il se sert de raisonnemens qui pourroient donner quelque peine à demêler à ceux qui n'ont pas assez penetré ces matieres, je me trouve obligé de montrer encore avec plus d'evidence que je n'ai fait, que sa Theorie ne peut être soutenuë qu'en renversant les principes de la Mechanique établis dès long tems, & dont il n'oseroit ni ne voudroit nier la verité.

Pour ne pas allonger inutilement nôtre dispute, en m'arrêtant à plusieurs raisons que Mr. Renau m'oppose, je montrerai seulement que comme j'avois remarqué, il s'est mepris dans la proposition sur laquelle roule toute sa Theorie; après quoi j'indiqueray en peu de mots ce qui a pu donner occasion à son erreur.

Pour faire voir de quoi il est question, je repete ici les mêmes choses pour la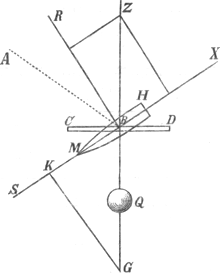



plûpart qui etoient supposées dans nos figures⁶⁾, savoir que HM est la quille d'un vaisseau, sa vergue ou voile CD, AB la ligne du vent qui pousse la voile. BG est perpendiculaire sur CD, GK perpendiculaire sur BK, qui est la quille prolongée. Je prolonge aussi GB en Z, & MH en X.

Mr. Renau dit dans sa Theorie, chap. II art. 1.⁷⁾ que si on suppose que le vaisseau fend l'eau de tous côtez avec la même facilité qu'avec sa pointe, il sera poussé par le vent en sorte qu'il avancera selon la droite BG, ce qui est vrai. Mais si la position de sa quille ne lui permet que d'avancer dans la droite BK; ou bien si une corde BR, perpendiculaire sur BK, & dont la longueur est censée infinie, l'oblige de tenir cette route de BK; il soutient que la voile & le vent demeurant comme auparavant, le vaisseau parcourra l'espace BK, dans le même tems qu'il auroit parcouru BG; & moi je dis qu'il parcourra l'espace BS, moyen proportionel entre BK & BG. Voilà le grand point⁸⁾ de nôtre dispute.

4) De l'Hospital était du nombre (voir la Lettre N^o. 2838 au bas de la page 564), de la Hire aussi (voir la Lettre N^o. 2859 à la page 624). La réponse de Leibniz à la question mentionnée dans la note 1 de la présente pièce était moins décisive; voir la Lettre N^o. 2863, à la page 642.

5) La pièce N^o. 2848.

6) Voir la figure de la page 526 et consultez, sur la figure de Renau, la note 4 de la pièce N^o. 2848.

7) Voir, sur le contenu de cet article, les pages 525 et 526 de la pièce N^o. 2826.

8) La minute a ‘le point essentiel’.

[p. 656]

Dans la preuve qu'il apporte dans sa Reponse⁹⁾, au lieu du vent AB, qui tombe obliquement sur la voile CD, il substitue¹⁰⁾ le vent ZB, qui la frappe perpendiculairement; ce qui est permis, & il n'en arrive aucun changement à nôtre question; étant certain que de quelque sens que le vent tombe sur cette voile CD, il fait effort pour faire aller le vaisseau par la route BG, perpendiculaire à CD. Et il ne sert de rien du tout de considerer, comme fait Mr. Renau, les differentes determinations dans le mouvement du vent¹¹⁾. Il trouve en suite par son raisonnement, que la force avec laquelle le vaisseau est poussé par le vent suivant BG par le moyen de la voile, est à la force avec laquelle il est poussé par le même vent, & par le moyen de la même voile, suivant BK, comme le quarré de BG au quarré de BK; et non pas comme BG à BK, ainsi que je pretens; & c'est de quoy tout depend¹²⁾.

Pour savoir qui de nous deux a raison, imaginons nous que le plan où est notre figure soit dressé sur l'horison, en sorte que la ligne BG lui soit perpendiculaire, & que RBX soit une corde attachée en R, à laquelle en B est noué & suspendu le poids Q. Concevons de plus que la partie BX, perpendiculaire à RB, soit retenuë par la main en X. Il est clair que ceci represente exactement le cas du vaisseau dont il est question. Car au lieu du vent, qui en donnant contre la voile CD, le pousse selon BG, nous avons le poids Q, qui tire le point B selon BG: & la corde, censée infiniment longue, BR, qui faisoit que le vaisseau ne pouvoit avancer que selon BK, fait ici le même effet à l'égard du noeud B.

Donc comme la force avec laquelle le vent pousse le vaisseau selon BG, est à la force dont il le pousse selon BK, ainsi est le poids Q à la pesanteur que sent la main en X, en empêchant le noeud B de se mouvoir selon BK. Car cette pesanteur est égale à la force dont ce noeud est tiré selon BK. Or GK étant parallele a BR, il est certain par les regles très-connues de la Mechanique, que le poids Q est à celui qui retient la corde BX, ou bien à la pesanteur que sent la main en X, comme BG à BK. Donc aussi la force avec laquelle le vent pousse le vaisseau selon BG, est à la force dont il est poussé selon BK, comme BG à BK; & non pas comme les quarrez de ces lignes, comme veut Mr. Renau¹³⁾.

Supposons maintenant que le vaisseau HM, fendant l'eau avec égale facilité de tous cotez, & étant poussé par le vent ZB ou AB, (car il n'importe) aille dans un certain tems par BG, la voile étant en CD; & qu'on veuille savoir combien il

9) Aux pages 591 et 592 de la pièce N^o. 2848.

10) La minute a ‘il emploie’.

11) La minute ajoute la phrase suivante, biffée depuis: ‘Cela ne sert qu'à l'embrouiller et à le faire tomber d'une erreur en l'autre lesquelles je ne prendray pas la peine de detailler, mais je montreray que ce qu'il en conclud est faux’.

12) Ici finit la minute mentionnée dans la note 2.

13) Comparez le second alinéa de la page 591 de la pièce N^o. 2848.

[p. 657]

avancera selon BK, dans un tems égal avec le même vent, & la même position de la voile. Je dis que puis que les vitesses du vaisseau dans ces deux routes, doivent être telles, que les resistances que lui fait l'eau soient comme les forces dont il est poussé, (car ce n'est qu'alors qu'il avance avec un mouvement égal) & que ces resistances sont comme les quarrez des vitesses; il faut donc que les quarrez des vitesses soient comme les forces, c'est à dire comme GB à BK. Et par conséquent que les vitesses soient comme GB à BS; puis que les quarrez de GB, BS, sont comme les lignes GB à BK par la construction. J'ai donc prouvé par les principes ordinaires de la Mechanique, que ce que j'avois avancé dans ma Remarque est veritable.

Il seroit superflu d'examiner les autres argumens de Mr. Renau, par leiquels il veut confirmer cette même proposition que je viens de refuter. Je diray seulement que l'origine de l'erreur qui se trouve dans tout cela, vient principalement de ce que dans l'art. 7 du I. chap.¹⁴⁾ de sa Theorie, il conclut que les forces relatives d'une matiere fluide à des superficies diversement inclinées, sont entre elles comme les quarrez des sinus de leurs angles d'incidence, sans se souvenir qu'il devoit dire, à des superficies égales diversement inclinées: lequel mots d'égales il a encore oublié un peu devant dans le même article pag. 7. Si on le supplée, alors la demonstration, & ce qu'elle conclut sont comme il faut, & dans les mêmes principes du P. Pardies dans l'art. 118 de ses Forces mouvantes¹⁵⁾, qui sont veritables. Seulement ce Pere s'est trompé dans ce même article, parce qu'il n'a pas su, ou qu'il ne s'est pas souvenu, que les resistances de l'eau contre un corps sont comme les quarrez des vitesses de ce corps; car c'est pour cela que pag. 225. il fait af à au en raison doublée de bo à mp, au lieu qu'il devoit faire simplement af à au comme bo à mp.

Pour ce qui est de la plus avantageuse position du Gouvernail, je dis que Mr. Renau se condamne à tort soi-même, & que voulant corriger sa premiere recherche, il raisonne mal pag. 24. de sa Reponse¹⁶⁾; parce qu'il s'agit uniquement de savoir dans quelle situation du Gouvernail l'eau le poussera avec le plus de force, selon la perpendiculaire à la quille; car de la s'ensuivra necessairement le

14) Voici l'article en question: ‘S'il y avoit donc un mesme nombre de petits corps d'une matiere fluide, qui frapassent des superficies diversement inclinées; les forces relatives de cette matière, à ces superficies, seroient entr'elles, dans la mesme proportion que celles d'un seul corps, c'est à dire, comme les sinus de leurs Angles d'incidence. Mais il y a un plus grand nombre de ces corps qui frappent les superficies qui sont moins inclinées, que les superficies que le sont plus, & cela encore dans la proportion des sinus des Angles d'incidence; Donc ces forces relatives seront entr'elles, en raison doublée des sinus de leurs Angles d'incidence, ou, ce qui est la mesme chose, comme les quarrez de ces sinus sont entr'eux’. Après quoi Renau fait suivre la ‘Demonstration’ qui conclut par la phrase, citée par Huygens.

15) Consultez, sur cet article 118, la note 10 de la pièce N^o. 2848.

16) Voir les pages 594 et 595 de la pièce N^o. 2848.

[p. 658]

plus de vitesse du derriere du vaisseau dans cette perpendiculaire. Il verra aussi qu'il se trompe quand il veut que pag. 25. de sa Theorie de la Manoeuvre des vaisseaux, on lise vitesse au lieu de force¹⁷⁾.

Je remarque au reste que toute cette Theorie, comme il l'avoit donnée, seroit vraye, si les resistances de l'eau etoient comme les vitesses du vaisseau, au lieu qu'elles sont comme les quarrez de ces vitesses.

17) Comparez la page 594 de la pièce N^o. 2848.