Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 588]

N^o 2848.
B. Renau à Christiaan Huygens.
Appendice au No. 2847.
[janvier 1694].

La pièce a été reproduite dans les livraisons du 16 et du 23 mai 1695 du Journal des Sçavants pp. 329-337 et 355-363 de l'édition d'Amsterdam¹⁾.
's Gravesande en donna une traduction latine dans les Chr. Hugenii Opera Varia, p. 296.
Elle est la réponse à la pièce No. 2826.
Chr. Huygens y répondit par le No. 2869.

Réponse de M. Renau à M. Huguens²⁾.

Mr. Huguens dit³⁾: Que bien qu'on puisse imaginer que le mouvement au vaisseau par BG est composé des mouvemens par BK & KG, il ne s'ensuit pas que si dans l'efet on lui laisse le seul mouvement suivant BK....que le vent qui en poussant la voile CD, le pousseroit de B en G, le pousser a dans un temps égal de B en K. Et c'est en cela où je trouve d'abord qu'il se trompe. Car afin que le

1) Elle y est précédée d'une Introduction intitulée: ‘Remarque de M. Huguens sur le Livre de la Manoeuvre des vaisseaux imprimée à Paris in-8.’ (p. 310) et ainsi conçue: ‘Mr. Renau Capitaine de Vaisseau, & depuis Ingenieur General de la Marine & Chevalier de l'Ordre de Saint Louis, donna au Public en 1689. un traité de la Manoeuvre des Vaisseaux, qui fut merveilleusement bien reçu. M. Huguens qui est le seul qui y a trouvé à redire avouë luy mesme que cet ouvrage est écrit avec beaucoup de soin & de neteté, & qu'on n'y supose point de principes qui ne soient veritables; en sorte que si toute la theorie estoit tirée de là par des consequences legitimes, il n'y auroit rien à reprendre: mais comme il ne lui paroit pas que cela soit ainsi, il a cru qu'il seroit bon pour l'utilité du public d'avertir d'une erreur considerable qu'il croit avoir reconnuë dans ce traité. M. Renau soutient au contraire qu'il n'est pas tombé dans cet erreur, & que s'il s'est trompé en quelque endroit de cet ouvrage, c'est touchant un point que M. Huguens croit tres conforme à la raison’.
‘Les preuves des deux parties ayant trop d'étenduë pour trouver place dans un seul Journal, on a cru qu'il seroit à propos de mettre dans celui-ci l'objection de M. Huguens & de reserver la réponse de M. Renau pour le suivant’.
‘Voici l'objection de M. Huguens comme elle se trouve inserée dans la Bibliothèque Universelle et Historique du mois de septembre 1693’.
Après ce début, l'article fait suivre la ‘Remarque de Huguens sur le Livre de la Manoeuvre des Vaisseaux’, elle-même, notre pièce N^o. 2826, à commencer par la phrase: ‘Je commencerai en raportant le contenu de l'Article I du 2. Chapitre’, etc. (p. 525) jusqu'à la fin.
Consultez d'ailleurs sur la pièce présente la note 2 de la Lettre N^o. 2847.

2) Il est probable que l'écrit primitif contenait une introduction, qui nous manque, puisqu'elle a été remplacée dans la reproduction de 1695 par celle citée dans la note précédente.

3) Consultez la page 527 de la pièce N^o. 2826.

[p. 589]

vaisseau puisse aller de B en G dans un mesme temps déterminé, (voyez la figure du Journal précedent)⁴⁾ il faut qu'il ait réellement dans la détermination BK une vitesse capable de faire dans un temps égal la quantité BK, & dans la détermination KG la quantité KG. Et afin qu'on ne puisse pas douter de cete verité, imaginons-nous que le vaisseau est poussé dans la détermination BK d'une force capable de le faire aller dans un certain temps déterminé de B en K; & qu'en mesme temps il soit aussi poussé dans le sens KG d'une force capable de lui faire faire dans le mesme temps déterminé la quantité KG: comme ces deux forces n'ont rien d'oposé l'une à l'autre, ni qu'elles ne concourent point ensemble, atendu que BK est perpendiculaire à KG, le vaisseau obeïra entiérement à chacune de ces deux forces, & par consequent la vitesse qu'il aura dans chaque instant dans le sens BK, sera à [la] vitesse qu'il aura dans les mesmes instans dans le sens KG comme BK est à KG. C'est pourquoi le vaisseau satisfaisant à l'efet de ces deux forces, se mouvra le long de BG, & parviendra en G dans le temps déterminé. Et par consequent si dans l'efet on lui laisse le seul mouvement par BK, la force telle qu'elle puisse estre qui le pousseroit de B en G, le poussera dans un temps égal de B en K, puis qu'en rendant inutile l'efet de la partie de la force qui convient pour parcourir en mesme temps KG, on n'augmente ni on ne diminuë, comme nous avons dit, la vitesse selon BK. J'avouë que si l'angle BKG estoit aigu, la force particuliere qui pousseroit le vaiseau selon KG, diminueroit la vitesse qu'il auroit selon BK, comme lui estant oposée: au contraire, si l'angle BKG estoit obtus, elle augmenteroit comme allant du mesme sens; mais comme l'angle BKG est droit, cete force ne diminuë ni n'augmente la vitesse du vaisseau selon BK.

M. Huguens dit aprés: Car pour sçavoir quel espace il parcourr a par BK, il faut voir avec quelle sorce il est poussé dans cete route, & de plus avoir égar d à la resiflance qu'il soufre de l'eau. Je viens de faire voir que les raports des vitesses dans les diferentes déterminations perpendiculaires l'une à l'autre, sufisoient pour faire voir la route du vaisseau, sans avoir besoin du raport des forces, ni des resistances de l'eau; mais comme ces vitesses dépendent des forces, je puis faire voir la mesme chose par le raport des forces.

J'ai démontré au 13. art. du 1. chap. de la Theorie de la Manoeuvre des Vaisseaux, dont M. Huguens convient, que les forces qui poussoient le vaisseau estoient entr'elles comme les quarrez des vitesses. C'est pourquoi la force qui convient pour faire faire au vaisseau la quantité BK dans le sens BK, dans un temps déterminé, est à la force qui convient pour faire faire au vaisseau la quantité KG

4) Elle est identique dans tous les points essentiels avec celle de la pièce N^o. 2826, p. 526, à laquelle nous renvoyons; seulement on doit ajouter à cette sigure une perpendiculaire AV, abaissée du point A sur la droite DCO.

[p. 590]

dans le sens KG, comme le quarré BK est au quarré de KG: d'où il suit que si le vaisseau estoit poussé en mesme temps dans les deux déterminations que je viens de dire, qui sont perpendiculaires l'une à l'autre, il auroit une force égale à ces deux forces, atendu que l'une n'ajoute ny ne diminuë rien à l'autre. Ainsi cete force seroit exprimée par le quarré de BG, parce que le quarré de BG est égal au quarré de BK & de KG. De maniere que le vaisseau aura alors une vitesse qui sera produite par cete force, c'est à dire que le vaisseau fera la quantité de BG dans le mesme temps qu'il a esté dit. C'est pourquoi si le vaisseau estoit poussé selon BG avec la force exprimée par le quarré de BG, il ariveroit en G en mesme temps qu'il ariveroit en K, s'il estoit poussé selon BK avec une force exprimée par le quarré de BK.

M. Huguens continuë de cete sorte: Or il est certain par les regles de Mecanique, que la force avec laquelle la voile DC pousse le vaisseau par BK, est à celle dont la mesine voile, & dans la mesme position a l'égard du vent, la pousseroit par BG comme BK à BG. Je ne conviens point que cela soit selon les regles de Mecanique, au contraire il est certain que le raport de ces forces est comme le quarré de BK au quarré de BG, & non pas comme BK à BG; & pour qu'on n'en puisse pas douter, imaginons-nous presentement que l'air se meuve suivant la ligne AB une fois plus vîte dans un temps que dans un autre. Lors qu'il se mouvera une fois plus vîte, il frapera la voile quatre fois plus fort, atendu que chaque partie frape une fois plus fort à cause d'une fois plus de vitesse, & à cause d'une fois plus de vitesse il y a aussi une fois autant de parties qui frapent en mesme temps. C'est pourquoi la vitesse estant double & la masse double, la puissance ou la force est quadruple. Si la vitesse estoit triple, chaque partie fraperoit trois fois aussi fort, parce que la vitesse est triple; & aussi parce que la vitesse est triple il y auroit trois fois autant de parties qui fraperoient en mesme temps. C'est pourquoi la vitesse estant triple & la masse triple, la puissance ou la force sera neuf fois aussi grande; d'où on voit que la masse augmente en mesme raison de la vitesse, & chaque partie srapant aussi plus fort à raison de la vitesse, la puissance ou la force du vent contre la voile, est en raison doublée des vitesses du vent; c'est à dire en raison des quarrez des vitesses du vent contre la voile. M. Huguens convient de ce principe: ainsi il ne s'agit plus qu'à en faire l'aplication.

La premiere aplication sera pour faire voir pourquoi la force du vent contre la voile, lors que le vent est perpendiculaire à la voile, est à la force du mesme vent contre la voile lors qu'elle est inclinée au vent, comme le quarré du rayon est au quarré du sinus de l'angle d'incidence, ou, ce qui est la mesme chose, pourquoi les forces d'un mesme vent contre des voiles diversement inclinées au vent, sont entr'elles en raison des quarrez des sinus des angles d'incidence; ce que j'ai démontré dans les articles 7. 8. & 9. du chap. 1. & que je prouve encore de cete maniere. J'ai fait voir dans la Theorie de la Manoeuvre des vaisseaux au 6. art. du chap. 1. qu'un corps qui se mouvoit de A en B, ne rencontroit la superficie

[p. 591]

CD qu'avec sa détermination AT⁵⁾, suposant AT⁵⁾ perpendiculaire sur DC prolongée, & ne faisoit d'impression sur cete superfsicie que suivant cete détermination, & M. Huguens en convient. Cela estant, le vent AB n'agit contre cete voile que suivant cete détermination, c'est à dire avec la vitesse AT⁵⁾. Et si la voile CD estoit perpendiculaire au vent AB, ce vent agiroit contre la voile avec la vitesse AB. Et par consequent par le principe que je viens d'établir ci-devant, la force avec laquelle le vent agiroit contre cete voile si elle estoit perpendiculaire au vent, est à la force du vent contre la voile CD qui est inclinée au vent, comme le quarré de AB est au quarré de AT⁵⁾, c'est à dire comme le quarré du rayon est au quarré du sinus de l'angle d'incidence.

La seconde aplication est celle qui sert à résoudre la question dont M. Huguens & moi ne sommes pas d'acord, c'est à dire pour faire voir que lors que la voile est dans la situation CD, & le vaisseau dans celle de BK, la force avec laquelle le vaisseau est poussé par le vent suivant BG, par le moyen de la voile, est à la force avec laquelle il est poussé par le mesme vent, & par le moyen de la mesme voile suivant BK, comme le quarré de BG est au quarré de BK, & non pas comme BG est à BK, comme M. Huguens le prétend.

Pour le faire voir, imaginons-nous que le vent frape la voile avec la vitesse BG. Comme il ne la frape qu'avec un mouvement suivant BG, il faut regarder le vent comme allant de B en G avec la vitesse de BG. Mais lors qu'il va de B en G avec cete vitesse, il va dans la détermination de BK avec la vitesse de BK, & dans le sens de KG avec la vitesse de KG. C'est pourquoi par ce que j'ai dit ci devant, la force avec laquelle le vaisseau est poussé suivant BG, est à celle avec laquelle il est poussé suivant BK, comme le quarré de BG est au quarré de BK: & à celle avec laquelle il est poussé suivant KG, comme le quarré de BG est au quarré de KG; & on remarquera que la mesme force du vent contre la voile, c'est à dire la force totale suivant BG, qui est exprimée par le quarré de BG, est divisée suivant BK & suivant KG en deux parties, dont la somme est égale à la totale, & en cela la force, la puissance ou le mouvement, qui sont trois mots pour signifier la mesme chose, ne reçoit ni augmentation ni diminution par nos manieres d'envisager le mouvement, qui ne consiste pas dans la vitesse seule des corps, il y faut encore comprendre les masses. Ainsi la puissance, la force ou le mouvement, est le produit de la vitesse par le masse. C'est pourquoi une mesme puissance qui a esté produite par deux puissances, est égale à ces deux puissances, pourvu que la détermination de l'une soit perpendiculaire à la détermination de l'autre, parce qu'en ce cas là ces deux puissances ne peuvent rien ajouter l'une à l'autre, ni rien ôter l'une de l'autre, les deux déterminations n'ayant rien l'une contre l'autre ni

5) Lisez ‘AV’ et consultez la note précédente.

5) Lisez ‘AV’ et consultez la note précédente.

5) Lisez ‘AV’ et consultez la note précédente.

5) Lisez ‘AV’ et consultez la note précédente.

[p. 592]

l'une pour l'autre, comme nous avons dit. C'est ce qui fait qu'une puissance suivant BK peut demeurer la mesme, & par consequent son efet toujours le mesme, quoi qu'on augmente ou diminuë à l'infini la puissance suivant KG. En ce cas-là il n'ariveroit de changement qu'à la puissance totale BG qui sera toujours égale à la somme des deux puissances qui l'auront produite.

Il s'ensuit de tout ce que je viens de dire, que le vaisseau HBM estant poussé selon BG par le moyen de la voile DC, la vitesse avec laquelle le vaisseau se meut de côté, estant à celle avec laquelle il se meut de pointe, comme GK à LK⁶⁾; il s'ensuit, dis-je que le vaisseau ira le long de BL, & arivera en L dans le mesme temps qu'il seroit arivé en G, s'il fendoit l'eau de tous côtez avec la mesme facilité qu'il la fend de pointe, & si le vaisseau estoit ataché, comme dit M. Huguens, avec une corde BR infiniment longue & perpendiculaire à BK: c'est à dire pour empêcher que le vaisseau ne se must aucunement selon la détermination KG, il s'ensuivroit que le vaisseau ariveroit encore au point K, au mesme temps qu'il seroit arivé au point G, ce qui estoit en question, & ce qu'il faloit prouver.

Si la regle de Mecanique dont parle M. Huguens, sçavoir que la force avec laquelle DC pousse le vaisseau selon BK, est à celle avec laquelle la mesme voile pousse le vaisseau selon BG, comme BK est à BG [étoit véritable]; non seulement le vaisseau n'iroit point en K en mesme temps qu'il auroit esté en G dans les circonstances dont on a parlé, mais mesme le vaisseau fendant également l'eau de tous côtez, & la voile DC le poussant selon BG qui lui est perpendiculaire, n'iroit pas selon la ligne BG: Car par la mesme regle de Mecanique la force avec laquelle le vaisseau seroit poussé selon BK par le moyen de la voile, seroit à celle avec laquelle il seroit poussé selon KG, comme BK est à KG, & les vitesses du vaisseau seroient entr'elles comme les racines des forces. Donc les vitesses qui resulteroient de ces forces, sçavoir la vitesse que le vaisseau auroit pris dans chaque instant selon BK, seroit à celle qu'il auroit dans les mesmes instans selon KG, comme la racine de BK est à la racine de KG. Mais pour se mouvoir selon BG, il faut que ces vitesses, lors qu'elles sont inégales, comme nous suposons ici, soient entr'elles dans chaque instant, comme BK est à KG, & non pas comme leurs racines. Donc le vaisseau n'iroit pas selon BG; ce qui est absurde. Car la force totale qui pousse le vaisseau estant selon BG, en suposant que le vaisseau fend l'eau également de tous côtez, il faut qu'il aille necessairement selon cete ligne.

Mr. Huguens dit plus bas⁷⁾: La mesme erreur que je viens de remarquer influe dans presque tout le traité, & empêche de subsister plusieurs theorêmes qui autre-

6) Lisez: comme LK à GK.

7) Voir la page 528 de la pièce N^o. 2826.

[p. 593]

ment paroissent fort élegans, comme entre autres celuy qui dit, que quand l'angle de la voile avec le vent OBA est donné, la plus avantageuse situation de la quille pour gagner au vent est celle qui divise également son complement OBE, dont l'auteur prouve ensuite, &c.

Puis que je viens de faire voir que ce que M. Huguens croyoit une erreur n'en est pas une, tous les theorêmes du traité demeurent entiers.

Ensuite il dit⁸⁾: Au reste M. Renau ne pourra gueres douter que notre regle ne soit vraye puis que par elle on trouve le meilleur angle du gouvernail avec la quille, pour faire tourner le vaisseau le plus promptement, tout à fait tel qu'il l'a déterminé dans le chap. 7. En quoy il a fait une découverte fort utile. Car en prenant⁹⁾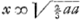



; de mesme qu'il trouve le sinus de l'angle que la quille ou la ligne du mouvement de l'eau fait avec le gouvernail, ce qui doit estre ainsi. Je ne puis estre encore ici du sentiment de M. Huguens ni par consequent de celui de mon livre, où il y a une erreur tres considerable, comme je vas le faire voir. Mais auparavant j'avouerai ingenuement la cause de cete erreur. J'avois premierement fait mon livre en suposant pour vrai un principe faux que le P. Pardies a donné dans la science des forces mouvantes art. 118. quoi que tout son ouvrage sur le mouvement d'un vaisseau¹⁰⁾ ne consiste qu'en ce seul principe, qu'il n'a apliqué à rien, ni donné aucun moyen de resoudre aucune des propositions de la theorie de la manoeuvre des vaisseaux¹¹⁾. Comme je m'apperçus de la fausseté de ce principe à peu près à la fin de l'impression du 1. livre, je le suprimai entiérement, parce que ce principe faux estoit répandu dans toutes les propositions du livre, qui en rendoit toutes les resolutions fausses. Je les resolus toutes de nouveau

8) Voir la page 529 de la pièce N^o. 2826.

9) Intercalez ici: ‘p=a, c'est-à-dire en faisant la ligne du vent perpendiculaire sur la quille, on trouve par cette règle le sinus’.

10) Les articles 115-119 de l'ouvrage de Pardies, cité dans la note 4 de la Lettre N^o. 1946, contiennent ce qu'il appelle l' ‘Application des régles de Méchanique au mouvement d'un Vaisseau’. Après avoir traité de la dérive dans le cas d'un ‘Vaisseau poussé par un vent de côté’, il examine, dans l'article 118 en question, l'influence de la situation de la voile sur la vitesse du vaisseau au cas que la direction de la quille reste invariablement perpendiculaire à celle du vent. De même que Renau et Huygens, il suppose la pression du vent sur la voile comme étant proportionnelle au carré du sinus de l'angle d'incidence du vent; quant à la résistance de l'eau contre le mouvement du vaisseau, il ne dit pas expressément de quelle manière il la fait dépendre de la vitesse du vaisseau, mais la construction qu'il donne exige, pour être correcte (laissant de côté la question de la dérive), que cette résistance soit dans la raison simple de la vitesse et non pas, comme Renau et Huygens l'admettaient, dans celle du carré.

11) En effet, dans l'article 119 Pardies n'avait fait que poser un certain nombre de ces propositions, ajoutant seulement que ‘Tout cela se peut résoudre par ces régles de Méchanique; mais’ dit-il ‘je croy que ce qui a été expliqué peut suffire pour le dessein que je m'étois proposé’.

[p. 594]

sur un fondement veritable, & fis faire une seconde impression, qui est celle qui a esté donnée au Public. Mais comme j'estois ocupé à d'autres choses, je laissai par mégarde le mot de force dans la démonstration de l'art. 5 du chap. 2 au lieu du mot de vitesse qu'il saut y substituer¹²⁾; & à quoi M. Huguens n'a pas pris garde. Il est vrai que dans l'art. 6. ch. 1.¹³⁾ je me sers indiferemment des mots de vitesse ou de force, parce que je n'y considere que le mouvement d'un seul corps dans le vuide, & qu'en ce cas la vitesse & la force ont toujours le mesme raport. Je ne me suis aperçu de l'erreur du chap. 7. qu'aprés la seconde édition de mon livre, & dans un temps où mes ocupations ne me permirent pas d'y retoucher. Voici la démonstration qui en marque la fausseté.

Du centre B soit décrit le cercle ADREC, & soit la ligne AB representant la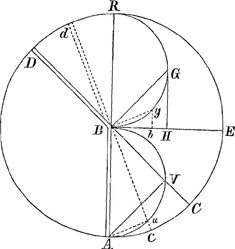



quille du vaisseau, BR la quille prolongée, & sur BR comme diametre soit décrit le demi cercle BGR, & de mesme sur AB le demi cercle ABV, & soit BD une situation du gouvernail, & BC le gouvernail prolongé, BE perpendiculaire sur AB, BG & AV perpendiculaires sur DC, GH perpendiculaire sur BE. Prenant une autre situation du gouvernail comme Bd prolongée en c. Soit tirée dans les mêmes circonstances Bg, Au, & gh. Si le vaisseau se meut en avant suivant la ligne BA, les angles ABC & ABc égaux aux angles GBE & g BE sont les angles d'incidence de l'eau sur le gouvernail. D'où il suit que lors que le gouvernail est dans la situation BD, l'eau frape dans la détermination AV, & avec la vitesse AV, & par consequent avec la force exprimée par le quarré de AV. Et comme la vitesse du vaisseau n'est que comme la racine de la force à cause de la resistance de l'eau, le vaisseau est poussé dans la détermination BG avec une vitesse exprimée par

12) En consultant l'article mentionné on s'aperçoit qu'il s'agit, ici encore, de l'opinion que la décomposition usuelle, suivant des directions perpendiculaires, valable pour les ‘vitesses’ ne le serait pas, sans modification, pour les ‘forces’.

13) Consultez, sur le contenu de ce premier chapitre, la note 4 de la pièce N^o. 2826. A l'art. 6 Renau s'occupe de l'impulsion ou ‘impression’, comme il l'appelle, produite par un petit corps matériel rencontrant obliquement une surface donnée. La ‘vîtesse, ou la force absoluë, avec laquelle ce corps iroit frapper une supersicie perpendiculaire au mouvement’ y est décomposée à la manière usuelle suivant les directions perpendiculaire et parallèle à la surface donnée.

[p. 595]

BG, parce que BG est égale & parallele à AV. Mais lors que le vaisseau est poussé selon BG avec la vitesse BG, il est poussé selon BE avec la vitesse BH. Si le gouvernail estoit dans une autre situation Bd, on verroit par les mesmes raisonnemens que le vaisseau seroit poussé selon BE avec la vitesse Bh. Mais lors que le vaisseau est poussé avec plus de vitesse selon BE, il tourne avec plus de promptitude. C'est pourquoy si BG qui est perpendiculaire à la situation du gouvernail, coupe le demi cercle BGR en deux parties égales, c'est à dire que l'Angle GBE égal à l'angle d'incidence ABC soit de 45. degrez, alors GH perpendiculaire sur BE, sera tangente d'un demi cercle. Ainsi BH qui exprime la vitesse avec laquelle le vaisseau est poussé selon BE, est la plus grande qu'il est possible: car si on met le Gouvernail dans une autre situation comme en Bd, alors Bg qui lui est perpendiculaire, coupera le demi cercle en g, d'où laissant tomber une perpendiculaire en h qui sera plus prés du point B que n'est GH, & le vaisseau sera poussé selon BE avec la vitesse Bh qui sera plus petite que BH. Il en sera de mesme de toutes les autres situations. C'est pourquoy il faut que la barre du Gouvernail BC fasse un angle de 45. degrez avec la quille du vaisseau, pour que le vaisseau tourne le plus promptement qu'il est possible, & non pas comme il est dit dans le VII. Chapitre de la Theorie de la Manoeuvre des vaisseaux, un angle à peu prés de 55. degrez.

M. Huguens finit en disant; Quoyque cette theorie devienne plus difficile aprés la reforme que j'ay indiquée, qu'elle n'estoit dans le traité de M. Renau, je vois toutefois qu'il y auroit moyen de determiner par regle la position du vaisseau & de la voile la plus avantageuse pour gagner au vent, mais la longueur du calcul ne me le permet pas presentement. Outre que la consider ation de la derive du vaisseau n'y seroit pas comprise.

Dans mon traité il n'y auroit rien de si simple que de prouver¹⁴⁾ la position la plus avantageuse de la voile & du vaisseau, non seulement pour gagner au vent, mais mesme pour faire quelque route que ce puisse estre, si la dérive du vaisseau n'y estoit pas comprise. Pour le faire voir, soit la ligne du vent AB¹⁵⁾, & soit donnée une route BK, faisant avec le vent quelque angle que ce puisse estre ABK pour trouver la situation la plus avantageuse de la voile pour que le vaisseau aille le plus viste qu'il est possible dans cete route, suposé qu'il n'eût point de dérive. Prenant BR pour diametre du centre M, soit décrit le demi cercle BGR, & du point M soit tirée MG parallele à la route BK, & du point B au point G soit tiré BG, & soit ensuite tiré DBC perpendiculaire à BG. Je dis que DC est la situation la plus avantageuse de la voile pour aller dans la route BK le plus viste qu'il est possible. Pour le prouver, soit tiré GK perpendiculaire à BK. Par tout ce qui est dit ci-devant, le vent AB pousse le vaisseau par le moyen de la voile DC selon BG avec la vitesse BG, il le pousse selon BK avec la vitesse BK. Et parce que GK

14) Lisez: trouver.

15) Voir la figure de la page suivante.

[p. 596]

est perpendiculaire sur BK, GK sera aussi perpendiculaire à MG. Ainsi GK est tangente au demi cercle. C'est pourquoi toutes les perpendiculaires qu'on menera



de tous les autres points de la circonference de ce demi cercle sur BK tomberont entre B & K. Donc le vaisseau aura plus de vitesse lors que la voile est dans la situation DC que dans toute autre. Et je dis de plus, que la voile DC coupe l'angle ABK, qui est l'angle du vent & de la route en deux parties égales. Pour le démontrer, soit menée MN perpendiculaire sur BG. Cete ligne coupe l'angle BMG qui est égal à l'angle ABK en deux parties égales, & parce que MN est parallele à DC, l'angle BMN qui est la moitié de l'angle BMG égal à l'angle ABK, est égal à l'angle ABC. Donc ce dernier est égal à la moitié de l'angle ABK. D'où il suit qu'il faudroit toujours que la situation de la voile coupast l'angle du vent & de la route en deux parties égales, & que lors que ce seroit pour aller le plus au vent qu'il est possible, il faudroit que le vent fist avec la voile 30. degrez, & la prouë avec la voile aussi 30. d. parce qu'on a démontré dans la theorie de la Manoeuvre¹⁶⁾, que dans quelque situation qu'on mete la voile par raport au vent, il saut que la prouë coupe son complement en deux parties égales; & par cete proposition on voit qu'en quelque situation qu'on mist la prouë, qui est la mesme chose que la route, parce qu'on supose que le vaisseau n'a point de dérive; il faut que la voile coupe l'angle que la prouë fait avec le vent en 2 parties égales. D'où il suit qu'il faudroit que la prouë & la voile coupassent un angle droit en 3. parties égales, c'est a dire que le vent fist avec la voile 30. degrez, la prouë aussi avec la voile 30. degrez, & avec le vent 60.

16) Voir la note 7 de la pièce N^o. 2826.