Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 585]

N^o 2847.
Le Marquis de l'Hospital à Christiaan Huygens.
22 mars 1694.

La lettre se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. Uylenbroek¹⁾.
Elle fait suite au No. 2843.
Chr. Huygens y répondit par le No. 2859.

A Paris ce 22 Mars 1694.

Je vous envoye, Monsieur, la reponce de Mr Renaud²⁾; vous me ferez plaisir de m'en mander vôtre sentiment, je n'ai pas encore eu le loisir de l'examiner, car elle ne vient que de paroistre et de plus la mort de Mr d'Autremonts, oncle de ma femme, m'engage dans beaucoup d'affaires qui ne me laissent quasi point de temps. Je vous prie cependant de m'eclaircir une difficulté qui regarde les developpées.

Mr Bernoulli dans les actes de Leipsic de l'année 1692, page 116³⁾ pretend qu'au point d'inflexion le rayon de la developpée, ou du cercle baisant, devient toujours infiniment grand. Mr Leibnitz, dans la page 443, dit aussi la mesme chose⁴⁾. Or je trouve qu'il peut estre aussi infiniment petit ou zero, car soit une

1) Chr. Hugenii etc. Exercitationes Mathematicae, Fasc. I, p. 313.

2) Cette réponse nous est inconnue dans sa forme primitive d'ouvrage séparé, sous laquelle elle semble être devenue très rare. Pour cette raison nous la reproduisons, dans l'Appendice N^o. 2848 à la présente lettre, telle qu'elle a été réimprimée plus tard dans les numéros du 16 et du 23 mai 1695 du Journal des Sçavans. Lors de cette publication, la réplique de Huygens, que nous donnons plus loin dans cette correspondance, avait déjà paru dans le numéro d'avril 1694 de l'Histoire des Ouvrages des Sçavans. Il est donc bien étrange que dans les numéros cités il ne soit fait aucune mention de cette réplique.

3) Il s'agit de l'article de Jacques Bernoulli qui parut dans les ‘Acta’ de mars 1692 sous le titre: ‘J.B. Additamentum ad Solutionem Curvae Causticae fratris Jo. Bernoulli, una cum Meditatione de Natura Evolutarum, & variis osculationum generibus’, à la fin duquel on trouve le passage qui suit: ‘In omni enim flexu contrario circulus osculator abit in lineam rectam, fit radii infinite magni; quanquam non vicissim, ubicunque circulus osculator infinite magnus est, ibi requiritur flexus in contrarium. In Paraboloidibus omnibus (excepta Parabola communi) circulus osculator verticis infinite magnus, veruntamen non nisi in illis, quorum potestates a numero impari denominantur, flexus contrarius supervenit, caeterae ubique versus easdem partes cavae manent’.

4) Voici le passage en question, tel qu'on le trouve dans l'article cité dans la note 26 de la Lettre N^o. 2819: ‘Sed & hoc notandum est, minimam curvedinem & maximam obtusitatem esse in puncto flexus contrarii, & recte dixit Dn. Bernoullius, circulum osculantem eo casu degenerare in rectam; radius enim est infinitus, seu centrum cadit in lineae evolutae concursum cum sua asymptoto. Quoniam antequam duae proximae, ad curvam perpendiculares, sibi occurentes hactenus ad plagam propositam, fiant sibi occurrentes ad plagam oppositam, seu ex convergentibus divergentes, debent fieri parallelae, quo casu earum concursus infinite abesse debet’.

[p. 586]

ligne courbe BAC, qui ait un point d'inflexion en A, et pour tangente en ce point la droite FAG; il est clair qu'en commençant de developper au point



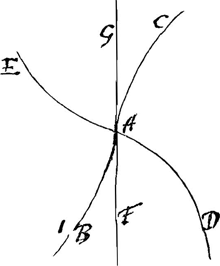A, on decrira la courbe AE par le developpement de la partie CA et la courbe AD par celui de la partie AB:de sorte que la courbe entiere DAE aura aussi un point d'inflexion en A, quoi que dans ce point le rayon de sa developpée BAC soit zero. Supposons par exemple que la courbe EAD soit la paraboloïde aax³==y⁵, qui a un point d'inflexion en A, je puis demontrer que le rayon de sa developpée en ce point sera nul ou zero. La raison qu'aporte Mr Leibnitz dans la mesme pag. 443⁵⁾ ne fait rien contre moi, car avant que deux perpendiculaires à une courbe infiniment proches l'une de l'autre deviennent de convergentes divergentes, il faut necessairement ou qu'elles deviennent paralelles, comme à remarqué Mr Leibnitz, ou bien qu'elles deviennent nulles ou zero ce qu'il n'a point remarqué. Le premier cas arrive lorsque les rayons de la developpée vont en croissant à mesure qu'ils aprochent du point d'inflexion et le second lorsqu'ils vont en diminuant. Mr Bernoulli fait encore ici une faute considerable⁶⁾ lorsqu'il dit que dans toutes les paraboloïdes (excepté la parabole commune) le cercle baisant du sommet est infiniment grand, car il y a une infinité de ces paraboloïdes ou il est infiniment petit. En voici la regle⁷⁾. Soit en general m l'exposant des abscisses et n celui des appliquées (je suppose m moindre que n, afin que ces courbes soient convexes par raport à leurs axes), je dis que si 2m surpasse n le rayon de la developée au sommet est nul, et qu'au contraire si 2m est moindre que n il sera infiniment grand. Je vous en enverrai la demonstration si vous le souhaitez.

Au reste il me paroist evident que Mr Leibnitz se trompe lorsqu'il pretend que les quatre intersections d'un cercle avec une ligne courbe doivent se reunir en une afin que le cercle devienne le plus proche qu'il est possible de la courbe ce

5) Consultez la dernière phrase du passage cité dans la note précédente.

6) Il s'agit de la dernière phrase du passage cité dans la note 3. Remarquons toutefois qu'il nous semble probable que Jacques Bernoulli n'a eu en vue que les paraboloïdes y=axⁿ, où n représente un nombre entier.

7) Elle est exacte; consultez la réponse de Huygens, notre N^o. 2859.

[p. 587]

qu'il appelle baisant⁸⁾: au contraire il est clair, ce me semble qu'il n'y en doit avoir que trois et que le cercle doit alors couper la courbe, comme le pretend Mr Bernoulli⁹⁾.

Faites moi, je vous prie, le plaisir de me mander vôtre pensée sur tout cela.

J'ai ecrit à Mr Bernoulli, comme je vous l'avois marqué¹⁰⁾ pour savoir quel etoit son sentiment sur la courbure de la voile lorsque l'on suppose le nombre des parallelogrammes, qui la composent sini; mais il ne m'a fait reponce que depuis peu et il me mande qu'il n'a point le loisir de songer à ces matieres parce qu'il est sur le point de se faire passer docteur en medecine pour se marier ensuitte. Il me promet cependant qu'après que cela sera passé il me rendra reponce sur cet article. Je ne manquerai pas de vous la faire savoir aussitost¹¹⁾. Je suis tres parfaitement Monsieur vôtre tres humble et tres obeissant serviteur

Le M. de l'Hospital.

8) On rencontre l'erreur en question pour la première fois dans l'article de Leibniz des ‘Acta’ de juin 1686, cité dans la note 3 de la Lettre N^o. 2699. On y lit: ‘Ut autem habeatur & modus inveniendi circulum osculantem, sciendum est, quemadmodum tangentes inveniuntur per aequationes quae habent duas radices aequales, seu duos occursus coincidentes, & flexus contrarii per tres radices aequales; ita circuli vel aliae quaevis lineae datam osculantes inveniuntur per quatuor radices aequales, seu per duos contactus in unum coincidentes’. Et qu'il s'agit ici en effet d'une erreur, et non pas d'une conception différente du cercle osculateur, c'est ce qu'on peut voir en consultant soit la définition de ce cercle, telle qu'on la trouve plus haut dans l'article cité, soit les pages 156 et 157 de la Lettre N^o. 2699, où la même faute est répétée et où l'on aperçoit encore plus clairement son origine, qui consiste en ce que Leibniz considère à tort l'‘osculation’ comme le résultat de la coïncidence de deux contacts. Même après la critique de Bernoulli, que l'on trouve dans l'article cité dans la note 3, Leibniz persistait dans son opinion, prétendant, dans l'article mentionné dans la note 4, que le cas des quatre intersections était le cas général et celui des trois l'exception. Bernoulli répliqua encore dans les ‘Acta’ de juin 1693, aux pages 249-251 de l'article cité dans la note 22 de la Lettre N^o. 2819.

9) A la page 112 de l'article cité dans la note 3. Huygens lui-même était d'ailleurs arrivé depuis longtemps à la même conclusion. Consultez là-dessus la Lettre N^o. 2709 et surtout l'annotation d'octobre 1654 que l'on trouve mentionnée dans la note 6 de cette lettre.

10) Voir la Lettre N^o. 2843.

11) De l'Hospital n'y est plus revenu.