Oeuvres complètes. Tome VII. Correspondance 1670-1675
(1897)–Christiaan Huygens–No 1837.
| |
[pagina 88]
| |
d'esprit. Nous attendons aussi de Messieurs vos colleges plusieurs choses considerables, que l'on nous a fait esperer il y a quelque temps, particulierement la mesure de la terre, l'Anatomie de plusieurs Animaux et la description de quelques Plantes. Vostre Academie, jouissant de toutes les assistances necessaires à executer, fera voir au monde, sans doubte, la force des Esprits Clairvoians, et combien de choses belles et utiles ils peuvent produire. Quant à la Societé Royale, Elle ne s'assemble point à present, ayant commencé sa vocationGa naar voetnoot2) qu'elle a accoustumé de faire dans cete saison. Sans cela, Elle persiste à faire des Experiences autant qu'Elle peut. On espere de pouvoir travailler mieux cy-apres. Quelques uns de ses membres ont depuis peu fait imprimer quelques livres nouveaux: Monsieur Boyle, de l'Estrange rarefaction de l'Air &c.Ga naar voetnoot3). Et de l'Utilité de la Philosophie Experimentelle le 2e volumeGa naar voetnoot4); meditant à present sa response aux objections que Monsieur MoreGa naar voetnoot5) a faitez contre quelques unes de ses Experiences; comme aussi un Traité joly et bien philosophique | |
[pagina 89]
| |
touchant les pierres precieusesGa naar voetnoot6). Monsieur Wallis, quoyque malade de la fievre quarte, a achevé la derniere partie de Son Traite de Motu et MechaniceGa naar voetnoot7), qui sortira de la presse au premier iour. Monsieur Lower a adjousté a son livre de motu Cordis et Sanguinis, un petit discours de Origine CatharriGa naar voetnoot8). Monsieur Willis fait astheur imprimer deux Traitez, l'un de Anima BrutorumGa naar voetnoot9), l'autre de Morbis CapitisGa naar voetnoot10). Monsieur Mercator quelque chose des logarithmesGa naar voetnoot11). De plus, ie ne veux pas vous celer, Monsieur, que i'ay communiquéGa naar voetnoot12) (ce que ie crois n'avoir pas fait contre vostre gré) la construction du Probleme d'Alhaxen (que vous nous envoiatez, il y a quelque temps, imprimée de vostre nouvelle facon)Ga naar voetnoot13) a Monsieur Slusius, qui m'a respondu la dessus bien amplement, et qui semble avoir envie de conferer avec vous sur cete matiere, come vous verrez par la suite, Il dit donc dans sa premiere lettre du 22 novembre 1670Ga naar voetnoot14); Alhazeni problematis constructionem, a Viro Nobissimo ad vos transmissam ut vidi, protinus eandem esse cum meâ suspicabar; at inspectis adversariis meis, non leve discrimen reperi, ut mox videbis. Ne quid tamen dissimulem, cum Domini Hugenii constructionem ad calculos revocarem, eandem omninó mecum Analysin secutum deprehendi; sed cum ex illa duae nascantur effectiones, utraque per hy- | |
[pagina 90]
| |
perbolam circa asymptotos, ille unam, ego alteram, uti faciliorem selegeram. Evidens est autem, nil aliud quaeri hoc problemate (si illud ad terminos meré Geometricos revocemus) nisi, in dato circulo (cujus centrum A, radius AP) punctum aliquod ut P, à quo ductis, ad puncta data EB, inaequaliter a centro A distantia, rectis PE, PB, recta AP producta bisecet angulum EPB. Quod quidem varios casus recipit. Vel enim normalis ex A in rectam EB, nimirum AO, cadit inter E et B, vel ultra B. Si ultra, vel rectangulum EOB aequale est quadrato AO, vel majus, vel minus. De casu aequalitatis videbimus infra: nunc veró tres alios casus eadem feré constructione complectimur. Per tria puncta AEB transeat circulus, ad cujus circumferentiam producatur AO in D: ac, siquidem punctum O cadat inter E et B, recta AO versus O producenda erit; sin ultra B, sitque rectangulum EOB majus quadrato AO, producenda erit versus A: At si rectangulum quadrato minus fuerit, circulus in ipso puncto D, rectam AO secabit. Tum ducta AX parallela EB secante circulum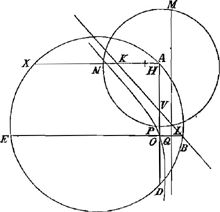 datum in N; fiat, ut rectangulum DAO ad quadratum AN, ita ½ AX ad AH, quae sumenda erit versus X, si O cadat inter E et B, aut rectangulum EOB minus sit 4dto OA, aut ex parte contraria, si sit majus. Ponatur nunc OQ aequalis AH (in directum EB primo et 2do casu, 3to autem versus E). Tum fiant proportionales XA, NA, HK, sumenda omni casu versus X; sectaque AO in V, ut sit eadem ratio KA ad AV, quae AD ad AX; jungatur KV ac producatur donec occurrat rectae QM, parallelae OA 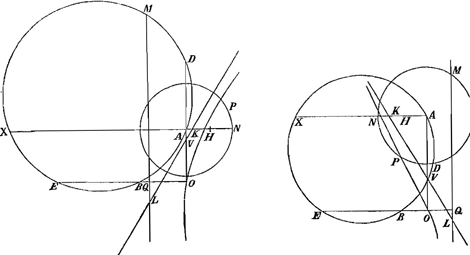 | |
[pagina 91]
| |
indefinite productae, in puncto L; erunt omni casu KL ad QL asymptoti hyperbolae, quae per punctum O descripta, proposito satissaciet: hoc tantum discrimine, quod 1o et 2o casu hyperbola per O, problema solvet in speculo convexo, sectio vero ei opposita in concavo: At 3o casu contrà, hyperbola per O serviet concavo, ejus opposita convexo. Atque id quidem, cum punctum V cadit inter A et O; nam si ultra O caderet, unica hyperbola inter easdem QL, KL descripta tam speculo convexo quam concavo satisfaceret. Caeterum si V caderet in ipsum punctum O, problema tunc planum esset, et ipsae rectae LQ, LK illud absolverent. Unde patet, problematis hujus dari casus infinitos, qui per locum planum solvi possunt, quò magis veniâ digni videntur ii, qui illud per eundem locum universe solvi posse censuerunt, quòd ipsis aliquoties calculus feliciter cecidisset. Nulla enim dari potest trium punctorum AEB positio (de casu aequalitatis rectanguli EOB et quadrati OA mox videbimus), quae non admittat circulum aliquem ex centro A describendum, ad cujus circumferentiam Problema per locum planum solvi queat. Hujus autem circuli radius si tanti est, ita invenietur. In 1o et 2o casu superioris constructionis fiat ut quadratum AX una cum duplo rectangulo OAD, ad duplum quadratum AD, ita quadratum AO ad quadratum AN, erit AN radius quaesitus: at in 3o casu, faciendum est ut quadratum AX minus 2plo rectangulo OAD, ad duplum quadratum AD, ita quadratum AO ad quadratum AN. Construendus nunc superest alius casus, aequalitatis nempe rectanguli EOB et quadrati AO, sive in quo circulus per puncta A, B, E descriptus tangit rectam AO. Rectè autem monuit Clarissimus HugeniusGa naar voetnoot15), hoc casu describendam esse parabolam. Quod tamen non ita intelligendum, quasi per hyperbolam solvi non possit, cum et hyperbolam et ellipsin imò infinitas (si quis methodo nostrâ uti velit) admittat: sed quod parabolam quoque recipiat, quam alii casus respuunt. Eadem ratione temperandum est quod ait, constructionem suam omni casu quo Problema solidum est, locum habere; intelligit enim, levi mutatione inveniri hyperbolam quae proposito serviat; quod casus, à nobis superius constructos cum ejus constructione comparanti planum fiet. Ut autem ad casum Aequalitatis redeam, et ne quid temere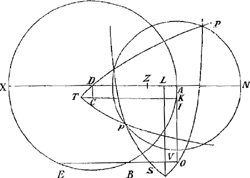 asseruisse videar, ecce Tibi non unam, sed duas parabolas, ac praeterea hyperbolas appositas quae propositum absolvunt. Sint ut prius puncta data EB, circulus e centro A, ac alius per 3 puncta AEB, cujus tangens sit AO centrum D; ductâ diametro NADX, fiant tres proportionales XA, NA, ZA, cujus dimidium sit AL; fiant iterum tres proportionales 2 OA, NA, IA, cujus | |
[pagina 92]
| |
dimidium sit KA, et perficiatur rectangulum LAOV; productaque LV in S, donec VS sit tertia proportionalis ipsarum AI, OV; axe SL, latere recto AI, vertice S, describatur parabola; haec enim circulum secabit in punctis PP quaesitis. Tantundem faciet alia, si perfecto rectangulo DAKLGa naar voetnoot16), et producta KC in T, ita ut CT sit tertia proportionalis ipsarum AZ, DC; describatur circa axem TK, vertice T, latere recto ZA; occurret enim circulo in iisdem punctis PP. 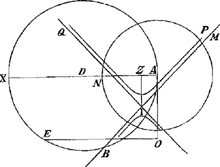 Facilior adhuc est constructio per sectiones oppositas; factis enim, ut prius, tribus proportionalibus XA, NA, ZA, demittatur ZI normalis, tertia proportionalis duplae AO et AN: erit itaque ZI major ZA, cum 2pla AO minor sit XA: tum in puncto I, inclinentur utrinque angulo semi-recto ad lineam IZ, rectae IQ, IM, et ab utraque parte indefinite producantur. Demum circa illas tanquam asymptotos describatur per A hyperbola, et alia ipsi opposita; haec enim satisfaciet problemati in speculo convexo, illa in concavo. Cum vero, ut ostendimus, ZI semper major sit recta ZA, recta IM nunquam transibit per A. Non dabitur itaque casus, quo ex hac constructione velut in praecedentibus, Problema per ipsas asymptotos solvi possit. Et tamen hoc quoque aliquando locum planum admittit; cum scilicet accidit, ut recta ex O ducta ad centrum D tangat circulum NPP; ipsum enim punctum contactus quaestionem solvit. Et hoc quidem de problemate, quod hactenus multorum ingenia exercuit, et cujus solutionem ante aliquot annos absolvi, urgente C.M.V. Gutiscovio Lovaniensi matheseos professore, qui sibi usui futurum ajebat; moliebatur enim nescio quid in Catoptricis; sed mors manum injecitGa naar voetnoot17); neque enim (ut hoc obiter addam) quicquam hujusmodi in schedis ejus repertum intellexi. Jusques icy Monsieur Sluse dans sa 1re lettre; dans l'autre du 9me mars 1671Ga naar voetnoot18) il dit; Quod ad Alhazeni Problema attinet, ut δευτέραι φροντίδες esse solent ἀμείνονες, duas alias ejusdem Analyseos, priori ad te antehac a me missa faciliores, et constructione inter se et ab illa diversas nuper inveni, quin imo praeparationem quandam generalem ex qua Problematum omnium, quae ad punctum reflexionis in speculis sphaericis concavis et convexis determinandum spectant, analysis facilè deduci potest. Sed haec, et meliora acutissimo Hugenio jam occurrisse mihi persuadeo, qui me majorem in hoc argumento operam posuit. Si tamen nugas quoque nostras videre vellet, libenter cum ipso communicarem. | |
[pagina 93]
| |
Vous voiez, Monsieur, la franchise de ce grand homme; vous en userez selon vostre discretion, et, si vous ne luy escrivez pas vous mesme sur ce sujet, m'instruirez, s'il vous plait, de ce que ie luy respondray là dessus. Je me croiois aucunement obligé de vous faire scavoir tout ce qui s'est passé entre luy et moy en cete matiere; ce qu'ayant fait, vous aurez assez de bonté, de pardonner cete prolixité, puisque i'ay eu assez de patience de transcrire tout cela de ma propre main, ne m'y osant fier à mon copiste. J'ay mis icy les dernieres TransactionsGa naar voetnoot19): Monsieur vostre Pere a eu quelques unes des precedentes, que, peut estre, il vous a desia envoyez. Vous prendrez tout en bonne part de Monsieur Vostre tres humble et tres obeissant Seruiteur Oldenburg.
Quand on m'escrit par la poste, on continue tousiours cete adresse,
A Monsieur Monsieur Grubendol. à Londres. Rien que cela.
A Londres le 22 juillet 1671. PS. Dans les TransactionsGa naar voetnoot20) prochaines on mettra la responce de Monsieur WallisGa naar voetnoot21) au livre nouveau de Monsieur HobbesGa naar voetnoot22), dont il est parlé dans celles, qui sont encloses icy. A Monsieur Monsieur Christian Hugens de Zulichem, a Paris. |
|

