Oeuvres complètes. Tome VI. Correspondance 1666-1669

N^o 1669.
Christiaan Huygens à J. Gallois.
12 novembre 1668.

La copie se trouve à Leiden, coll. Huygens¹⁾.
La lettre a été publiée dans le Journal des Scavants du 12 Nov. 1668.
Elle est une répouse au No. 1653. Gregory y répondit par le No. 1682.

La recherche de la Quadrature du Cercle a fait trouver tant de belles choses aux Geometres, qu'afin qu'ils ne soient pas privez d'un exercice si utile, je suis d'avis de defendre contre Monsieur Gregory la possibilitè d'y reüssir: Et je n'aurois pas attendu si long temps à donner cette replique, si à l'occasion de nostre dispute je ne m'estois laissè aller à un examen tres exact de ce qui regarde la mesure

1) Quoique la copie contienne quelques variantes, nons avons cru devoir publier cette lettre d'après le texte du Journal des Scavans.

[p. 273]

approchante du Cercle et de l'Hyperbole; en quoy j'ay estè interrompu plusieurs fois par d'autres occupations.

Je dis donc premierement, pour ce qui regarde l'impossibilitè analytique de la Quadrature de ces Figures, que tant s'en faut, mesme apres le supplement²⁾ que Monsieur Gregory a donnè à ses demonstrations, que cette impossibilitè soit bien prouvée; qu'il demeure encore incertain si le Cercle et le Quarrè de son diametre ne sont pas commensurables, c'est à dire à raison de nombre à nombre; et de mesme en ce qui est d'une portion determinée de l'Hyperbole, et de sa figure rectiligne inscrite.

Et pour le faire voir, il suffit de remarquer que sa Proposition XI et son supplement ne prouvent rien lors qu'on determine les quantitez a et b dans sa progression convergente par des nombres rationels ou sourds; parce qu'alors la terminaison pourra aussi estre quelque nombre semblable, sans qu'on puisse demontrer le contraire par cette Proposition, d'autant qu'on ne pourra dire de quelle façon la terminaison est composée des premiers & des seconds termes. Par exemple, si a est 1; et b, 2; comment prouvera t on par sa Proposition XI que la terminaison n'est pas 3/7? Pour conclure donc que la raison du Cercle au Quarrè de son diametre n'est pas analytique, il falloit demontrer non seulement que le Secteur de Cercle n'est pas analytique indefinitè à sa figure inscrite, quoyque cette demonstration ne laisse pas d'avoir sa beautè; mais que cela est vray aussi in omni casu definito.

Je dis de plus, que les quantitez a et b demeurant indeterminées, la terminaison se reduira peut-estre à quelque equation de celles dont on ne peut pas donner la racine; sans que le contraire se puisse prouver par sa Proposition XI ny par son supplement: Et neantmoins si cette terminaison estoit reduite à quelque equation de cette nature, je croirois que la Quadrature seroit trouvée geometriquement; et le Probleme se pourroit resoudre par l'intersection de quelques lignes courbes qu'on reçoit en Geometrie.

Je n'insisteray pas sur les autres objections que j'ay proposées. Je diray seulement que comme elles n'ont plus de lieu apres les corrections que Monsieur Gregory a faites; aussi elles estoient bien fondées auparavant, parce qu'ayant omis la division si necessaire par a - b en tant d'endroits de sa Proposition VII on pouvoit presumer qu'il ne scavoit pas qu'elle fust possible, et que par consequent il avoit cru qu'il estoit necessaire d'admettre des quantitez indefinies dans la composition dont il s'agit.

Je passe donc à la comparaison de nos methodes pour la dimension approchante du cercle. Il est certain que ses premieres approximations fondées sur sa Propo-

2) Consultez la Lettre N^o. 1653 et le Prooemium de la Geometriae Pars Universalis, 1668, cité dans la Lettre N^o. 1605, note 4.

[p. 274]

sition XX et XXI sont les mesmes que j'avois données dans mon Traitè de Circuli magnitudine³⁾, où j'ay demontrè ces mesmes Theoremes, sçavoir que si le Polygone inscrit au cercle, est a; et le Polygone circonscrit semblable, d; le contenu du cercle est moindre que ⅓ a + ⅔ d mais plus grand que 4/3 c - ⅓ a, posant c pour un Polygone inscrit de deux fois autant de costez que a ou d. Ce que je dis icy, et ce que je diray encore cy-apres du cercle, se doit entendre de mesme du secteur de cercle.

Outre cette approximation, Monsieur Gregory en propose une autre à la fin de sa Proposition XXV, qu'il dit estre admirable, mais dont il avoüe qu'il ne sçait pas la demonstration. C'est qu'entre les deux termes que je viens de mettre ⅓ a + ⅔ d, et 4/3 c - ⅓ a ayant trouvè quatre quantitez moyennes en proportion Arithmetique, il dit que la plus grande de ces quantitez approche si pres de la grandeur du cercle, que si les nombres qui designent les Polygones semblables a et d, ont le premier tiers de leurs chiffres semblable l'un à l'autre, il n'y aura pas une unitè à dire à la veritable mesure.

Mais je trouve que cette approximation n'est pas vraye dans le cercle, quoy qu'elle le soit dans l'Hyperbole; et que comme dans celle-cy il prend la plus grande des quatre moyennes Arithmetiques, il faut prendre la plus petite pour l'approximation du cercle.

Ainsi la moindre des quatre moyennes entre les termes susdits de la premiere approximation, sera 16 c + 2 d - 3 a / 15 comme il est aisè de veoir par le calcul; et je puis prouver non seulement par experience, mais encore par la demonstration que les Polygones a et d s'accordant jusqu'au tiers de leurs chiffres, ce dernier terme ne peut differer au plus de la veritable grandeur du cercle, que dans les deux derniers chiffres; et que le plus souvent il doit avoir tous les mesmes et au delà; qu'il excede pourtant le cercle; et qu'au contraire la plus grande des quatre moyennes dont se sert Monsieur Gregory dans l'Hyperbole, est deficiente.

J'ay trouvè de plus, que cette approximation pour le cercle n'est pas encore si precise que celle qui est dans mon Traitè de Circuli magnitudine, suivant laquelle lors qu'a, c et d signifient les mesmes Polygones que dessus, le terme excedant le contenu du cercle est a + 10 cc - 10 aa / 6 c + 2 a. Et la demonstration n'en est pas difficile: parce que si l'on vouloit dire que ce terme n'est pas moindre, ny par consequent plus precis que le precedent 16 c + 2 d - 3a / 15, il s'en suivroit que le cube

3) Voir l'ouvrage cité dans la Lettre N^o. 191, note 1.

[p. 275]

de c - a ne seroit pas plus grand que rien, et c pas plus grand que a, contre ce qui est supposè, comme il est aisè de voir par le calcul analytique en prenant garde que d est esgal à a / cc.

On peut aussi prendre a et c pour les circonferences des Polygones inscrits dont l'un a la moitiè autant de costez que l'autre. Et alors le terme a + 10 cc - 10 aa / 6 c + 9 a est la longueur de la circonference du cercle ou de l'arc du Secteur, l'excedant de si peu, que si le tiers des chiffres en a et c est le mesme, il ne peut jamais estre different de la veritable longueur que dans le dernier chiffre, et le plus souvent il la doit suivre encore dans quatre ou cinq chiffres outre le nombre de ceux qui composent a ou c.

Mais afin que ceux qui n'entrent pas dans toutes ces speculations, ne laissent pas de tirer quelque profit de nostre dispute; j'ajouteray icy une construction Geometrique tirée de cette derniere approximation, pour trouver la longueur d'un arc de cercle donnè, aussi pres que l'on peut souhaiter pour l'usage.

Soit l'arc de cercle, qui n'excede point la demi-circonference, ABC, dont la soutendante soit AC; et l'un et l'autre soit divisè en deux parties esgales par la ligne BD.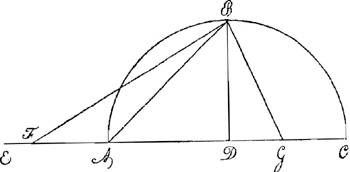

Ayant tirè la soustendante AB, il faut en prendte le ⅔, et les mettre depuis A jusqu'en E dans la ligne CA prolongée. Puis ayant diminuè la ligne DE de sa dixiesme partie EF, il faut mesner FB, et enfin BG, qui luy soit perpendiculaire: et l'on aura la ligne AG esgale à l'arc AB; ou sa double, à l'arc ABC, qui excedera de si peu, que lors mesme que cet arc sera esgal à la demy-circonference du cercle, il n'y aura pas à dire 1/1400 de sa longueur; mais s'il n'est que d'un tiers de la circonference, il n'y aura pas 1/13000 de difference; et s'il n'est que d'un quart, il ne s'en faudra pas 1/90000 de sa longueur.

Je pourrois ajouster une approximation et une construction toute semblable pour la quadrature de l'Hyperbole, un peu plus approchante de la veritable, que la moyenne Arithmetique de Monsieur Gregory dont j'ay parlè cydessus: mais je craindrois de trop estendre cet escrit; et je suis persuadè d'ailleurs qu'apres ce que

[p. 276]

Monsieur Mercator⁴⁾ a depuis peu heureusement trouvè⁵⁾ touchant cette quadrature, et la reforme⁶⁾ que Monsieur Wallis y a faite, ce que nous avons jusqu'icy trouvè sur ce sujet, n'est plus gueres considerable.

4) Sur Nicolaas Mercator, voir la Lettre N^o. 201, note 8.

5) Logarithmo-Technia; sive Methodus construendi Logarithmos, nova, accurata, & facilis; Scripto Antehàc Communicata, Anno Sc. 1667. Nonis Augusti: Cui nunc accedit Vera Quadratura Hyperbolae & Inventio Summae Logarithmorum. Auctore Nicolao Mercatore Holsato, è Societate Regia. Huic etiam jungitur Michaelis Angeli Riccii Exercitatio Geometrica de Maximis & Minimis; hîc ob Argumenti praestantiam & Exemplarium raritatem recusa. Londini, Typis Guilielmi Godbid, & Impensis Mosis Pitt Bibliopolae, in vico vulgò vocato Little Britain. Anno m.dc.lxviii. in-4^o.
Il existe une réimpression de cet ouvrage, publiée à Londres. 1674. in-4^o.

6) Consultez les Philosophical Transactions du 17 août 1668 N^o. 38, page 753.