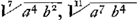Oeuvres complètes. Tome VI. Correspondance 1666-1669

[p. 240]

N^o 1653.
J. Gregory à H. Oldenburg.
23 juillet 1668.

La pièce a ètè imprimèe dans les Philosophical Transactions No. 37, du 13 Juillet 1668 [V. st.].
Elle est une réponse au No. 1647. Chr. Huygens y répondit par le No. 1670.

Mr. Gregories Answer

To the Animadversions of Monsieur Hugenius upon his Book, De vera Circuli & Hyperbolae Quadratura; as they were publish'd in the Journal des Scavans of July 2. 1668¹⁾.

This Answer we shall give the Reader in the same Language and Words, in which the Author of it desired, it might be inserted in this Tract, viz.

Ad ea quae dicit Dominus Hugenius contra meam Circuli & Hyperbolae Quadraturam, ingenue fateor (cum illa scriberem) me non animadverisse exemplum in propositione 10. non esse seriem convergentem; experientiam enim feci solummodo de primis & secundis terminis, non considerando tertios cum primis conincidere; nam ratiociniis insistebam, de exemplis parum solicitus: Ut autem appareat in hoc nihil contineri contra nostram Doctrinam, agedum hoc loco 10. propositionem totidem verbis, sed cum legitimo exemplo, repetamus.

1) Voir la pièce N^o. 1647.

Propositio 10. Problema.

Ex data quantitate codem modo composita a duobus terminis convergentibus cujuscunque seriei convergentis, quo componitur ex terminis convergentibus immediate sequentibus; seriei propositae terminationem invenire.

Sit series convergens, cuius duo termini convergentes quicunque sint a, b, & termini convergentes immediate sequentes 2a b/a+b, a+b/2; termini priores inter se multiplicati essiciunt ab, item sequentes inter se multiplicati essiciunt eandem ab, ex his invenienda sit propositae seriei terminatio. Manifestum est, quantitatem ab eodem modo sieri a terminis convergentibus a, b, quo a terminis convergentibus immediate sequentibus 2a b/a+b, a+b/2: & quoniam quantitates a, b, indesinite ponuntur pro quibuslibet totius seriei terminis convergentibus, evidens est, duos quoscunque terminos convergentes propositae seriei inter se multiplicatos

[p. 241]

idem essicere productum, quod faciunt termini immediate sequentes etiam inter se multiplicati; cumque duo termini convergentes duos terminos convergentes semper immediate sequantur, manifestum est, duos quoscunque terminos convergentes inter se multiplicatos idem semper essicere productum, nempe ab, atque ultimi termini convergentes sunt aequales, & proinde sit ultimus ille terminus, seu seriei terminatio z, quae in seipsum multiplicata facit z²=ab; est igitur z, seu scriei terminatio r² ab²⁾, quam invenire oportuit: & proinde ad inveniendam cujuscunque seriei convergentis terminationem opus est solummodo invenire quantitatem eodem modo compositam ex terminis convergentibus primis, quo componitur eadem quantitas ex terminis convergentibus secundis.

2) r² ab s'écrit actuellement √ab, et de même les notations r⁷ a⁴ b², r¹¹ a⁷ b⁴ désigent .

Consectarium.

Quoniam non refert in Problemate, sive termini convergentes, a, b, sint primi, secundi vel tertii, &c. manifestum est, omnis seriei convergentis terminationem eodem modo esse compositam ex terminis convergentibus primis, quo ex secundis, tertiis, &c.

Si quis aliud exemplum desideret, sint primi termini a, b, secundi r⁷ a⁵ b²²⁾, r² ab, quantitas eodem modo composita &c. est a⁷ b⁴ & feriei terminatio r¹¹ a⁷ b⁴²⁾: videat Hugenius, duo exempla legitima hic adducta inquisitionem septimae non admittere; ope tamen propofitionis decimae (supposita tertia illa quantitate) facile resolvuntur, neque ullo modo consectarium respuunt, quod solummodo esse momenti satis sit indicasse; plura autem exempla desideranti millena afferam.

Ad primam Hugenii objectionem quod spectat, miror eum non considerasse praecedens consectarium, ubi illa, quae desiderat, evidenter deduco ex propositione 10. At agnoscit hoc verum esse in illis seriebus, quae ope nostrae methodi terminantur: velim certe ut assignet mihi Nobilissimus vir seriem aliquam convergentem cum sua terminatione, quae consectarium nostrum respuat; vel si eam assignare non possit, solidam dubitandi rationem tantum desidero. Ut autem funditus evertatur haec objectio, sequentem exhibeo demonstrationem Geometricam.

Sit A. polygonum regulare sectori inscriptum, B. eidem simile circumscriptum; continuetur series convergens polygonorum &c. ut sit ejus terminatio seu circuli sector z³⁾: sit x⁴⁾ eodem modo composita à terminis C, D, quo z³⁾ à terminis A, B; dico z³⁾ & x⁴⁾ esse indefinite aequales; si non sint indesinite aequales, sit inter illas indesinita differentia a, & continuetur series convergens in terminos convergen-

2) r² ab s'écrit actuellement √ab, et de même les notations r⁷ a⁴ b², r¹¹ a⁷ b⁴ désigent .

2) r² ab s'écrit actuellement √ab, et de même les notations r⁷ a⁴ b², r¹¹ a⁷ b⁴ désigent .

3) Lisez: Z.

4) Lisez: X.

3) Lisez: Z.

3) Lisez: Z.

4) Lisez: X.

[p. 242]

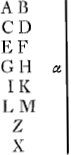tes I, K, ita ut eorum differentia sit minor quam α; hoc enim absque dubio concipi potest, etiamsi hic omnes quantitates sint indesinitae, quoniam definitis quantitatibus A, B, definitur etiam α, sed adhuc restat K-I quantitas indeterminata in infinitum decrescens. Manifestum est, sectorem z⁵⁾ esse indefinite minorem quam K, & majorem quam I: item quoniam Z eodem modo componitur ex quantitatibus A, B, quo X e quantitatibus C, D, & z⁵⁾ indesinite minor est quam K & major quam I, patet ex proprietatibus serierum convergentium, X etiam esse indefinite majorem quam I, & minorem quam K (est enim revera indefinite major quam L & minor quam M) & proinde sunt quatuor quantitates indefinitae, quarum maxima & minima sunt I, K, intermediae autem Z & X, & ideo differentia extremarum K-I major est quam α differentia mediarum, quod est absurdum, ponitur enim minor; quantitates ergo Z & X non sunt indesinite inaequales, & ideo sunt indefinite aequales, quod demonstrandum erat. Manifestum est hanc demonstrationem eodem modo applicabilem esse omni seriei convergenti.

In objectionibus 2, 3 & 4, contra suas ipsius imaginationes argumentatur Hugenius; Ego enim satis dilucide affirmo in scholio propositionis 5, et in fine propositionis 9. septimam & nonam propositionem esse particularem, unamquamque suo casui; item in propositione decima (quam ergo pro generali substituo) evidenter suppono, & non quaero, illam quantitatem eodem modo compositam ex primis, quo ex secundis terminis convergentibus; satis enim scio, talem methodum generalem esse impossibilem. Sed omnium maxime admiror, Clarissimum virum non animadvertisse in 8 definitione, Quantitates C, D, E, compositionem ingredientes, semper esse easdem, nempe definitas & invariabiles, ipsos autem terminos A, B. esse indefinitos & variabiles, nimirum in F, G, & infinitos alios: at quis est qui non videt, Hugenii b²m/a²+ba non minus esse indefinitam, quam sunt ipsi termini? Deinde in Prooemio nostrae Geometriae partis universalis⁶⁾, sic dico. Alii objiciunt contra propositiônem 11. ita; si addatur a³ termino a³+a²b & termino ba²+b²a, enervetur vis utriusque demonstrationis. Respondeo, a³ esse quantitatem indefinitam, & alias quantitates indefinitas praeter ipsos terminos convergentes compositionem non posse ingredi, quod analystam laiere non potest: Eodem modo respondeo Hugenio, bbm/a²+ab esse quantitatem indesinitam & ideo compositionem non posse ingredi. Si autem mihi objiciat, in septima me credidisse, mae-mbe/ad-bd fuisse quantitatem indefinitam; Respondeo, etiamsi divisio per a-b à me satis inconsiderate

5) Lisez: Z.

5) Lisez: Z.

6) Consultez l'ouvrage cité dans la Lettre N^o. 1605, note 4.

[p. 243]

neglecta sit, aperte tamen constat, me hoc cognovisse, ex diversitate methodorum, quibus utor in septima & decima, quippe ista particulari, in qua quantitatem illam quaero, & hac generali, in qua illam suppono; nulla enim alia ratio hujus diversitatis excogitari potest; quod etiam ex ipsis septima & decima est manifestum, cum appellem semper terminos convergentes quantitates indefinitas, hoc ipso satis significans, nullas alias quantitates indefinitas calculo inesse.

Semper credidi in rebus scientificis verba ita candide esse explicanda (si modo possibile sit) ut discursus nullum includat absurdum; at Hugenius satis percipit, discursum nihil continere absurdi, modo nulla quantitas indefinita praeter ipsos terminos compositionem ingrediatur; judicat tamen absque omni ratione, me contrarium existimasse; libenter enim optarem Hugenium assignasse locum, ubi assero, illam inquisitionem 7^mae esse universalem. Dico igitur & declaro me intelligere, nullam quantitatem indefinitam praeter ipsos terminos convergentes compositionem posse ingredi. Atque ita corruunt tres ultimae Hugenii sive diversae objectiones, sive ejusdem portiones; nescio enim, quare in tot partes dividatur.

Praecedentibus perceptis, evidentissimum est, Circuli, Ellipseos vel Hyperbolae Sectorem esse terminationem seriei convergentis⁷⁾, cujus primi termini a³+a²b, ab²+b³, & secundi ba²+b²a, ² b²a⁸⁾, & proinde Sectorem eodem modo componi⁹⁾ ex primis terminis quo ex secundis; atque evidens est, nullam dari quantitatem eodem modo analyticè compositam ex primis terminis quo ex secundis, quoniam primos eodem modo analyticè tractando quo secundos, semper restat altior potestas ipsius a in primorum producto, quam in producto secundorum; de hoc (si non credatur) siat experientia, & constabit non solum assertionis veritas, sed etiam ejusdem demonstratio; quando autem altior est ejusdem potestas in una quantitate quam in altera, nulla datur indefinita aequatio, de qua hic tantum loquimur, hoc est, ut (positis a, b, ad libitum) aequalitas semper ritè procedat. Atque haec est summa non solum propositionis 11^mae sed etiam totius nostrae Circuli & Hyperbolae Quadraturae, ad Hugenio adhuc intactae. Gratias tamen ago nobilissimo viro, quod meas qualescunque lucubrationes examinare dignatus est, hinc enim mihi data est occasio illas fusius explicandi & confirmandi. Num Hugeniana methodus circulum mensurandi mea sit praecisior, experientiae relinquo judicandum; quod autem nostra, Hyperbolam quadrandi, illi etiam innotuerat, de hoc nihil habeo quod dicam, nisi quod mihi gratuler, inventa mea ipso Hugenio non aestimari indigna.

7) En marge: Scholium 5. [J. Gregory].

8) Lisez: 2b²a.

9) En marge: Consectarium 10. [J. Gregory].