Oeuvres complètes. Tome X. Correspondance 1691-1695
(1905)–Christiaan Huygens–
[pagina 630]
| |||||||||
No 2861.
|
| AD ∞ x | BD sive DH ∞ y x3+y3 ∞ nxy |
| AN ∞ z, | |
| NH ∞ t, | z-t/√2 ∞ x, t2∞z2Ga naar voetnoot3) M.Ga naar voetnoot4) -2z+n√2/6z+n√2,  |
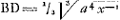 |
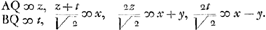
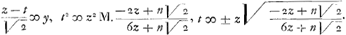 |
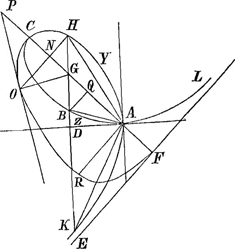
Laet beschreven worden de kromme CORF, wiens diameter is CF, ende de ordinatim applicata NO; de natuure van deze kromme is soodanigh dat de intercepta tusschen de ordinatim applicata NO en de perpendiculaer op de kromme OG, naementlijck NG, zoo groot is als de ordinatim applicata van de kromme CHA te weten NH Qu. [aeritur] de aequatie, die de natuur van de kromme CORF denoteert, te vinden.
NG is dan volgens het gesupponeerde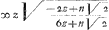 . de regel
. de regel
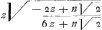 met z wederom moeten werden gemultipliceert, om z te brengen tot dezelfde dimensien, die in de aequatie van de kromme gevonden worden; komt
met z wederom moeten werden gemultipliceert, om z te brengen tot dezelfde dimensien, die in de aequatie van de kromme gevonden worden; komt 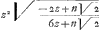 maer om deze quantiteijt te brengen tot een andere, waarin geen termen ten respecte van z zullen ontbreecken, zoo laet in plaets van zz gestelt wordenGa naar einda) az2+bz+c (a, b en c zijn quantiteijten, waermedeider term zal geafficieerd moeten worden),
maer om deze quantiteijt te brengen tot een andere, waarin geen termen ten respecte van z zullen ontbreecken, zoo laet in plaets van zz gestelt wordenGa naar einda) az2+bz+c (a, b en c zijn quantiteijten, waermedeider term zal geafficieerd moeten worden), 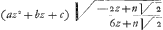 kan nu gelijck gesupponeert worden aen u2; NO gestelt zijnde=u, want
kan nu gelijck gesupponeert worden aen u2; NO gestelt zijnde=u, want 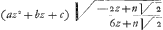 moet geconsidereerd worden als te zijn maer van 2 dimensien, en CF is gesteld geweest te zijn de diameter van de kromme CORF; zoo is dan
moet geconsidereerd worden als te zijn maer van 2 dimensien, en CF is gesteld geweest te zijn de diameter van de kromme CORF; zoo is dan 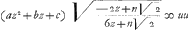 . En van het surdise getal gelibereert, en de termen aan eene zijde gebraght zijnde:
. En van het surdise getal gelibereert, en de termen aan eene zijde gebraght zijnde:
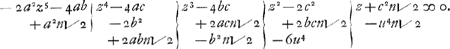
hieruijt wort door den regel van SlusiusGa naar voetnoot5) gevonden
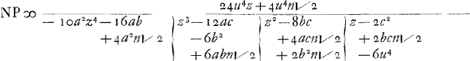 NP is mede ∞
NP is mede ∞ 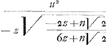 ; want gelijck GN tot NO, also NO tot
; want gelijck GN tot NO, also NO tot
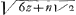 M.-z√(-2z+n√2)
M.-z√(-2z+n√2)
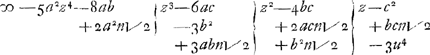
en in plaats van u2 en u4 haere valeuren gestelt.
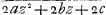 M.
M. 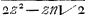
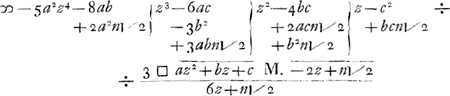
ende door de multiplicatie komt.
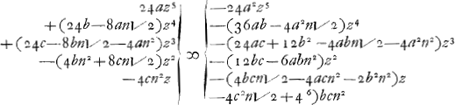
de termen van de aequatie met malkanderen vergelijckende is
24 az5 ∞-24 a2z5 en a ∞-1
verders is (24b-8an√2) z4 ∞ (-36ab+4a2n√2)z4,
en in plaets van a gestelt-1 komt b ∞+⅓n√2 en+4c2n√2 ∞+4Ga naar voetnoot6) bcn2, en in plaets van b gestelt ⅓ n√2 komt c ∞ ⅙ n2 deze valeuren van a, b, c dan gestelt in d'aequatie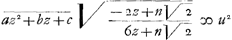 komt
komt 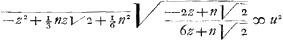 voor de aequatie van de kromme CORF, z zijnde=AN en NO=u, uyt welke aequatie de natuur van deze kromme openbaer genoegh is, want de ordinatim applicata NO ofte u wordende gestelt ∞ 0, komt z ∞ ½n√2 en z ∞-⅙n√2 tot een teecken dat de kromme de linie CF zal snijden in C en F want AC is ∞ ½ n√2 en AF=-⅙n√2 met het signum - omdat F aen d'andre zijde contrary als C wort genomen, zoo dat AF dan ⅓ is van AC door welk punt F oock loopt d'a symptotos van het blatie AHCBAL. dewijle nu de linie NG ∞ NH is zoo zal volgens het theorema
voor de aequatie van de kromme CORF, z zijnde=AN en NO=u, uyt welke aequatie de natuur van deze kromme openbaer genoegh is, want de ordinatim applicata NO ofte u wordende gestelt ∞ 0, komt z ∞ ½n√2 en z ∞-⅙n√2 tot een teecken dat de kromme de linie CF zal snijden in C en F want AC is ∞ ½ n√2 en AF=-⅙n√2 met het signum - omdat F aen d'andre zijde contrary als C wort genomen, zoo dat AF dan ⅓ is van AC door welk punt F oock loopt d'a symptotos van het blatie AHCBAL. dewijle nu de linie NG ∞ NH is zoo zal volgens het theorema
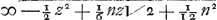 M. met
M. met 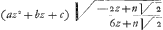 . Dit getrocken van 1/12 n2 komt voor ANHYA
. Dit getrocken van 1/12 n2 komt voor ANHYA
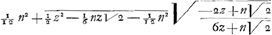 ; en het triangel ; en het triangel |
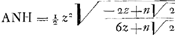 hier van getrocken, voor het spatium AHYA,
hier van getrocken, voor het spatium AHYA,
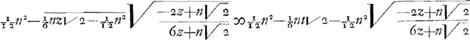
in de plaets van z nu gestelt zijnde ½ x √2+½y√2 (gelijck z gevonden is) komt
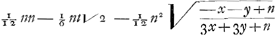 en voor, n, genomen x3+y3/xy
en voor, n, genomen x3+y3/xy
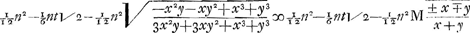
y genomen zijnde grooter als x, 't welk geschiet wanneer wij AN ∞ z stellen, komt voor het spatium AHYA
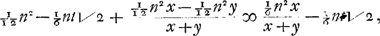 |
en in plaets van t gestelt sijne valeur ½y√2-½x√2,
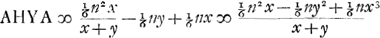 |
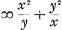 , AHYA
, AHYA 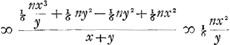 maer x grooter zijnde als y, naementlijck wanneer AQ ∞ z gestelt is zoo zal het spatium ABZA ∞ zijn
maer x grooter zijnde als y, naementlijck wanneer AQ ∞ z gestelt is zoo zal het spatium ABZA ∞ zijn 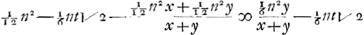 en in plaets van t gestelt sijne valeur ½x√2-½y√2
en in plaets van t gestelt sijne valeur ½x√2-½y√2
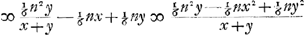 en, n, zijnde
en, n, zijnde 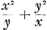 ,
,
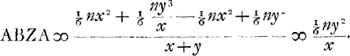 |
- voetnoot1)
- Cet Appendice, sur l'origine duquel on peut consulter la note 19 de la Lettre No. 2859, contient une solution du problème de la quadrature du folium de Descartes. Pour en faciliter la lecture nous croyons faire bien en faisant suivre ici un aperçu de la méthode employée: Après avoir déduit l'équation
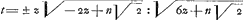 de la courbe, rapportée aux axes AC et AR, où AN=z, NH=t, l'auteur applique le théorème, alors si bien connu, de Barrow que nous avons mentionné dans la note 8 de la Lettre No. 2721. D'après ce théorème il suffit, pour carrer la courbe CHA, de trouver l'équation de la courbe CORF dont la sousnormale NG soit égale à l'ordonnée NH, puisque alors l'aire CHN est égale à ½ ON2. En notation moderne l'auteur a donc réduit de cette manière le problème à l'intégration de l'équation différentielle
de la courbe, rapportée aux axes AC et AR, où AN=z, NH=t, l'auteur applique le théorème, alors si bien connu, de Barrow que nous avons mentionné dans la note 8 de la Lettre No. 2721. D'après ce théorème il suffit, pour carrer la courbe CHA, de trouver l'équation de la courbe CORF dont la sousnormale NG soit égale à l'ordonnée NH, puisque alors l'aire CHN est égale à ½ ON2. En notation moderne l'auteur a donc réduit de cette manière le problème à l'intégration de l'équation différentielle 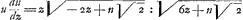 , où u représente ON.
, où u représente ON.
Pour parvenir à cette intégration il emploie une méthode appelée ‘Methodus Craigii’ par Huygens (voir la note 7 de la présente pièce), qui consiste à poser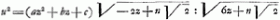 , laissant indéterminés les coëfficients a, b, c, sauf à calculer ensuite les valeurs qu'on doit leur donner pour obtenir l'expression prescrite de la sousnormale. A cet effet l'auteur détermine d'abord la soustangente NP par la règle de de Sluse (voir la note 5 de la présente pièce) dont l'application exige la réduction préalable de l'équation de la courbe à sa forme rationnelle. Après l'achèvement de ces calculs l'expression obtenue pour NP est égalée à celle qu'on obtient par la division de
, laissant indéterminés les coëfficients a, b, c, sauf à calculer ensuite les valeurs qu'on doit leur donner pour obtenir l'expression prescrite de la sousnormale. A cet effet l'auteur détermine d'abord la soustangente NP par la règle de de Sluse (voir la note 5 de la présente pièce) dont l'application exige la réduction préalable de l'équation de la courbe à sa forme rationnelle. Après l'achèvement de ces calculs l'expression obtenue pour NP est égalée à celle qu'on obtient par la division de 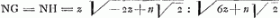 sur ON2=u2. Substituant ensuite dans cette égalité la valeur supposée de u2 on trouve, par la comparaison des coefficients des puissances de z, qu'elle se réduit à une identité, pourvu qu'on suppose: a=-1, b=⅓ n√2, c=⅙n2; mais alors on a:aire
sur ON2=u2. Substituant ensuite dans cette égalité la valeur supposée de u2 on trouve, par la comparaison des coefficients des puissances de z, qu'elle se réduit à une identité, pourvu qu'on suppose: a=-1, b=⅓ n√2, c=⅙n2; mais alors on a:aire 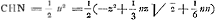 ; donc, pour z=0, CHA=1/12n2, et
; donc, pour z=0, CHA=1/12n2, et 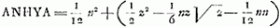 . Retranchant de cette dernière expression l'aire ½ zt du ∆ ANH on trouve le segment
. Retranchant de cette dernière expression l'aire ½ zt du ∆ ANH on trouve le segment
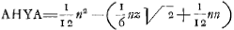 . Enfin, remplaçant z par
. Enfin, remplaçant z par 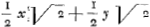 et t par
et t par 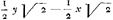 , l'auteur arrive, après quelques réductions fondées sur l'emploi de l'égalité n=(x3+y3):xy, aux formules AHYA=⅙nx2:y, ABZA=⅙ny2:x, qu'on retrouve dans la pièce No. 2793 au bas de la page 417.
, l'auteur arrive, après quelques réductions fondées sur l'emploi de l'égalité n=(x3+y3):xy, aux formules AHYA=⅙nx2:y, ABZA=⅙ny2:x, qu'on retrouve dans la pièce No. 2793 au bas de la page 417.
- voetnoot2)
- Chr. Hugenii etc. Exercitationes Mathematicae, Fasc. II, p. 184.
- voetnoot3)
- A l'exemple d'Uylenbroek nous avons changé en t2, z2, a2 etc. les notations tt, zz, aa etc. du manuscrit.
- voetnoot4)
- La lettre M., ici et dans la suite, remplace le signe de la multiplication.
- voetnoot5)
- On peut consulter, sur cette règle de de Sluse, l'article cité dans la note 1 de la Lettre No. 1924. Ajoutons toutefois qu'elle ne diffère pas essentiellement de celle de Huygens expliquée dans la Lettre No. 1101 et publiée dans l'ouvrage cité dans la Lettre No. 1912, note 7.
- einda)
- Method. Craigii [Christiaan Huygens]Ga naar voetnoot7).
- voetnoot7)
- On rencontre cette méthode de Craig, sous la forme précise dans laquelle elle a été appliquée ici, pour la première fois dans le ‘Tractatus Mathematicus’ de 1693, ouvrage mentionné dans la note 5 de la Lettre No. 2748. Pour le montrer il suffira de citer le passage suivant emprunté à l'Exemplum 1, page 4 de cet ouvrage, où on lit, en adaptant les notations à celles de la figure et du texte de la
présente pièce: ‘Invenienda sit Quadratura Figurae CNH cujus Natura exprimitur hac aequatione.....: Ut habeatur hujus Figurae Quadratura, invenienda est alia Curva COR in qua intercepta NG sit ....; ideo juxta Regulam....praescriptam, multiplicandus est valor datus lineae NG (seu NH) per v, unde productum erit : Jam quia maxima dignitas extra vinculum est v2, ideo apponendi sunt omnes termini inferiores scil. v2, v1, vo (=1) ipso semper maximo termino incluso, qui coefficientibus incognitis affecti aequari debent Quadrato quantitatis u [=ON], unde aequatio quaesitam eminenter continens erit . Ex hac aequatione investigetur valor Analyticus Lineae NG per Leibnitii Methodum hoc modo’; après quoi Craig égale la valeur de NG, obtenue par la méthode de Leibniz, à celle de , pour calculer ensuite les coefficients indéterminés de la manière indiquée dans la note 1 de la présente pièce.
On remarquera l'analogie de cette méthode, qui peut être considérée comme une extension au cas des expressions irrationnelles de celle employée par Craig dans l'ouvrage de 1685, cité dans la note 3 de la Lettre No. 2725, avec le ‘compendium’, décrit dans la note 3 de la No. 2738, dont Huygens se servit en 1692.
D'ailleurs déjà dans l'article ‘Additio ad Methodum Figurarum Quadraturas Determinandi’, qui parut dans les Philosophical Transactions, No. 183, pour les mois juillet-septembre 1686, Craig avait exposé une méthode analogue, laquelle, appliquée par lui au même ‘Exemplum’, consistait à poser a2u4=na6+ma5v+la4v2+ha3v3+ka2v4+gav5+fv6, dans la prévision que l'expression rationnelle pour u4 en v devrait être du sixième degré.
- voetnoot5)
- On peut consulter, sur cette règle de de Sluse, l'article cité dans la note 1 de la Lettre No. 1924. Ajoutons toutefois qu'elle ne diffère pas essentiellement de celle de Huygens expliquée dans la Lettre No. 1101 et publiée dans l'ouvrage cité dans la Lettre No. 1912, note 7.
- voetnoot6)
- Lisez: 2.