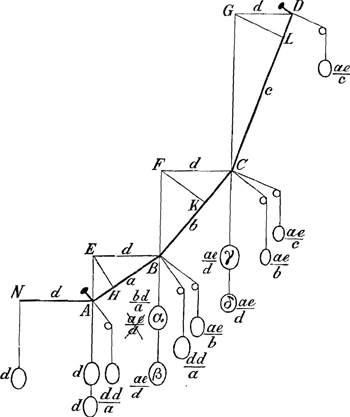
Sint NABCDGa naar voetnoot2) in parabola. Ventus vero secundum axem ejus hoc est parallelè ad EA, FB, GC impellat rectas NA, AB, BC, CD. dico mansuras eo quo sunt positu.
Manebunt enim si, inflante sic vento, nodi C, B, A, ita impellantur ac si ab aequalibus ponderibus rectà deorsum traherentur, quia hoc scimus in parabola dispositis nodis proprium esseGa naar voetnoot3).
Ita vero impelluntur. nam vires quibus a vento premuntur singulae DC, CB, BA, AN, sunt ejusmodi, ac si singulae secundum sibi normales premantur viribus quae sint ut rectae DL, CK, BH, AN. quia vis venti in DG ad vim qua premit DC secundum sibi normalem, hoc est parallelam GL, est ut GC ad GL, ita enim sunt celeritates particularum aeris in ipsas DG, DC agentes, suntque in utramque aequali numero incidentes. ut autem GC ad GL ita GD ad DL.
Itaque si GD referat vim venti in ipsam GD, referat DL vim venti in DC qua
| |
normaliter impellitur. Eodemque modo vires venti in CB, BA, NA, normaliter interpellentis referent rectae CK, BH, AN, quae ultima horizonti parallela poniturGa naar voetnoot4). |
-
voetnoot1)
- Cet Appendice est emprunté à la page 120 du Livre J. On y trouve une figure aualogue à la ‘petite figure’, dont il estquestion dans la Lettre No. 2859, à la page 622, et les calculs et considérations qui ont mené Huygens à la conclusion erronée que la voilière des Bernoulli serait une parabole. Sans doute Huygens, après avoir tracé la figure, a débuté par les calculs que nous avons reproduits à côté d'elle; ensuite ayant acquis, en conséquence de ces calculs, la conviction que les forces verticales qui, appliquées aux noeuds A, B, C, D des interstices AB, BC, CD à projections horizontales égales, pourraient remplacer la pression du vent sur ces interstices, que ces forces, disons nous, devraient être égales entre elles, il en a conclu, profitant d'un théorème qui lui était connu depuis longtemps, que la véritable courbe de la voile était la parabole. Alors il a commencé une démonstration en règle de ce résultat. C'est cette démonstration, d'ailleurs inachevée, qui constitue le texte de cet Appendice et que l'on fera bien de lire avant de s'occuper des calculs mentionnés, qui se trouvent à côté de la figure et sur lesquels nous reviendrons dans la dernière note de cette pièce.
-
voetnoot2)
- On remarquera que les projections horizontales NA, EB, FC, GD des interstices NA, AB, BC, CD sont supposées égales entre elles et à la ligne d.
-
voetnoot3)
- Voir, sur ce theorème, la Propositio 12 de la pièce No. 21.
-
voetnoot4)
- Voici maintenant comment nous croyons que Huygens, d'après les calculs inscrits à côté de la figure, est arrivé à la conclusion erronée, dont tout dépend, que la pression du vent sur les interstices est équivalente à une suite de forces verticales, égales entre elles, appliquées aux noeuds.
Pour commencer il savait donc que, d'après les principes admis par lui et par les Bernoulli, les pressions respectives perpendiculaires aux interstices devaient être proportionnelles aux lignes NA, HB, KC, LD, c'est-à-dire, en posant NA=d, AB=a, BC=b, CD=c, aux expressions d, dd/a, dd/b, dd/c. Remplaçant alors la pression sur l'interstice AB par les deux poids dd/a, appliqués aux noeuds A et B, qui tirent selon la direction perpendiculaire à l'interstice AB et qu'on retrouve facilement dans la figure, il s'ensui vait que les forces analogues, à appliquer aux noeuds des interstices BC et CD, pouvaient, en posant dd/a=e, être représentées par les quatre poids ae/b et ae/c de la figure. (Comparez la première partie des calculs à côté de la figure).
Or, dès ce moment, il ne s'agissait plus que de remplacer ces forces par d'autres appliquées aux mèmes noeuds, mais tirant dans le sens vertical. Pour y réussir Huygens part du principe qu'il a déjà appliqué dans la pièce No. 2835, et d'aprèslequel des systèmes de forces équivalentes doivent accomplir le même travail pour tout déplacement virtuel compatible avec les liaisons.
Sans doute, puisque les clous qui figurent aux points A et D le prouvent, Huygens a alors considéré le mouvement virtuel bien défini qui reste possible après la fixation des noeuds A et D et il a commencé par calculer, dans cette supposition, la force verticale α capable de remplacer la force dd/a, ou e, tirant le noeud B. Pour cette force α il trouve facilement (voir la seconde partie des calculs mentionnés) l'expression ae/d=α, et il procède ensuite au calcul du poids β qui doit remplacer le poids ae/b tirant le même noeud B dans la direction perpendiculaire à l'interstice BC. Mais alors, dans un moment d'inadvertance, au lieu de recourir au même mouvement virtuel qui avait fourni l'expression pour α, comme cela était absolument nécessaire pour rester dans la vérité, il emploie pour ce nouveau calcul le mouvement virtuel qu'on obtient en fixant le noeud C. En effet il est clair que cette supposition devait mener à l'expression ae/d=β que l'on trouve dans le calcul à côté de la figure.
De même, le poids γ, destiné à remplacerla force ae/b qui tire le noeud C, est calculé dans la supposition que le noeud B a été fixé, et le poids δ dans celle de la fixation du noeud D. Trouvant de cette manière α=β=γ=δ=ae/d, donc α+β=γ+δ, Huygens en conclut à l'égalité de toutes les forces verticales, destinées à remplacer les pressions du vent sur les interstices sans intervenir dans l'équilibre de la chaîne formée par eux.
Remarquons encore que plus tard, comme nous l'avons reproduit dans la figure, Huygens a biffé l'expression ae/d, écrite d'abord à côté du poids α, et l'a remplacé par bd/a; mais cette correction est le résultat d'un nouveau malentendu, puisqu'on ne peut obtenir cette valeur qu'en supposant que la force dd/a, qui doit être remplacée par α, soit perpendiculaire sur BC (et non sur AB comme elle l'est en réalité) et que c'est le noeud C qui a été fixé.
Ajoutons que la pièce No. 2835, où le même principe est appliqué en toute rigueur, nous prouve, si cela était nécessaire, que la bévue commise ici par Huygens, n'est qu'accidentelle, étant la conséquence d'une première pensée sur laquelle il est revenu d'ailleurs, comme il résulte de la phrase ajoutée en marge de la Lettre No. 2859 et reproduite dans la note 9 de cette pièce.
|