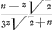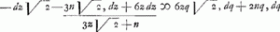No 2862.
[B. de Volder] à Christiaan Huygens.
[1694].
Appendice IIIGa naar voetnoot1) au No. 2859.
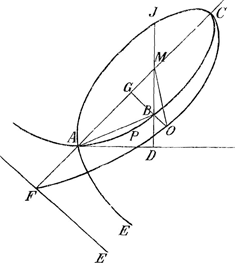
Sit AD ∞ x DB ∞ y AG ∞ z GB ∞ t et x3+y3 ∞ nxy
erit z√2 ∞ x+ y t√2 ∞ x- y t ∞ z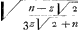 .
Sit curva COF, talis, ut ducta ex M recta ad punctum O, in quo GB secat curvam COF, sit in curvam normalis, posita GO= v, ponatur pro illa curva azz+ bz+ c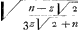 ∞ vvGa naar voetnoot2)
Ex qua aequatione ut inveniatur GM, secundum methodum Leibn. Ga naar voetnoot3) fiat azz+ bz+ c ∞ p et 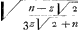 ∞ q, erit Ga naar einda) 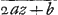 , dzGa naar voetnoot4) ∞ ∞ dp et 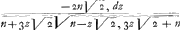 ∞ dqGa naar voetnoot5) et pdq+ qdp ∞ 2 vdv, sive
| |
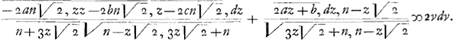
adeoque dz ad dv ut 2 v ad -2 an√2, zz etc., sive OG ad GM.
Erit itaque GM=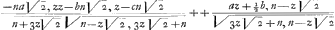 ∞ z ∞ z 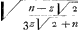 |
adeoque -6az3-3bzz+annz+½bnn ∞-6z3+2nzz√2+nnz+na√2,-cn√2
Unde a ∞ 1 b ∞-⅓ n√2 c ∞-⅙ nn. adeoque cum z√2 nequeat esse major, quam nGa naar voetnoot6), erit mutatis signis Ga naar voetnoot7) - zz+⅓ n√2, z,+⅙ nn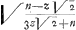 ∞ vv sive+ 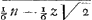 , in 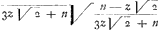 ∞ vv. Hinc si v ∞ 0, ponatur, erit z ∞ n√½, aut z ∞-⅓ n√2. Ex quo patet curvam COF rectam CF secturam in punctis C et F. Hinc erit spatium GCB ∞-½ zz+⅙ n√2, z+
| |
+1/12 nn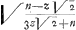 Ga naar voetnoot8) Ga naar voetnoot8) et posito z ∞ o, erit spatium ABC, ut et AFE ∞ ∞ 1/12 nn, et ABG ∞ 1/12 nn+ 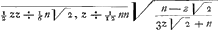 , demtoque triangulo ABG ∞ ½ tz, ∞ ½ zz 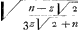 erit spatium ABP ∞ ∞ 1/12 nn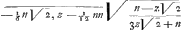 Est autem 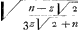 ∞ ∞ t/ z ∞ x- y/ x+ y Hinc ABP ∞ 1/12 nn, 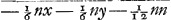 , x- y/ x+ y
| ABP ∞ ⅙nny-⅙nxx+⅙nyy/x+y ∞ nnyx-nx3+ny2x/6x, x+y. |
| Est autem nyx ∞ x3+y3 Hinc ABP ∞ ny3+nyyx/6x, x+y ∞ nyy/6xGa naar voetnoot9). |
Nec dissimili ritu res se habet in caeteris casibus. |
-
voetnoot1)
- Cet Appendice, comme celui qui précède, contient une solution du problème de la quadrature du folium de Descartes. Consultez d'ailleurs la note 19 de la Lettre No. 2859.
-
voetnoot2)
- Comme dans la solution précédente, c'est encore ici la méthode de Craig, décrite dans la note 7 de la pièce No. 2861, qui va être appliquée, en combinaison, comme chez Craig luimême, avec le théoreme de Barrow (voir la note 8 de la Lettre No. 2721), d'après lequel on a ici: aire CBG=½ OG2=½ v2, puisque, par construction, la sousnormale GM de la courbe COF égale BG l'ordonnée de la courbe CBPA.
-
voetnoot3)
- Celle publiée par Leibniz dans l'article cité dans la note 5 de la Lettre No. 2205.
-
einda)
- aequ.o diff.lis [Christiaan Huygens].
-
voetnoot4)
- Ici et dans la suite la virgule figure comme signe de multiplication. D'ailleurs la notation employée est un peu singulière et pas toujours conséquente. Toutefois nous n'y avons rien changé, puisqu'en refaisant les calculs on trouvera facilement la vraie signification des formules.
-
voetnoot5)
- Ici on lit encore en marge: ‘Verum hoc esse patet ex seq. calculo:
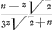 ∞ qq ∞ qq
-dz√2 ∞ 3qq√2, dz+6zq√2, dq+2nq, dq
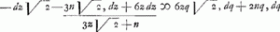
-
voetnoot6)
- Puisque alors l'expression pour t=GB, qui se trouve en tête de cette pièce, deviendrait imaginaire.
-
voetnoot7)
- En effet, sans ce changement de signe l'expression pour vv, qui va suivre, aurait, pour z√2 positif et < n, une valeur toujours négative, puisqu'on a z2-⅓nz√2-⅙n2==⅙(z√2-n)(3z√2+n).
-
voetnoot8)
- D'après le théorème de Barrow; voir la note 2.
-
voetnoot9)
- C'est un des résultats annoncés par Huygens vers la fin de la pièce No. 2793.
|
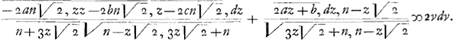
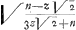 ∞ vv sive+
∞ vv sive+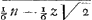 , in
, in 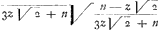 ∞ vv. Hinc si v ∞ 0, ponatur, erit z ∞ n√½, aut z ∞-⅓n√2. Ex quo patet curvam COF rectam CF secturam in punctis C et F. Hinc erit spatium GCB ∞-½zz+⅙n√2, z+
∞ vv. Hinc si v ∞ 0, ponatur, erit z ∞ n√½, aut z ∞-⅓n√2. Ex quo patet curvam COF rectam CF secturam in punctis C et F. Hinc erit spatium GCB ∞-½zz+⅙n√2, z+
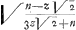 Ga naar voetnoot8) et posito z ∞ o, erit spatium ABC, ut et AFE ∞ ∞ 1/12 nn, et ABG ∞ 1/12 nn+
Ga naar voetnoot8) et posito z ∞ o, erit spatium ABC, ut et AFE ∞ ∞ 1/12 nn, et ABG ∞ 1/12 nn+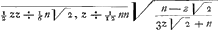 , demtoque triangulo ABG ∞ ½ tz, ∞ ½ zz
, demtoque triangulo ABG ∞ ½ tz, ∞ ½ zz 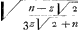 erit spatium ABP ∞ ∞ 1/12nn
erit spatium ABP ∞ ∞ 1/12nn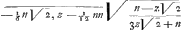 Est autem
Est autem 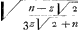 ∞ ∞ t/z ∞ x-y/x+y Hinc ABP ∞ 1/12nn,
∞ ∞ t/z ∞ x-y/x+y Hinc ABP ∞ 1/12nn, 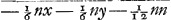 , x-y/x+y
, x-y/x+y



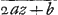 , dz
, dz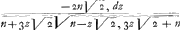 ∞ dq
∞ dq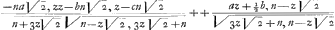 ∞ z
∞ z