Oeuvres complètes. Tome IV. Correspondance 1662-1663

N^o 1146.
R.F. de Sluse à [Christiaan Huygens].
[août 1663].

La lettre se trouve à Leiden, coll. Huygens.

Nobilissime Domine

Apologiam Timauri Antiatis, seu potius Clarissimi Caroli Datj, prioribus meis¹⁾ non adiunxeram, quod an illam Florentia accepisses, a te certior fieri expectarem,

1) Consultez la Lettre N^o. 1137.

[p. 398]

et non magni referre arbitrarer hanc modicj temporis moram, cum te Hagae-Comitis esse mihi persuaderem.

Sed aliquot postquam ad te scripseram diebus, transijt hac Nobilis Vir Dominus Monconisius²⁾, qui et Parisijs nuper fuisse, et nunc Londinj agere te mihi retulit; multaque adiunxit de praeclaris virorum literatorum conatibus, qui Scientiam Naturalem experimentis stabilire contendunt. Anceps itaque eram an meas accepisses, cum me sollicitudine liberarunt literae tuae datae 3a huius³⁾, quibus lectis, continuo mittendam censui Apologiam eadem viâ quà priores acceperas. De Celeberrimi Pascalij obitu⁴⁾ certiorem me reddidit idem Monconisius, non sine magno animj mej moerore, qui viri doctrinam et humanitatem maximj faciebam. Sed, vt ait ille, ad hoc sacramentum adacti sumus fere mortalia, ϰαὶ τῇ ἀνάγϰῃ συγχωρεῖν. Non ingratum tibi futurum arbitror si adiungam id quod nuper ad me Florentia scriptum est, primam nempe experimentorum physicorum in Academiâ Serenissimi Principis factorum, partem⁵⁾, iam editioni paratam: Eximium Borellum⁶⁾ breui daturum in lucem librum Physicomathematicum de motu animalium⁷⁾; Rinaldinum⁸⁾ vero artem Analyticam⁹⁾: alium denique, opusculum de Aquarum fluxu¹⁰⁾, quibus scientiarum pomaeria promouenda confido. Nuper etiam Patavio scripsit ad me Pater Stephanus Angeli¹¹⁾ Mathematum illic Professor et celebris Caualerij discipulus, se hac aestate Libellum Geometricum edidisse in quo Spatiorum Spiralium mensuras¹²⁾

2) Sur Balthasar de Monconys, voir la Lettre N^o. 765, note 8.

3) Cette lettre de Chr. Huygens à de Sluse, du 3 août 1663, ne s'est pas trouvée dans nos collections.

4) Blaise Pascal était mort déjà le 19 août 1662.

5) Sur cet ouvrage ‘Saggi di Naturali Experienze. 1667,’ voir la Lettre N^o. 1000, note 5.

6) Sur Giovanni Alsonso Borelli, voir la Lettre N^o. 536, note 4.

7) On en trouve la réimpression:
Joh. Alphonsi Borelli Neapolitani Matheseos Professoris, De Motu Animalium, Pars Prima [et secunda] Editio Nova, a plurimis mendis repurgata, ac Dissertationibus Physico-Mechanicis de Motu Musculorum, et de Effervescentia, et Fermentatione, Clarissimi Viri Joh. Bernoullii Matheseos Professoris Basileensis, aucta, & ornata. Hagae Comitum, Apud Petrum Gosse. mdccxliii. II Vol. in-4^o.

8) Sur Carlo Renaldini, voir la Lettre N^o. 697, note 10.

9) Ars Analytica Mathematum. Authore C. Renaldino. Tomus I, Florentiae 1665. in-4^o.
Les Tomes II et III parurent ‘Pataviae’ 1669 et 1668. in-4^o.

10) Nous n'avons pas réussi à découvrir cet ouvrage, ni son auteur.

11) Sur Stefano degli Angeli, voir la Lettre N^o. 732, note 14.

12) Voir l'ouvrage cité dans la Lettre N^o. 938, note 6.

[p. 399]

ostendit, et Clarissimi Vallisij errores¹³⁾ notat. Res hoc schemate explicari potest.



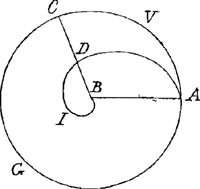Jntelligatur centro B circulus AVCG, in quo descripta Spiralis ADB, et quilibet radius secans spiralem, BDC. Nunc si spiralis ita composita intelligatur, vt sit eadem ratio CB, ad DB, quae est circumferentiae ACGA, ad arcum CGA, spiralis erit Archimedis.

Sin autem retentâ eadem ratione CB ad DB, intelligatur ita esse quaelibet dignitas circumferentiae ACGA, ad homogeneam arcus CGA, tunc producentur illae insinitae spirales quas Pater Stephanus examinat, et asserit spatium spirale ABIDA ad circulum, esse in primâ seu Archimedis, vt j ad 3, in secundâ vt j ad 5, in tertiâ vt j ad 7 et sic in infinitum in ratione vnitatis ad numeros impares. Vallisius vero (si eum recte intellexit) pronunciat primum spatium esse ad circulum vt j ad 3, secundum vt j ad 4, et sic semper in ratione vnitatis ad numeros ternarium sequentes. Cum vtriusque Auctoris librj non essent ad manum, rem ad calculos reuocauj, sed generalius; considerando nempe spirales ita componj, vt eadem sit ratio cuiuslibet dignitatis CB, ad homogeneam DB, quae est cuiuslibet dignitatis circumserentiae ACGA, ad homogeneam arcus CGA: et regulam facilem invenj quâ totum negotium absoluitur. Est enim semper vt exponens dignitatis quae consideratur in radio et eius partibus, ad eundem exponentem, vna cum duplo exponentis dignitatis quae consideratur in circumferentiâ et eius partibus, ita totum spirale ad circulum, cuius assertionis veritatem....¹⁴⁾

13) Consultez l'ouvrage de J. Wallis ‘de Cycloide Tractatus II.’ Voir la Lettre N^o. 690.

14) Le reste de la lettre en a été arraché.