Oeuvres complètes. Tome IV. Correspondance 1662-1663

N^o 990.
P. de Fermat à [M. Cuzeau de la Chambre^a)].
[1 janvier] 1662.
Appendice I au N^o. 989¹⁾.

Une copie se trouve à Leiden, coll. Huygens.
La lettre a été publiée par Clerselier dans les ‘Lettres de Monsieur des Cartes.’

A Toulon de l'an 1662.

Monsieur

Il est juste de vous obeir & de terminer en sin par vostre entremise le vieux demeslé qui a esté depuis si long temps entre Monsieur Des Cartes & moy sur le suject de la refraction et peutestre seray je assez heureux pour vous proposer une paix que vous trouverez auantageuse à tous les deux partis.

Je vous ay dit autrefois dans ma premiere Lettre que Monsieur Des Cartes n'a jamais demonstré son principe; car qu'outre que les comparaisons ne seruent guere à fonder des demonstrations il employe la sienne a contresens et suppose mesme que le passage de la lumiere est plus aysé par les corps durs que par les rares, ce qui est apparemment faux. Je ne vous dis rien du defaut de la demonstration en elle-

a) ℞ de mon frere Louis, qui l'avoit de Monsieur Petit⁸⁾ a qui elle est escrite par Monsieur de Fermat. [Chr. Huygens.]

8) Chr. Huygens ignorait que cette lettre ne sut pas adressée directement à P. Petit.

1) De ces trois Appendices N^os. 990, 991, 992, la copie qui se trouve à Leiden n'est pas de la main de Lodewijk Huygens, comme il suivrait de la Lettre N^o. 988, mais de celle de de Carcavy, qui a sauté quelques mots; dans notre texte nous avons suivi la copie de la Bibliothèque Nationale à Paris, qui est plus exacte que celle de Leiden.

[p. 76]

mesme, quand bien la comparaison dont il se sert seroit bonne et admissible en ceste matiere, pour ce que j'ay traitté tout cela bien au long dans mes lettres²⁾ à Monsieur Des Cartes pendant sa uie, ou dans celles que j'ay escrit à Monsieur Clairsillier³⁾ depuis sa mort. J'adjouste seulement qu'ayant veu le mesme principe de Monsieur Des Cartes dans plusieurs autheurs qui ont escrit apres luy, leurs demonstrations non plus ne me paraissent point recevables et ne meritent point de porter ce nom. Herigone⁴⁾ se sert pour le demonstrer des equiponderans et de la raison des poids sur les plans inclinez. le Pere Maignan⁵⁾ y veut parvenir d'une autre maniere; mais il est aysé de voir qu'ils ne demonstrent ni l'un ni l'autre, et qu'apres auoir leu et examiné auec soin leur demonstrations, nous sommes aussi incertain de la verité des principes qu'apres auoir leu Monsieur Des Cartes.

Pour sortir de cet embaras et tascher de decouvrir la veritable raison de la refraction je vous indiquay dans ma lettre que si nous voulions employer dans ceste recherche ce principe si commun & si estably que la nature agit tousjours par les voyes les plus courtes, nous pourrions y trouver facilement nostre compte, mais parce que vous doutastes d'abord que la nature en conduisant la lumiere par les deux costez d'un triangle puisse jamais agir par une voye aussi courte que si elle la conduisoit par la base ou par la soustendante, Je m'en vay vous faire voir le contraire de vostre sentiment ou plustost de vostre doutte par un exemple aisé. Soit en la figure à part, le cercle ACBG, duquel le diametre soit AOB, le centre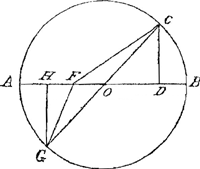



O, et un autre diametre COG. des points C. & G. soyent tirez les perpendiculaires sur le premier diametre GH. DC. Supposons que le premier diametre AOB separe deux milieux differens, dont l'un qui est celuy de dessoubs AGB, soit le plus dense et celuy de dessus ACB soit le plus rare, en telle sorte par exemple que le passage par le plus rare soit plus aysé que par le plus dense en raison double. Il suit de cette supposition que le temps qu'employe le mobile ou la lumiere de C en O est moindre que celuy qui les conduit de O en G. Et que le temps du mouvement de C en O. qui se fait dans le milieu le plus rare, n'est que la moitié du temps du mouvement de O en G. Et par consequent la mesure

2) Voir dans les ‘Lettres de Monsieur des Cartes,’ Tome III, 1667, les lettres N^os. 37 à 55. La lettre du texte est la 51 me de cette collection.

3) Il s'agit de Claude Clerselier. Voir la Lettre N^o. 732, note 22.

4) Consultez l'ouvrage cité dans la Lettre N^o. 139, note 4.

5) Voir l'ouvrage cité dans la Lettre N^o. 498, note 8.

[p. 77]

du mouvement entier par les deux droittes CO & OG. peut estre representee par la somme de la moitié de CO et de la totale OG. de mesme si vous prenez un autre point comme F. le temps du mouuement par les deux droittes CF et FG. peut estre representé par la somme de la moitié de CF et de la totale FG. Supposons maintenant que le rayon CO. soit 10. et par consequent le diametre total COG. sera 20. que la droitte HO. soit 8. la droitte OD. soit aussi 8. et qu'enfin la droitte OF. ne soit que 1. Je dis qu'en ce cas le mouvement qui se fait par la droitte COG. se fera en un temps plus long que celuy qui se fait par les deux costez du triangle CF. FG. Car si nous prouvons que la moitié de CO. jointe à la totale OG. contient plus que la moitie de CF. jointe à la totalle FG. la conclusion sera manifeste puisque ces deux sommes font justement la mesure de ces deux mouvemens, or la somme de la moitie de CO. et de la totale OG. fait justement 15. Et il est evident par la construction que la droitte CF. est esgalle à la racine quarrée de 117. Et que la droitte FG. est esgalle à la racine quarree de 85. Mais la moitie de la premiere racine jointe à la seconde fait moins que 59/4. et 59/4 sont encore moindres que 15. donc la somme de la moitié de CF. et de la totalle FG, est moindre que la somme de la moitié de CO. et de la totale OG. et partant le mouvement par les deux droittes CF. FG. se fait en moins de temps que par la base ou soustendante COG.

Je suis venu jusques lá sans beaucoup de peine mais il a fallu porter la recherche plus loin, et parce que pour satisfaire à mon principe il ne suffit pas d'auoir trouvé un point comme F. par ou le mouvement naturel se fait plus viste, plus aisement et en moins de temps que par la droitte COG. mais il faut encor trouver le point qui fait la conduite en moins de temps que quelqu'autre que ce soit pris des deux costez, il m'a esté necessaire auoir recours en ceste occasion à ma methode de maximis et minimis⁶⁾ qui expedie ceste sorte de questions auec assez de succez.

Des que j'ay voulu entreprendre ceste analyse j'ay eu deux obstacles à surmonter, le premier que bien que je fusse asseuré de la verité de mon principe, et qu'il n'y ayt rien de si probable ni de si apparent que ceste supposition, que la nature agist tousiours par les moyens les plus aysez, c'est à dire ou par les lignes les plus courtes lors qu'elles n'emportent pas plus de temps, ou en tout cas par le temps le plus court afin d'accourcir son trauail & de venir plustost à bout de son operation (ce que le precedent calcul confirme dautant plus qu'il paroist que la lumiere a plus de difficulté à traverser les milieux denses que les rares puisque vous voyez que la refraction vise vers la perpendiculaire dans mon exemple ainsi que l'experience le confirme, ce qui pourtant est contraire à la suppositionde Monsieur Des Cartes;) neantmoins j'ay esté adverty de tous costez et principalement par

6) Voir dans la collection (décrite dans la Lettre N^o. 221, note 1) le mémoire:
Methodus ad disquirendam maximam & minimam.

[p. 78]

Monsieur Petit que i'estime infiniment, que les experiences s'accordent exactement auec la proportion que Monsieur Des Cartes a donné aux refractions et que bien que sa demonstration soit fautive il est à craindre que je tenteray inutilement d'introduire une proportion differente de la sienne et que les experiences qui se feront apres que j'auray publié mon invention la pourront detruire sur l'heure. Le second obstacle qui s'est opposé à ma recherche a esté la longueur et la difficulté du calcul, qui dans la resolution du probleme dont je vous parlay dans ma lettre, et que je vous temoignois n'estre pas des plus aysez, presente d'abord 4 lignes par leur racine quarrées et engage par consequent en des asymmetries qui aboutissent à une tresgrande longueur.

Je me suis defait du premier obstacle par la connoissance que j'ay qu'il y a infinies propositions differentes de la veritable qui approche d'elle si insensiblement qu' elles peuuent tromper les plus habiles et les plus exactes observateurs. Ainsi n'y ayant que le second obstacle à vaincre, je m'estois resolu tres souvent d'employer la bien-aymée Geometrie (C'est ainsi que Plutarque l'appelle) pour uous satisfaire et pour me satisfaire moy-mesme; mais l'apprehension de trouver apres une longue et penible operation quelque proportion irreguliere et fantasque et la pente naturelle que j'ay vers la paresse ont laissé la chose en cet estat jusqu'à la derniere semonce que Monsieur le President de Miremont vient de me faire de vostre part, que je prens pour une loy plus forte que ni mon apprehension ni ma paresse, si bien que je me suis resolu de vous obeïr sans autre retardement.

J'ay donc procedé sans remise en vertu de l'obedience, comme parlent les moines, à l'execution de vos ordres; et j'ay fait l'entiere analyse en forme dans la quelle le desir passioné que j'ay eu pour vous satisfaire m'a inspiré une route qui a abregé la moitié de mon travail, et qui a reduit les quatre asijmmetries que i'avois eu en veue la premiere fois à deux seulement, ce qui m'a notablement soulagé.

Mais le prix de mon travail a esté le plus extraordinaire, le plus impreveu et le plus heureux qui fut jamais, car apres avoir couru par toutes les equations, multiplications, antitheses et autres operations de ma methode, et avoir enfin conclu le probleme que vous verrez dans un feuillet separé⁷⁾, j'ay trouvé que mon principe donnoit justement & precisement la mesme proportion de refraction que Monsieur Descartes à establie.

J'ay esté si surpris d'un evenement si peu attendu, que j'ay peine à revenir de mon estonnement; j'ay reïteré mes operations Algebriques diverses fois et tousjours le succes a esté le mesme, quoy que ma demonstration suppose que le passage de la lumiere par les corps denses soit plus malaysé que par les rares ce que voy tres-vray et indisputable, et que neantmoins Monsieur Des Cartes suppose le contraire.

7) Consultez l'Appendice N^o. 992.

[p. 79]

Que devons nous conclure de tout cecy? ne suffira-il pas, Monsieur, aux Amis de Monsieur Des Cartes que je luy laisse la possession libre de son theoreme? N'aura-t'il pas assez de gloire d'auoir connu les demarches de la nature dans la premiere veuë et sans l'ayde de la demonstration? Je luy cede donc la victoire et le champ de bataille, et je me contente que Monsieur Clairsiller me laisse entrer du moins en la societé de la preuve de ceste verité si importante, & qui doibt produire des consequences si admirables.

J'adjouste mesme en faveur de son amy qu'il semble que ceste grande verité naturelle n'a pas osé tenir devant ce grand genie, & qu'elle s'est rendue & decouverte à luy sans s'y laisser forcer par la demonstration, à l'exemple de ces places qui quoy que bonnes d'ailleurs et de difficile prise ne laissent pas sur la seule reputation de celuy qui les attaque, de se rendre sans attendre le canon.

Je vous annonce donc, Monsieur, j'annonce à Monsieur Clairsiller et à tous les amis de Monsieur Des Cartes qu'il ne tiendra plus à l'incredulité des Geometres qu'on ne doiue attendre les merueilles que Monsieur Des Cartes a fait esperer auec raison de ses lunettes elliptiques et hyperboliques, pourveu qu'on puisse trouver des ouvriers assez habiles pour les faire et pour les adjuster.

Il resteroit encore vne petite difficulté que la comparaison de Monsieur Des Cartes seulle produit, c'est qu'il ne paroist pas encore pourquoy la balle qui est poussee dans l'eau n'approche pas de la perpendiculaire, ainsi que la lumiere, mais outre qu'on pourroit soubçonner que la reflexion se mesle dans cet exemple à la refraction et que la figure ou la grauité peuuent contribuer à la difference de ce mouuement, je n'ay garde d'entrer dans une matiere purement Physique. Ce seroit entreprendre sur vous, Monsieur, qui en estes le Maistre & faire irruption dans vostre domaine. Je finis donc, apres vous auoir declaré que je consens si vous le trouvez à propos, que l'accommodement entre les Cartesiens & moy soit publié dans les Academies, et apres vous auoir conjuré de recevoir au moins l'effet de ma prompte obeissance pour une preuve certaine et plus que demonstrative auec laquelle ie suis,

Monsieur,

Vostre tres-humble & tres-obeissant serviteur Fermat.

8) Chr. Huygens ignorait que cette lettre ne sut pas adressée directement à P. Petit.