Oeuvres complètes. Tome I. Correspondance 1638-1656

N^o 139.
Christiaan Huygens à A. Tacquet.
10¹⁾ décembre 1652.

La minute et la copie se trouvent à Leiden, coll. Huygens.
La lettre est la réponse au No. 137. Tacquet y répondit par le No. 141.

Patri Tacquet.

Coeperam jam persuadere mihi non pervenisse ad te literas meas Vir Clarissime, sed casu aliquo intercidisse, cum ecce responsum inopinanti allatum est, atque insigni me hilaritate erexit. Maximas sane ex mediocri mora usuras persolvisti, quantasque mihi debitas non fuisse agnosco etiamsi in hoc genere avarissimus. Cum autem et te quantum ad haec attinet similiter ut ego affectum credam non verebor ne prolixitatem meam culpes, si ad nonnulla capita epistolae tuae verbosius respondero. Ante omnia vero gratiam habeo quod luculenter adeo de inventione mea circa Hyperboles quadraturam te sentire significasti, siquidem ex mera benevolentia id procedere judico quod primi industriae meae partus tam pulchri tibi videntur atque extolluntur longe supra meritum. Porro perlubenter vidi argumentationem meam contra conatus Cyclometricos Patris Gregorij ratiocinio tuo adjutam, quaesivi in exetasi mea qua potissimum ratione ad absurdum illum deducerem. Tu vero erroris originem prorsus tangis cum propositiones 39 et 12 erroris convincis; quas ego quoque mendosas inveneram. sed in obscuris facilius et confidentius contradicturum arbitra-

1) Dans la minute il semble qu'il y ait ‘16,’ mais les Adversaria de Christiaan Huygens indiquent qu'il écrivit cette lettre le ‘10’. Cette date s'accorde mieux avec celle de la réponse de Tacquet, écrite le 18 décembre.

[p. 202]

bar. Verum de his superfluum arbitror pluribus disserere, cum de summa rei inter nos conveniat. Itaque ad thesin tuam transeo, quam et tuis et aliorum exemplis stabilire videris. Sane cum antea sensum ejus verum ignorarem, nunc plane quid statuas percipio neque tamen assentiri tibi possum. Patieris autem ut confido non illibenter Vir Clarissime redintegrari tibi disputationem qua proculdubio jam pridem multa cum laude defunctus es. Mihi igitur videtur demonstratio quam proposuisti, non directa esse sed ex earum genere quae ad absurdum deducunt, quod autem absurdi mentione caret, eo imperfectam manere. Etenim post conclusionem tuam, quae est, Ergo tota BG major est duabus BC, CH, haec addenda dicerem, sed eadem BG duabus BC, CH non major esse ponebatur, Ergo simul et major erit, et non major, quod est absurdum. Quare falsum erit illud unde hoc consequitur. ac proinde BG major duabus BC, CH. Ita video Euclidem fecisse in propositione 12 libri 9 à te allegata, item Archimedem in propositionibus 8, 9, et 10 libri de Conoidibus et Sphaeroidibus²⁾. Cardani librum nunquam evolvi, et demonstrationem Theodosii libri 1 Sphaericorum propositionis 12 tantum directam videre contigit, eam scilicet quam Herigonus³⁾ affert⁴⁾. Fortassis autem superfluum tibi videtur ulterius progredi, postquam id quod

2) Archimedis Opera non nvlla a Frederico Commandino Vrbinate nvper in latinvm conversa, et Commentariis illvstrata. Quorum nomina in sequenti pagina leguntur. [Circuli dimensio. De lineis spiralibus. Quadratura paraboles. De conoidibus, & sphaeroidibus. De arenae numero]. Venetiis apud Paulum Manutium. Aldi F. mdlviii. in-folio.

3) Pierre Herigone vivait à Paris en 1634 et 1644; il était maître de mathématiques. Il résulte de sa polémique avec le professeur Johan Baptiste Morin à Paris au sujet du problème des longitudes, qu'il avait été membre de la commission pour juger le livre de Morin. Voyez l'ouvrage de la note suivante, Tomes 4 & 5.

4) Le démonstration se trouve Tome V, page 235 de l'ouvrage suivant:
Cvrsvs mathematicvs Nova, brevi et clara methodo demonstratvs: Per Notas reales & vniversales, citra vsum cuiuscumque idiomatis intellectu facile. Covrs mathematiqve demonstré d'vne nouvelle, briefve, et claire methode. Par Notes reelles & universelles, qui peuuent estre entenduës facilement sans l'vsage d'aucune langue. Par Pierre Herigone, Mathematicien. a Paris. m.dc.xxxiv chez l'Autheur, en l'Isle du Palais, à l'enseigne de l'Anguille & chez Henry le Gras au troisiesme pilier de la grande Salle du Palais. in-8^o.
De même que ce tître, ceux des volumes sont moitié latin, moitié français, nous n'en donnerous que la partie française:
Tome premier dv cours mathematiqve, contenant les XV Liures des Elemens d'Euclide vn appendix de la Geometrie des Plans, les Dates d'Euclide, cinq livres d'Apollonius Pergeus du lieu resolu, la Doctrine de la Section des Angles.
Tome second dv Covrs mathematique, contenant l'Arithmetique practique: le Calcul Ecclesiastique: & l'Algebre, tant vulgaire que specieuse, auec la methode de composer & faire les demonstrations par le retour ou repetition des vestiges de l'Analyse.
Tome troisiesme dv Cours mathematiqve, contenant la construction des Tables des Sinus, Et Logarithmes, auec leur vsage aux interests, & en la mesure des triangles rectilignes: La Geometrie practique: Les Fortifications: la Milice: & les Mechaniques.
Tome quatriesme dv Cours mathematiqve, contenant la Doctrine de la Sphere du Monde: la Geographie tant ancienne que moderne, designée par degrez & minutes des longitudes & latitudes, & l'Art de nauiger. Acheué d'imprimer le 8 de novembre 1634.
Tome cinqviesme dv Cours mathematiqve, contenant l'Optique, la Catoptrique, la Dioptrique, la Perspectiue, la Trigonometrie des Spheriques, la Theorie des Planetes, tant selon l'hypothese de la terre immobile, que mobile, la Gnomonique, & la Musique. 8^o. ‘acheué d'imprimer le 14 Aoust 1637.’
Tome sixiesme et dernier, ou supplement du Cours Mathematique, contenant les Effections Geometriques des equations cubiques & affectées. L'Isagoge de l'Algebre. La methode de mettre en Perspectiue toutes sortes d'objets par le moyen du Compas de proportion. La theorie des Planetes, distinguée selon les hypotheses de la terre immobile & mobile. L'Introduction en la Chronologie, avec vne Table des choses plus notables par ordre alphabetique: Et vn Catalogue des meilleurs Autheurs des Mathematiques.
Les tomes II à IV ont paru en mdcxlv.

[p. 203]

verum est directa demonstratione es assecutus nempe quod BG major est duabus BC, CH. Sed omnino inquirendum est, utrum hoc ita se habere recte demonstratum fuerit. Quid enim si quis statuat, quod omnis figura plana rectangulo contenta eique basin et altitudinem eandem habens, sit ejus rectanguli subsesquialtera⁵⁾, atque ex eo demonstret parabolam inscripti maximi trianguli sesquitertiam⁶⁾ esse? Ea quidem et demonstratio et conclusio vera erit, sed tamen fidem non faciet mihi, si aliunde parabolae quadraturam non didicerim. Ratio autem, quare istiusmodi argumentatione non persuadear, ea sola est quod sciam aliquid in praemissis contineri quod falsum est. Sanè in eâ quam afferre tibi visum fuit, non quidem apparet à principio falsum quid poni, sed dubium tamen, quum non constet utrum BG major sit an non major duabus BC, CH. Quomodo igitur omnia, quae inde consequuntur non aequè dubia sint? Itaque plane ita tenendum reor, in directa demonstratione omnia ex quibus argumentatio deducitur certa esse debere; quum autem certa non sunt sed vel dubia vel aperte falsa tum fieri quidem posse ut ad veram conclusionem perveniatur, sed eam utrum vera sit an falsa ex ea demonstratione quatenus directa permanet minime cognosci. Et si bene rem examines, videbis sine dubio tuam ipsius demonstrationem tibi persuadere non posse (si te id ignorare fingas,) quod BG sit major duabus BC, CH; nisi cogitatione saltem clausulam de absurdo adjicias quam paulo ante descripsi. Revera tamen mirandae apparent demonstrationes istiusmodi, et tanto quidem mirabiliores quanto magis ab ipsa falsa seu dubia positione argumentatio procedit. Euclidis demonstratio ad finem usque falsam positionem habet admistam. In Tua verò in principio fortè factum est ut utilis esset ad ostendendum quod BG inaequaliter dividitur in E, cum BE ipsi BC aequalis sumitur. nam hoc etiam alia ratione facile ostendi potuisset, atque ita directa fuisset demonstratio. Archimedes in propositionibus supra adductis, positione sua in demonstrando non utitur, ideoque admirationem non parit, et potuisset aequè commodè de puncto quolibet in ellipsi sumpto, ostendisse quod id in superficie coni esset vel cylindri idque argumentatione directa. Invenio me genere illo usum fuisse cum alia ratione demonstrare non possem.

In triangulo punctum ex quo rectae omnium brevissimae ad tres angulos ducuntur,

5) = 2:3.

6) = 4:3.

[p. 204]

esse illud in quo arcus similes super lateribus intrinsecus descripti se intersecant qui singuli sint tertia pars circumferentiae; ac proinde in triangulo amblygonio angulum obtusum majorem 120 partibus habente punctum ejusmodi non dari sed in ipsum obtusi anguli punctum quodammodo incidere.

Scribis tibi in refractionibus Theorema quoddam investiganti demonstrationem adductam usu venisse, quod ego non sine quodam voluptatis sensu animadverti, te scilicet in ea quoque materia occupatum esse vel certe fuisse, quae me nunc totum tenet. Quid novi inveneris scire gestio. Ego quidem duos jam libros super ea re penè perscriptos habeo quibus et tertius accedet; prior est de refractione planarum et sphaericarum superficierum, et lentium, alter de apparenti augmento vel decremento eorum, quae per refractionem conspiciuntur. In hoc praecipuum est, quod datis positione et figura unâ duabus vel quotcunque lentibus, objecto et oculo, ostendi quo augmento vel diminutione illud conspici debeat, item an erectum an inversum. In illo, datis ijsdem, utrum distincta sit futura visio an confusa. Praeterea ostendi quomodo radios ad datum punctum tendentes ad aliud datum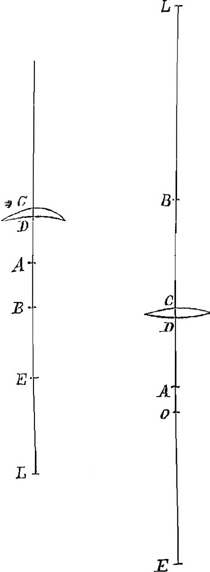



punctum congregare possimus ope superficiei sphaericae, idque accuratè, sicut Cartesius per curvas lineas suas effecit. Cujus quidem principia sequor in demetiendis refractionibus. Cum ad Schotenium nostrum de hoc invento scripsissem⁷⁾ fidem apud ipsum non invenit⁸⁾, putabat enim Cartesium hoc latere non potuisse, nisi esset omnino impossibile; atque etiamnum in sua est opinione, nondum enim demonstrationem exhibui, expectans donec huc excurrat, Caeterum aliquod tibi specimen horum edere volo, quum tam liberaliter egregijs tuis Theorematibus me impertiveris Quomodo in lente inaequalium convexorum punctum concursus radiorum parallelorum inveniri possit frustra quaesivit Keplerus. Id autem sic ego expedio. Esto lens CD, quae vel aequaliter vel inaequaliter convexa sit. sitque A centrum superficiei C, et B superficiei D, et jungatur AB, et producatur utrimque ut tam CE ad EA, quam DL ad LB habeat proportionem refractionis, (haec autem in vitro sesquialtera est ferè, sed paulo major, nam accuratè eam dimetiendo inveni esse quam 600 ad 397) deinde ut EL ad LB ita sit ED ad DO; Eritque O punctum concursus quaesitum, nempe radiorum, qui rectae BA paralleli incidunt, in superficiem C, adeo ut nullius radij concursus cum axe contingat ultra punctum O. Cujus

7) Voyez la Lettre N^o. 130.

8) Voyez la Lettre N^o. 131.

[p. 205]

quidem demonstrationem quum a plurimis Theorematis dependeat, hic non adscribam, neque eam te nunc exigere crediderim. Itaque jam te dimitterem Vir Praestantissime, nisi de inventione tua proportionis Circuli ad Hyperbolam quaedam dicenda occurrerent. Ea quidem verissima est, sed ex annularium tuorum subtilissimis libris, demonstrari nihil opus habet; Enimvero cum ratio circumferentiae ad ⅔ diametri sit eadem quae circuli ad tertiam partem quadrati sibi inscripti, apparet hoc te dicere. Quod videlicet circuli ad hijperbolam proportio, componatur ex ratione circuli ad ⅓ quadrati sibi inscripti, et ex ratione dictae tertiae partis quadrati ad maximum triangulum hijperbolae inscriptum, et ex ratione hujus trianguli ad hyperbolam. Quod sane per se manifestum est, quia positis quotcunque magnitudinibus ratio primae ad ultimam componitur ex ratione primae ad secundam et secundae ad tertiam et ita deinceps donec extiterit proportio. Adeo ut non magis ad hyperbolam Theorema tuum quam ad aliud quodcunque planum spatium pertineat. Illud vero quod subjungis quadraturae Hyperboles, Circuli quadraturam implicari non videri, idem tecum opinor, sed tamen in ea sum opinione utramque parem fere difficultatem habere, adeo ut Soverum, virum doctissimum atque insignem Geometram ut nuper ex opusculo à te citato comperi, etiamsi fata promissum exolvere permisissent, absolutam tamen Hyperboles quadraturam daturum fuisse non existimem. Vides me Batava libertate eorum quae sentio nihil dissimulare Vir Clarissime, atque ubi visum est tibi obloqui; quod te spero non aegrè laturum ita credam non aliter quam si eodem jure in me utentem videro. Vale.

[16] Dec. 1652.