Oeuvres complètes. Tome IV. Correspondance 1662-1663

[p. 81]

N^o 992.
P. de Fermat à [M. Cuzeau de la Chambre].
[Janvier 1662].
Appendice III au No. 989.

La copie se trouve à Leiden, coll. Huygens.

Analysis ad refractiones.

Esto circulus ACBI, cujus diameter ADEB¹⁾ separet duo media diuersae naturae



quorum rarius sit ex parte ACB, densius ex parte AIB. Ponatur centrum circuli punctum D, in quod incidat radius CD, à puncto dato. Quaeritur radius diaclasticus DI, hoc est punctum I, ad quod vergit radius refractus.

Ducantur ad diametrum perpendiculares rectae CF, IH. Cum datum sit punctum C et diameter AB, nec non et centrum D, datur pariter punctum F, et recta FD. Sit ratio mediorum siue ratio resistentiae medij densioris, ad resistentiam medij rarioris, ut recta data DF, ad datam extrinsecus rectam M, quae quidem minor erit rectâ DF, cum resistentia medij rarioris sit minor resistentiâ medij densioris ex axiomate plusquam naturali.

Mensurandi igitur veniunt motus qui fiunt per rectas CD et DI, beneficio rectarum M et DF. hoc est motus qui fit per duas rectas repraesentatur comparatiue per summam duorum rectangulorum, quorum unum sit sub CD et rectâ M, et alterum sub recta DI et rectâ DF. Eo itaque deducitur quaestio, ut ita secetur diameter AB in puncto H, ut ducta ab eo perpendiculari HI, et juncta DI, summa duorum rectangulorum sub CD et M, et sub DI et DF contineat minimum spatium. Quod ut secundum nostram methodum quae jam apud Geometras invaluit et ab Herigono in cursu suo mathematico ante annos plus minus viginti relata est, investigemus, Radius CD datus vocetur N; radius DI erit item N, recta DF vocetur B, et ponatur recta DH esse A, oportet igitur N. M + NB esse minimam quantitatem. Intelligatur quaeuis recta DO, ad libitum sumpta esse aequalis ignotae E, & jungantur rectae CO, OI. Quadratum rectae CO, in terminis analyticis erit N² + E² - 2 BE. Quadratum vero rectae IO

1) Lisez: ADFB.

[p. 82]

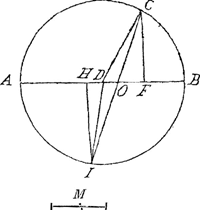
erit N² + E² + 2 AE. Ergo rectangulum sub CO in M, erit in ijsdem terminis radix quadrata M² N² + M² E² - 2 M² BE. Rectangulum vero sub IO in B, erit Radix Quadrata B² N² + B² E² + 2 B² AE. Haec duo rectangula debent ex praeceptis artis adaequari duobus rectangulis MN et BN. Ducantur omnia quadraticè ut tollatur asymmetria²⁾, deinde ablatis communibus et termino asymmetro ex unâ parte collocato, fiet novus ductus quadraticus. Quo peracto et demptis communibus et reliquis per E divisis, ac tandem elisis homogeneis, ab E affectis iuxta praecepta methodi quae dudum omnibus innotuit, et facto parabolismo, fit tandem simplicissima aequatio inter A et M. Hoc est à primo ad ultimum; et ruptis omnibus asymmetriarum obicibus, recta DH, in figura, fit aequalis rectae M. Unde patet punctum diaclasticum ita inveniri. si ductis rectis CD et CF fiat ut resistentia medij densioris ad resistentiam medij rarioris, sive ut B ad M, ita recta FD ad rectam DH, et à puncto H excitetur recta HI, ad diametrum perpendicularis et circulo occurrens in puncto I, quo refractio verget; ideoque radius à medio raro ad densum pertingens frangetur versus perpendicularem. Quod congruit omnino et generaliter invento et Theoremati Cartesiano, cujus accuratissimam demonstrationem à principio nostro deriuatam exhibet superior analysis.

2) De Fermat a en vue la réduction en forme rationnelle.