Oeuvres complètes. Tome II. Correspondance 1657-1659

[p. 435]

N^o 637.
Christiaan Huygens à [R.F. de Sluse].
[juillet 1659.]

La minute et la copie se trouvent à Leiden, coll. Huygens.
La lettre est la réponse aux Nos. 628, 636. R.F. de Sluse y répondit par le No. 641.

Nobilissime Domine

Librum tuum¹⁾ quem jam ad umbilicum perductum existimo per Silvaducenses aurigas expectabo, quando alia opportunitas non datur. lubentissimeque quotquot exemplaria ejus miseris distribuam. In meo²⁾ pauculae adhuc figurae imprimendae restant. Itaque brevi accipies χάλϰεα ἀντὶ χρυσείων videlicet. Quamquam tamen argumenti dignitate confisus Serenissimo Principi Leopoldo magni Etruriae Ducis fratri illum nuncupavi³⁾ gratissimum mihi facies si ostenderis quâ viâ optime deferendum curem, namque et tua ad amicos Florentinos credo missurus est⁴⁾ quibus utinam itineris socius accedam. Dettonvilij inventa merito admiraris; sed et errorem in Theoremate omnium novissimo recte perspexisti, qui emendari tamen potest si unum hoc Theorema aliter concipiatur. admonui jam pridem ea de re autorem, sed Carcavium ab urbe abesse opinor, ad quem literas meas inscripseram⁵⁾. Miror quod scribis te necdum⁶⁾ illa vidisse, quae de Conoidum et sphaeroidum superficiebus inveni. Annus enim atque amplius est cum tibi omnia impertij⁷⁾ teque ea accepisse significasti⁸⁾. Itaque in memoriam redi inveniesque proculdubio in aliqua



mea epistola si quas asservas. De Linea autem Parabolica hujusmodi Theorema est.

Sit Parabolae portio recta ABC, eamque ad terminos basis contingant rectae AD, CD, concurrentes in D. Esto item hyperboles portio EFG, cujus dimidius axis transversus FH aequalis sit basi parabolae AC; tota autem HI quae a centro sectionis ad basin usque portionis extenditur, aequet duas

1) Le ‘Mesolabum’. Voir la Lettre N^o. 563, note 3.

2) Le ‘Systema Saturnium’. Voir la Lettre N^o. 640, note 2.

3) Voir la Lettre N^o. 635.

4) Lisez: es.

5) La lettre de Carcavy dont parle Bouillau dans la lettre N^o. 633.

6) Voir la Lettre N^o. 628.

7) Voir la Lettre N^o. 466 du 26 février 1658.

8) Voir la Lettre N^o. 468 du 4 mars 1658.

[p. 436]

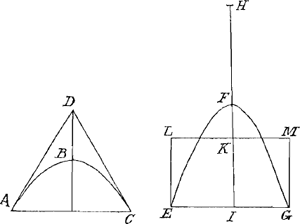
simul AD, DC. Jam si HK aequalis fuerit curvae parabolicae ABC, et ducatur LKM parallela basi EG fiatque parallelogrammum EM eandem cum portione basin habens, cujusque latus basi oppositum transeat per K. Aio hoc ▭ aequale esse hyperboles portioni EFG. Unde itaque connexio quadraturae hyperboles cum dimensione lineae parabolicae manifesta evadit.

Quod si autem novam editionem Geometriae Cartesij quam Schotenius procuravit nondum vidisti est quod tecum communicem insigne inventum juvenis cujusdam nostratis Heuratij nomine. Hic investigans parabolicae lineae mensuram quam mihi inventam resciverat⁹⁾, hanc primum quidem assecutus est, deinde vero ulterius inquirens curvarum quoddam genus reperit (et quidem earum quae Geometricae censentur) quibus rectas lineas absolutè aequales constitui posse docuit. prima earum et simplicissima est paraboloides illa in qua applicatarum ad axem cubi sunt inter se sicut quadrata abscissarum ad verticem. Exemplum adderem sed brevi quid rei sit e libro illo quem dixi addisces, nisi forte jam didicisti. Non est itaque quod ultra naturae repugnare existimes curvam rectae aequalem inveniri¹⁰⁾.

9) Consultez la Lettre N^o. 587.

10) Voir la dernière phrase de la pièce N^o. 614.