Oeuvres complètes. Tome II. Correspondance 1657-1659

N^o 614.
A. Dettonville [Bl. Pascal] à Christiaan Huygens.
[janvier 1659.]
Appendice au No. 613.

La pièce a été imprimée dans les Lettres de A. Dettonville. Paris 1659.

Dimension des lignes covrbes de toutes les Roulettes.

Ie n'ay qu'vne seule methode pour la dimension des lignes de toutes sortes de Roulettes; en sorte que soit qu'elles soient simples, alongées ou accourcies, ma construction est tousiours pareille, en cette maniere.

Soit, vne Roulette de quelque espece que ce soit, dont AF soit la base, FC l'axe, & CMF la circonference du cercle generateur, laquelle ayt telle raison qu'on voudra à la base FA, & ayant diuisé sa circonference en vn nombre indefiny d'arcs égaux aux points M, ie mene de tous les points de diuision des droites MB, paralleles à la base, qui coupent la courbe de la Roulette chacune en vn point B, & ie ioints tous les points voisins BB.

Ie suppose que les diuisions de la circonference soient en si grand nombre que la somme de ces droittes BB (lesquelles sont les soustendantes de la Roulette) ne different de la courbe de la Roulette, que d'vne ligne moindre qu'aucune donnée.

I'ay aussi besoin qu'on sçache (& ie le monstreray en peu de mots) que si on fait, comme la circonference du cercle generateur à la base de la Roulette, ainsi le rayon FG, à la portion GH de l'axe prise depuis le centre: Et que de l'extremité H de cette portion on mene toutes les droites HM: Il arriuera que toutes ces droites seront entre elles, comme les soustendantes BB de la Roulette, & qu'elles les representent: & c'est pourquoy ie les appelle les representantes.

Cela sera visible, si on entend que le cercle generateur soit placé à tous les

[p. 398]

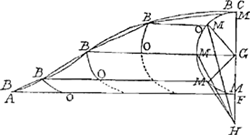
points B, lequel coupe chaque parallele BM voisine, au point O; en sorte qu'on en considere que les arcs BO, lesquels seront esgaux tant entre eux qu'aux arcs MM, & les portions BO des paralleles seront esgales entre elles. Et ainsi chaque arc BO sera à la portion OB de la parallele, comme la circonference FMC, à la base AF, ou comme GM à GH. Et il arriuera ainsi que chacun des petits triangles BOB sera semblable à chacun des triangles MGH: chacun des angles HGM, estant esgal à chacun des angles BOB, ou BMC, faits de chaque parallele & de la circonference. Et partant chaque BB sera à chaque arc BO, comme chaque HM à MG. Et toutes les BB ensemble, c'est à dire la courbe, sera à tous les arcs esgaux ensemble OB ou MM, c'est à dire à la circonference CMF, comme la somme des HM, à la somme des GM, ou au rayon multiplié par la circonference CMF. Donc en multipliant les deux premiers termes par le rayon, la courbe multipliée par le rayon, est à la circonference CMF multipliée par le rayon, comme la somme des representantes HM, au rayon multiplié par la circonference CMF: mais les deux consequents sont esgaux: donc la courbe multipliée par le rayon, est esgale à la somme des representantes HM (multipliées chacune par les petits arcs MM) mais le rayon est donné: donc si la somme des HM est donnée, la courbe le sera aussi.

Donc toute la difficulté de la dimension des Roulettes, est reduite à ce probléme.

La circonference d'vn cercle donné estant diuisée en vn nombre indefiny d'arcs esgaux, & ayant mené des droites d'vn point quelconque donné dans le plan du cercle à tous les points de diuision: Trouuer la somme de ces droites.

Ce probléme est aisé à resoudre quand le point donné est dans la circonference, (comme il arriue quand la Roulette est simple; c'est à dire quand la base AF est égale à la circonference CMF:) car alors la somme de ces droites est esgale au quarré du diametre, parce que c'est la mesme chose que la somme des sinus droits du quart d'vn autre cercle, dont le rayon sera double.

Et si on resout ce probléme quand le point donné est au dehors, il sera resolu en mesme temps quand le point est au dedans.

Car s'il y a deux cercles concentriques, dont les circonferences soient diuisées chacune en vn nombre indefiny d'arcs esgaux: la somme des droites menée d'vn point quelconque de la grande circonference, à tous les points de diuision de la petite, sera la mesme que la somme des droites menées d'vn point quelconque pris dans la petite circonference, à tous les points de diuision de la grande: Et chacune des droites d'vne multitude sera esgale à chacune des droites de l'autre multitude, parce qu'elles sont les bases de triangles égaux & semblables. Et ainsi la somme des vnes sera égale à la somme des autres, pourueu qu'elles soient multipliées par les mesmes arcs. Mais si on entend qu'elles soient multipliées chacune par les arcs ausquels elles se terminent, alors la somme de celles qui sont menées aux diuisions de la grande circonference, sera à la somme des autres, comme la grande circonference est à l'autre, ou comme le grand rayon au petit. Et ainsi si la somme des vnes est donnée, la somme des autres le sera aussi, les deux cercles estans donnez.

[p. 399]

Or i'ay ce Theoréme general.

La circonference d'vn cercle donné estant diuisée en vn nombre indefiny d'arcs esgaux, & vn point quelconque estant pris où l'on voudra, soit en la circonference, soit dedans, soit dehors, soit sur le plan, soit hors du plan, d'où soient menées des droites à tous les points de diuision. Ie dis que la somme de ces droites sera esgale à la surface d'vn Cylindre oblique donné.

Et ie le demonstre en cette sorte dans le cas où le point est pris hors du cercle, qui est le seul dont i'ay besoin icy, & duquel s'ensuiuent tous les autres.

Lemme.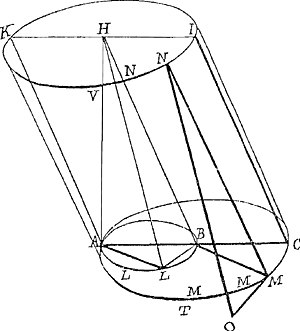

Soit le cercle donné ALB, dont la circonference soit diuisée en vn nombre indefiny d'arcs égaux en L. Soit le point H hors du plan, & esleué perpendiculairement sur vn des points A, c'est à dire que la droite AH, soit perpendiculaire au plan du cercle: & soient menées toutes les HL. Ie dis que la somme des droites HL multipliées chacune par chaque petit arc LL, est esgale au quart de la surface du Cylindre oblique, qui aura pour base le cercle AMC, dont le rayon sera de AB, & pour axe la droite HB, menée à l'autre extremité du diametre AB.

Car soient les costez du Cylindre oblique MN, qui coupent la base superieure en N: & soient MO les touchantes de la base inferieure, sur lesquelles soient menées les perpendiculaires NO. Il est visible que le quart de la surface oblique IVTC, est composée des parallelogrames compris des arcs MM & des costez MN, ou des rectangles compris des mesmes arcs MM, & des perpendiculaires NO: mais les arcs MM sont egaux tant entre eux qu'aux arcs LL: donc si la somme des perpendiculaires NO, est égale à la somme des droites HL, ce qui est proposé, sera euident.

Or chaque NO est esgal à chaque HL, comme il est visible par l'esgalité & la similitude des triangles HBL, NMO.

Car l'axe HB est esgal & parallele au costé NM, & les droites BL, MO sont paralleles estant perpendiculaires l'vne à MB, l'autre à AL qui sont paralleles à cause de l'esgalité des angles CBM, BAL.

[p. 400]

Proposition.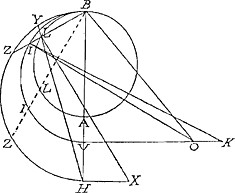

Soit maintenant le point H donné dans le plan du cercle ALB, & hors le cercle, & soient menées les HL, aux points L des diuisions esgales.

Ie dis que leur somme est esgale à la surface d'vn Cylindre oblique.

Car en menant le cercle dont BH est le diametre, & prenant AV, en sorte que BV quarré, soit esgal à BA quarré, plus deux fois le rectangle BAH, & menant le cercle dont BV soit diametre: & où il arriuera aussi que quelque droite qu'on mene du point B, comme BLIZ, le quarré de BI, sera esgal à BL quarré, plus deux fois le rectangle BLZ.

Soit aussi esleué VO perpendiculaire au plan du cercle, & soient prises BO égale à BH, & soient menées toutes les droites OI, (aux points où les droites BL coupent la circonference CIV)¹⁾ Ie dis que chaque droite OI est esgale à chaque droite HL.

Car HB quarré est égal à HL quarré, plus LB quarré, plus deux fois le rectangle HLY (en prolongeant HL iusqu'au cercle BZH) ou à HL quarré, plus LB quarré, plus deux fois le rectangle BLZ, ou à HL quarré, plus BI quarré: mais aussi OB quarré (qui est le mesme que HB quarré) est esgale à OI quarré, plus BI quarré: Donc OI quarré plus IB quarré est esgal à HL quarré plus IB quarré: Donc aussi OI quarré est esgal à HL quarré: & partant OI à HL.

Donc la somme des OI est la mesme que la somme des HL. (si on les multiplie chacune par les mesmes petits arcs) mais la somme des OI (multipliée par les petits arcs II, lesquels sont esgaux entre eux, puis que les arcs LL le sont par l'hypothese) est esgale au quart de la surface d'vn Cylindre oblique par le Lemme, puis que VO est perpendiculaire au plan du cercle BIV.

Donc la somme des HL multipliée par les mesmes arcs II, est esgale au quart de la mesme surface. Donc la somme des HL multipliée par les petits arcs LL, est aussi égale à vne surface d'vn Cylindre oblique proportionnée à l'autre. Ce qu'il falloit demonstrer.

On demonstrera la mesme chose, si le point donné X, est pris hors du plan, & esleué perpendiculairement sur le point H.

Car en prenant dans la perpendiculaire VO le point K, en sorte que KO quarré, plus deux fois le rectangle KOV, soit esgal à HX quarré. Il est visible que toutes

1) Lisez: BIV.

[p. 401]

les XL seront esgales à toutes les KI, chacune à la sienne, puis que chaque XL quarré, ou XH quarré, plus HL quarré, sera esgal à chaque KI quarré ou OI quarré (qui est esgale à HL quarré) plus KO quarré, plus deux fois KOV qui sont pris esgaux à XH quarré.

Donc la somme des XL est esgale à la somme des KI, laquelle est égale à la surface d'vn Cylindre oblique par le mesme Lemme.

Conclusion.

De toutes lesquelles choses il s'ensuit que la somme des HL des representantes estant égale à la surface d'vn Cylindre oblique, elle sera par consequent égale au rectangle qui a pour hauteur l'axe du Cone oblique, & pour base la courbe de l'Elipse engendrée dans la surface du Cylindre oblique par le plan perpendiculaire à l'axe. Or la mesme somme des representantes, est desia monstrée esgale à la courbe de la Roulette multipliée par le rayon de son generateur. Donc la courbe de la Roulette multipliée par le rayon, est esgale à la courbe d'vne Elipse multipliée par l'axe d'vn Cylindre oblique donné. Donc comme l'axe du Cylindre (donné) est au rayon (donné) ainsi la courbe de la Roulette est à la courbe d'vne Elipse. Ce qu'il falloit demonstrer.

En suiuant cette methode, on trouuera le calcul des deux axes de l'Elipse, dont la courbe se compare à celle d'vne Roulette donnée. Le voicy tel que ie le fis enuoyer à beaucoup de personnes, au commencement de Septembre, en Angleterre, au Liege, & ailleurs, & entr' autres à Monsieur de Roberual, à Monsieur de Sluze, & quelque temps apres à Monsieur de Fermat.

Soit fait comme la circonference du cercle generateur, à cette mesme circonference plus la base de la Roulette, ainsi le diametre du cercle à vne autre droite: Cette droite soit le grand demy axe d'vn Elipse. Soit fait comme la circonference plus la base, à la difference entre la circonference & la base, ainsi le grand demy axe à l'autre demy axe. La moitié de la courbe de l'Elipse qui aura ces deux demy axes, sera esgale à la courbe de la Roulette entiere, & les parties aux parties.

On conclura aussi de tout ce qui a esté monstré; Que deux Roulettes, l'vne alongée, l'autre accourcie, ont leurs lignes courbes esgales entre elles, s'il arriue de part & d'autre que la base de l'vne soit égale à la circonference du cercle generateur de l'autre.

Il me seroit aisé de reduire cette methode à la maniere des anciens, & de donner vne demonstration pareille à celle que i'ay faite de l'Egalité des Lignes Spirale & Parabolique: Mais parce que cela seroit vn peu plus long & inutile, ie la laisse, quoy que ie l'aye toute preste, & ie me contente d'en auoir donné cet exemple de la Spirale & la Parabole.

On voit aussi par toutes ces choses, que plus la base de la Roulette approche d'estre esgale à la circonference du cercle generateur, plus le demy axe de l'Elipse qui

[p. 402]

luy esgale, deuient petit à l'esgard du grand axe: & que quand la base est esgale à la circonference, c'est à dire quand la Roulette est simple, le petit axe de l'Elipse est entierement aneanty: & qu' alors la ligne courbe de l'Elipse (laquelle est toute applatie) est la mesme chose qu'vne ligne droite, sçauoir son grand axe: Et de là vient qu'en ce cas la courbe de la Roulette est aussi esgale à vne ligne droite. Ce fut pour cela que ie fis mander à ceux à qui i' enuoyay ce calcul, que les courbes des Roulettes estoient tousiours par leur nature, esgales à des Elipses, & que cette admirable esgalité de la courbe de la Roulette simple à vne droite que Monsieur Wren a trouuée, n'estoit pour ainsi dire, qu'vne esgalité par accident, qui vient de ce qu'en ce cas l'Elipse se trouue reduite à vne droite. A quoy Monsieur de Sluze adiousta cette belle remarque, dans sa responce du mois de Septembre dernier, qu'on deuoit encore admirer sur cela l'ordre de la nature, qui ne permet point qu'on trouue vne droite esgale à vne courbe, qu' apres qu'on a desia supposé l'esgalité d'vne droite à vne courbe. Et qu' ainsi dans la Roulette simple où l'on suppose que la base est esgale à la circonference du generateur, il arriue que la courbe de la Roulette est esgale à vne droite.