Oeuvres complètes. Tome II. Correspondance 1657-1659

N^o 444.
Christiaan Huygens à Fr. van Schooten.
28 décembre 1657.

La lettre, la minute et la copie se trouvent à Leiden, coll. Huygens.
Elle est la réponse aux Nos. 434 et 440. Fr. van Schooten y répondit par le No. 457.

Domino Fr. Schotenio Viro Clarissimo Chr. Hugenius S.D.

Binis tuis responsum debeo, quarum alterae¹⁾ Domini Huddenij Heuratijque literas inclusas²⁾ ferebant, quas ecce tibi restituo, alterae à Domino van Loon mihi traditae³⁾. His iteratò petis à me ut microscopij mei usum tibi commodem: quod equidem misissem tibi continuo si penes me habuissem. Verum illud mihi Dominus Vossius⁴⁾ abstulerat paucis ante diebus, quàm te desiderare intellexi; neque adhuc repetere audeo, ne fortasse et ipse a me repetat Pappi⁵⁾ exemplar graecum manuscriptum, cujus mihi copiam fecit. Rogo itaque ut paucorum adhuc dierum moram perferas. nam fratris mei perspicillum ejus generis, quod tibi mittere decreveram, nequaquam tam bonum atque meum esse experior. Inventum nuperum Domini

1) Voir la Lettre N^o. 434.

2) Voir les Lettres N^os. 436, 437, 435.

3) Voir la Lettre N^o. 440.

4) Isaac Vossius, fils du Professeur Gerardus Johannes Vossius et de Elisabeth Junius, naquit à Leiden en 1618 et mourut à Londres le 22 février 1689. Dans ses voyages il rassembla beaucoup de manuscrits; il s'établit d'abord à Amsterdam, plus tard il se rendit en Suède, où, de 1648 jusqu'à 1654, il vécut à la cour de la reine Christine. Comme la reine, après son abdication, ne remboursait pas le prix des manuscrits que Vossius avait achetés pour elle, il retourna en Hollande, emportant deux caisses remplies des pièces les plus précieuses. En 1663 il était à Paris, en 1670 il passa à Londres, où on lui conféra le canonicat de Windsor; l'offre de vente de sa bibliothèque, riche surtout en manuscrits grecs et latins, fut refusée par les savants d'Oxford; après sa mort, la collection fut achetée par les Etats de Hollande pour l'Université de Leiden.

5) C'est sans doute le Manuscrit de la Bibliothèque de Leiden, actuellement Codex Vossianus Graecus. in-folio. N^o. 18.

[p. 111]

Heuraet de quo inaudisse scribis pulcherrimum sanè videtur. Sed praecisius scire velim ad quas lineas pertineat, namque etsi verisimile est aliarum quadraturam esse possibilem, aliarum vero non item; nullum tamen certum indicium reperiri crediderim earum quae quadraturam non subeant. Sunt parabolarum vel paraboloidum innumerae species de quibus Mersennus in praefatione mechanicorum⁶⁾ quae omnes per regulam ibi traditam quadrantur, cujus quidem regulae demonstrationem haud vulgarem inveni non ita pridem. Praeter istas verò nullam curvam novi cujus dimensio adhuc reperta sit. Nam quae ab Huddenio propositae sunt, uti et Slusiana illa, ipso docente Huddenio, non sunt pro novis habendae, sed ex ijs quas dixi paraboloidibus effictae. Quod si tamen hoc modo genitas (nam variae atque admodum intricatae proferri possunt) continuò ad rectilineum reducere novit Heuratius, subtile admodum, ipsoque dignum est repertum. Saepe quidem illum depraedicare te mihi nemini, et planè insigni ingenio esse vel ex ijs perspicio quae de Slusij curva rescripsit. Illud enim praeclarè quod et quadraturam et centrum gravitatis totius lineae et partium, ex ipsius lineae proprietatibus investigavit, nullius parabolae adscita consideratione. Idque ratione adeo subtili, praesertim in ijs quae ad centrum gravitatis attinent, ut methodum ipsius assequi, vel ex ijs quae tradidit, non vulgaris sit artificij. Magis apertè suam explicuit Clarissimus Huddenius, nam posteaquam ostendit unde ortum haberet Slusij linea, manifesta ac facilis evadit eorum omnium inventio, quae circa illam quaerenda proponebantur. Verum id ipsum reperisse eximium est. Nam me quidem fateor hoc non animadvertisse, Slusii curvam partem esse parabolae cubicae abscissae aliâ simplici parabolâ; quadraturamque ejus et centrum gravitatis nullo parabolae cubicae respectu adinveni. Existimo autem et ipsum Slusium nescivisse hanc suae originem esse lineae, quoniam alioqui de tertia illa vestra jure causari non potuisset quod pars esset curvae ab alijs pridem explicitae. Hoc autem ex ipso Domino Slusio brevi resciscam; cui praecipua quaeque ex prolixa Huddenij epistola transcripta impertij, omissis tamen quae vel minimum offensae parere posse videbantur, ne ex contentione simultas tandem oriretur inter viros tam bene de studiis Geometricis merentes. Apologia quidem adversum nos nihil opus erat Domino Huddenio, cum neuter illum incusaverit, quasi ultrò larvam opposuisset curvae suae secundae, quo nobis molestiam crearet. Verum cum larvam dicebamus, illud quod res erat suspicabamur, nimirum ex alijs quibusdam satis notis lineis hanc efformatam esse, quod tamen quâ ratione facere instituisset ex aequatione illa aegrè deprehendi

6) Euclidis Elementorum Libri, Apollonii Pergaei Conica. Sereni de Sectione Coni & Cylindri. Archimedis Opera. Theodosii, Menelai et Maurolyci Sphaerica & Cosmographica. Mechanicorum Libri. Commandini et Lucae Valerii Libri de centro gravitatis solidorum. Auct. M. Mersenne. Parisiis. 1626. 3 Vol. in-8^o.
M. Marini Mersenni Minimi Tractatvs Mechanicvs theoreticvs et practicvs. Parisiis, Sumptibus Antonii Bersier, viâ Jacobaeâ, sub signo Fortunae. m.dc.xliv. Cvm Privilegio Regis. in-4^o.
Ce dernier ouvrage fait aussi partie de l'ouvrage cité dans la Lettre N^o. 21, à la Note 2.

[p. 112]

posset, nisi divinando fortasse atque omnia experiendo. Ignoratâ autem illâ lineae origine quadraturam aliunde haberi non posse non immerito arbitrabamur. At in Slusij curva aliter se res habebat, siquidem diversis vijs, ut eventus docuit eo perveniri poterat: ut proinde ille novam se lineam invenisse existimaverit, cujus dimensio ab aliarum dimensione non penderet, quaeque ideo contemplatione digna esset. Sin contra esse conscius sibi fuit, tum ipsum quoque larva tectam nobis adduxisse dicam. Centrum gravitatis primae lineae suae miratur Huddenius me non invenisse. Ego verò si ipse invenerit mirabor. Etenim nisi fallor, non rectè animadvertit quid hic à nobis exegerit. nam spatij quidem 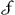Gf centrum gravitatis in diametro G facile



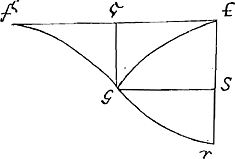reperitur, at nequaquam spatij fGS, vel ejus dupli fGr in diametro GS, quod nobis propositum fuit. Itaque vereor ne illud tantum invenerit.

Tangentes alias quam ex punctis in peripheria curvarum non quaesivi, quoniam postulari nesciebam. nam quod Dominus Huddenius alteras quoque illas ad curvam Slusij addiderat, credebam id eum auctarij vice, ut alia multa corollaria, admensum esse. Nec tamen difficile fuisset aequationem dare quae tangentis ejusmodi constructionem complecteretur, sicut ab ipso factum videmus.

Quod de delectu problematum scripseram, verum aequumque esse fatetur, sed ita, ut quodammodo stomachari interim videatur. Sed ego haec transeo, quoniam disceptationibus hujusmodi pejus adhuc tempus teri arbitror, quam inutilibus quaestionibus immorando. Neque ista omnia tanti sunt, ut propterea Huddenio minus amico utar, quem merito suo permagni facio, ac pridem summis Geometris accenseo. Eorum quae circa Parabolam noviter invenisse me significavi, alterum tibi aperiam, alterum adhuc certam ob causam celabo. Reperi itaque quomodo datae superficiei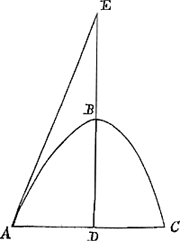



conoidis parabolici circulus aequalis exhiberi possit. Et convexam quidem conoidis superficiem ad circulum baseos esse ut numerus ad numerum, quoties basis parabolae quae fit sectione per axem conoidis, commensurabilis est rectae tangenti ipsam in termino baseos atque ad axem terminatae. Ut si sit conoides cujus sectio per axem parabola ABC, cujus axis BD: fuerit autem basis AC commensurabilis tangenti AE. Dico superficiem quoque conoidis convexam ABC ad circulum cujus diameter AC, fore ut numerus ad numerum. Nempe si AE sit aequalis AC, erit dictae superficiei ad dictum circulum ea ratio quae 14 ad 9.

[p. 113]

Si vero AE sesquialtera AC, erit ea, quae 13 ad 6.

Vale Vir Praestantissimè, et mihi quoque si quid habes rei novae impertire.

Hagae Com. 28 Dec. 1657.

Ecce perferuntur ad me Domini Slusij literae⁷⁾ quas operaepretium visum est tibi et per te Domino Huddenio ostendere, itaque illas una mitto.

7) C'est la Lettre N^o. 441.