Oeuvres complètes. Tome II. Correspondance 1657-1659

(1889)–Christiaan Huygens– rechtenstatus


N^o 436. J. Hudde à Fr. van Schooten. 1 décembre 1657. Appendice II au No. 434. La copie se trouve à Leiden, coll. Huygens. Copie. Mijn Heer en bezondere Vriend F.v. Schoten. Eergister avond ben ick van myn reis eerst thuijs gekomen, andersints had ick u.E. al eer op den brief van Jonkheer van ZuijlichemGa naar voetnoot1) geandwoordt, in welcke ick zie dat zijn Ed. en Domini Slusij antwoord op mijn 3 voorgestelde kromme lijnen vervat word. Op mijn j^ste vind ick dat Dominus Sliusius ⁸) de Tangens, door een punt in de peripherie gegeven, toont, als mede Jonkheer van Zuijlichem. 'T geeft my wonder datze 't alleen door een punt inde peripherie toonen, en uit een punt daer buijten voorbijgaen, dewijl 't methodus om dat te vinden al over lange bij andere is aengewesen, en tot dien einde nu alleen nodig d' eerste beginselen vande Geometrie te weten, en algebraicè te konnen calculeren, derhalven als ick geeist heb de Tangenten zo heb ick voornementlyck gesien op 't geen sy hebben overgeslagen: en ick wil wel bekennen, dat ick kunstiger oordeel de Tangenten uyt een punt buiten de peripherie wel te trecken, als de Quadratura en centra gravitatis van Domini Slusij en al myn krommen gesamentlyck, te vinden. De Quadratura zoze by Dominum SliusiusGa naar voetnoot2) word aangewezen is goet, maer ick verwonder my over dese woorden Quoniam res prolixa est, &c. contentus ero unico exemplo rem arithmetice, declarare. die van Jonkheer van Zuilichem bevin ik met de myne over een te komen. Vant centrum gravitatis vind ik by Dominum Slusius niet een
[pagina 98]
eenig woord, als mogelik dat dese, ulterius in hanc inquirere non vacavit; daer op zien. En zeker hy doet niet qualick, maer mijns oordeels wonder wel, zo hy zich niet laat van nodiger dingen hier door aftrecken: en die altijt het onnodiger voor 't nodiger kost opschieten souw sonder twijfel groter dingen doen als deze, ja als hondert duijsent diergelycke centra te vinden. Maer ick ben verwondert dat Jonkheer van Zuylichem seidt, dat hy 't Centrum tot noch toe niet had konnen vinden. Op myn 2^de is by d' een noch d' ander iets gedaen, 't schuynt datse door de groote equatie vervaart syn geworden, evenwel heb ick hier 't meest op te seggen, niet om dat haer Ed. deselve hebben overgeslagen, maer om datse my van een misslagh beschuldigen, dien ick de grootste acht, die ontrent het voorstellen van eenige Problemata begaan kan worden, en van welcke ik gansch zuyver ben. Zij meynen dat ick met voordacht dese equatie zo hooch gemaeckt heb, 't welck tot geen ander eynde souw hebben konnen geschieden als om haer aen groote moeyte te helpen, en dat in een saak die anders, ontbloot van dit mom-bakkis, veel lichter zouw vallen. Zeker dat ik so een pedant niet ben, haddenze genoechsaem in de solutie op haer problema en uitde manier van voorstellen van de mijne en insonderheyt vande 3^e (dien ik met weinich moeite so een mom-aansicht had konnen voordoen, ja zulk een ook, dat Dominus Slusius haer aen het wesen gantsch niet souw gekent hebben.) konnen afnemen. Alzo seer als een van haer Ed. haet ik dusdanige gemaskerde zotten, en also weinich sal ik de goede uuren van doorluchtige verstanden, op die wijs soecken te stelen, en met grooter harts-tocht, geloof ik, bemin ik problemata van kunst, weinigh rekenings, en gevolgen waerdig om te weten; ik zal er noch by voegen, en daer 't gemeen eenige vrucht van te hoopen heeft, Voorts hoe licht en kort de calculatie vande Quadratura en Centrum Gravitatis valt sal het volgende methodus aanwijsen, als mede toonen datze niet vermomt, maer zo naekt alsze van de moêr geboren is, haer rol gespeelt heeft. Op mijn 3^e en laeste heeft Dominus Slusius aangetekent, dat hy uit de equatie zelfs zonder eenige andere werking gesien heeft, datse t' zaam gestelt was ex partibus curvae, cujus dimensio, tangens, centrum gravitatis dudum ab aliis ostensa sunt, en derhalven dat hy niet en wil πολυπραγμωνεῖν in re jam peracta. Hier ben ik niet weinich verwondert dat hy dit uit deze equatie heeft konnen mercken gelijck oock Jonkheer van Suilichem, en datse evenwel niet gemerckt en hebben uit d'equatie van myn j^e, dat dese j^e maar een stuk was van hare eigen voorgestelde kromme, 't welk myns oordeels nochtans lichter te sien is, en daarenboven dat de haare oock niet meer als een stuck is van een parabola cubica, waer van de quadratura, centrum gravitatis, en dat de tangenten al eerder gevonden syn, als van die parabola waar van mijn 3^e een gedeelte is. Voorts heeft 'er Jonkheer van Zuylichem by gedaan de constructie door een punt inde peripherie gegeven, als mede de Quadratura en Centrum gravitatis welcke laasten goet syn, en aende Tangens twijfel ik niet maer heb deselve niet naa gerekent, gelijck oock niet de tangenten op d' j^ste.
[pagina 99]
Nu zal ik overgaan tot myn methodus, En op dat ick niet soude πολυπραγμωνεῖν in re jam peracta so heb ik gepresupponeert 't geen aengaende de Quadratura en centra gravitatis van alle parabolaas by Merzenne voor aen inde praefatione in librum mechanicum gevonden word. Sy derhalven ADC een Parabola, AB de diameter, waar van de □^ta op de semiordinaten DP en CB tot elkander staan als 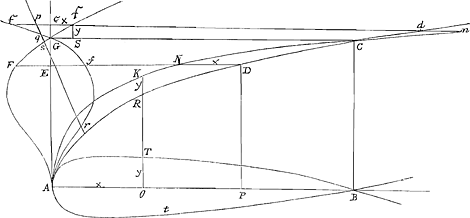AP tot AB. sy oock AKCn een parabola cubica, waar van de cubi op de semiordinaten KO, CB tot elkander staan als AO. tot AB, zy voorts Ac paralleel met BC, en DF, GC, cn met AB, somen nu neempt EF ∞ DN ∞ x. GE ∞ y en AB ∞ BC ∞ a, so heeft men dese equatie aax ∞ y³ 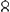Ga naar voetnoot3) 2 ayy + aay, en so E valt tusschen G en A, zo krijgt men aax ∞ y³ - 2 ayy + aay welcke de aequatie is op de kromme door Jonkheer van Zuylichem of Dominus Slusius voorgestelt; so E valt aan d'ander zyde, so heeft men aax ∞ y³ + 2 ayy + aay welcke is d'aequatie van mijn eerste kromme zijnde G 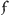S. maer so men de relatie maakt tot de diameter AB, nemende OT ∞ RK ∞ y en AO ∞ x, dan heeft men deze equatie y⁶ - 3 axy⁴ - 2 aaxy³ -Ga naar voetnoot4) 3 aaxxyy - 6 a³ xxy + a⁴ xx - a³ x³ ∞ 0, zijnde d'aequatie van mijn 2^de kromme dien vreeslycken Bulle-bak ATBt, wiens quadrature is evengroot als haere AFG f, en als de differentie van beide parabolaas AKCDA; dat nu weijnich moeijte heeft te vinden, bekent gestelt synde, gelyck an de Heeren bekendt was, de Quadratura van de parabolaas; gelyck ook het
[pagina 100]
Centrum gravitatis van deselve op de nagel van mijn duym kan gerekent worden, wanneer men insgelijcx presupponeert, tgeen by andere nu al overlang gevonden en bij haer Ed. niet onbekent was, de vinding namentlyck van de Centra Gravitatis illarum parabolarum. Zulx dat hier dan klaar blijkt, dat ick niet gesocht heb haer aen veel moeijtens te helpen, en de dingen met voordacht sonder de kunst te vermeerderen, zwaarder te maaken, en also de tijd van zulke brave geesten onnuttelijcke en met verdriet te consumeren, en zeker, tzouw een wonder onnosel concept geweest syn, want wat stond mij in toekomende, wanneer haer d'auteur mocht bekent geworden syn, anders daer uyt te verwachten als een rechtvaerdigen haet etc. Zy hadden veel eer behooren gedacht te hebben, daerse zagen dat mijn 3^de maer een gedeelte was van een parabola, dat ook alle d'andre en de hare maar stukken waren, en dat d'auteur dezelve tot sulken einde alleen daerby gevoecht hadde alsmen een aen een wegh stelt, op datse daer door mogten sien wat wech ick ingeslagen had, en welke zoze involghden, haar niet alleen wees hoe men gemakkelyck de Quadratura en Centrum gravitatis van haar voorgestelde kromme kost vinden, maer oock hoe men oneindige diegelycke kromme kost maken, en derselver Quadratura en Centra op dezelve manier ontdekken: want blijvende deselve parabolaas, zo kan men 'er verscheide vinden door de verscheide relatien, gelyck getoont is, en nemende voor de parabola Cubica een ander van hoger geslacht, de parabola quadratica blijvende, zo krygt men weder andre; gelyck oock sij ende ieder derselven of door een ander parabola van lager geslacht, als nemende slechts twe na welgevallen uit de parabolaas en die op de geseijde wys nu gegenereert sijn: en niet alleen dat men van jeder derselve de Quadratura en Centrum kan vinden ten opsichte van hare heele figuer, maer oock van jeder stuck na welgevallen afgesneden, als by exempel van het stuck AFsr en 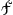pq gezamentlick of ook apart, gelijck uE voordesen oock geschreven hebbe. Twelck alles so licht uit dit methodus vloeit dat ick oordeelen souw mijn tijt onut besteden so ick het selve met meerder woorden socht aen te wijsen. Hoewel ik geloof, dat zoge haer Ed. dit bekendt maeckt, datze dan wel zien sullen, dat ik mijn kromme niet gemaskert heb op 't tonneel gebracht, om haeren arbeidt soo vruchteloos te rooven, evenwel zo zal ik 'er dit noch byvoegen, dat ik in tegendeel, om deselve te verlichten AB heb genomen ∞ BC, welke positie tot geen ander einde dient als om grooter calculatien af te snyden: en om haer voorgestelde kromme van dezelve gedaante te hebben alsze by haer is voorgestelt, men AB moet neemen ∞ 8FE zynde dan AE ∞ EG, zulx dat AB hier grooter of kleender kan syn als BC. Eindelick op de woorden van Jonkheer van Zuylichem: Ejusmodi vero Problematis quae prolixum calculum minantur, neque egregiam prae se ferunt utilitatem non libenter bonas horas impendo. Ideoque ea tantum mihi proponi velim quaerenda, quibus inventis operaepretium me facturum, atque aliquid scitu dignum consecuturum intelligam; antwoord ik alleenlick, dat ik hem daer in gelijck geef, maer so hy acht dat hy daer tegens
[pagina 101]
niet gesondicht heeft, toen hy ons de kromme van Dominus Slusius voorgaf, dat ik dan in allen geval daer tegens niet mis daen hebbe, dewijl ick hem door middel van myn Problemata in een methodus heb willen inleijden, waer door men niet alleen seer licht de Quadratura en Centrum gravitatis van syn voorgestelde kan oplossen, maer oock van oneindige andere diergelycke, ja van alle, die uijt de sectie van twee kromme, waervan de Quadratura en Centrum gravitatis bekent syn, uytspruyten, en dat zo wel van haer gehele figuere als van eenige na welgevallen afgesneden stukken, gelyck hier voren geseijdt is, sulx dat ik niet en weet wat'er ontrent dese zaak meerder zouw konnen begeert werden, ten waere dan dat ment wilde uitstrekken tot de lichaamen, welcke uijt dese figuiren gemaackt konnen werden, twelck ik de moeite niet waerdich acht om na te dencken, hoewel ick op staende voet wel sien kan, datmen op gelijcke manier, of met weinich verschil, uyt de sectie van twee corpora, waervan de relatie tot een cijlinder of conus, en de centra gravitatis bekent zijn, oneindig andere kan maken, van welcke men insgelijcx de relatie tot een cylinder of conus, en 't centrum gravitatis zeer licht kan vinden. Ick houw my dan overvloedig gezuijvert. Maar nu versoeck ick, datse my noit diegelycke problemata weer komen voor te stellen, dewijl ick de tyd veel te kostlijck acht, als dat ickse in soodanige nutteloose questien zouw besteden; en ik wens haer Ed. toe, nevens een lang en gesond leven, datze niet alleen ter hand mogen nemen sodanige Problemata ubi inventio praecipua est, et calculus non difficilis, sed etiam utilis humano generi, en datze alle andre standvastelijck vander hand afwijzen, en ons also in plaats van vruchteloose questien, die niet een olykoeck waert zyn, mogen aanden dach brengen en solveren soodanigen daer het gemeen aen gelegen is, dewijl 'er van dien aart noch genoech te vinden zijn, maer dese afgedaen synde, dan zal ik 't niet qualik nemen datse tot andere, die alleen in speculatie bestaen, overgaen. Jmmer ik ben geresolveert dit, zoot' in mijn macht is, op het naukeurigste te practiseren. Eindigende, zal Ed. Gode bevelen, en zijt, nevens alle de vrienden hertelijck gegroet van UE. seer geaffecionneerde vriend en Dienaar Johannes Hudde. Amst. 1 xbr. 1657.	voetnoot1) Voir la Lettre N^o. 431. voetnoot2) Lisez: Slusius. voetnoot3) C'est le signe pour ±. voetnoot4) Lisez: +.