Oeuvres complètes. Tome II. Correspondance 1657-1659

[p. 89]

N^o 431.
Christiaan Huygens à Fr. van Schooten.
23 novembre 1657.

La lettre, la minute et la copie se trouvent à Leiden, coll. Huygens.
Elle est la réponse au No. 419. Fr. van Schooten y répondit par le No. 434.

Clarissimo Viro Domino Fr. Schotenio Chr. Hugenius S.

Problemata circa curvas lineas quae Geometrae vestri mihi proposuere Domino Slusio communicanda¹⁾ existimavi; à quo cum huc usque responsum expectaverim, nunc eo²⁾ accepto, quid ille quidque ego invenerimus tibi exponam. Prius tamen hoc scito, cumulatè satisfactum nobis esse ijs quas misisti solutionibus ut et expostulare tecum lubeat, quod eximiorum virorum³⁾, quibus discipulis gloriari debebas, ne nomina quidem scire me volueris.

Slusij ipsissima verba⁴⁾ tibi describam quae sic habent.

Recentius exemplum curvae non bene cohaerentis mihi subministras, in tertia illarum, quas ingeniosi viri Mathematici Leidenses nobis propositas voluerunt; eam enim ex aequatione ipsa sine ulla alia operatione deprehendi, (quod et te animadversurum suspico) componi ex partibus curvae, cujus dimensio, tangens, centrum gravitatis, dudum ab alijs ostensa sunt. Itaque nolui πολυπραγμωνεῖν in re jam peracta, et ad primam me contuli, in qua tangentem duci posse ostendi hac methodo.

Detur punctum F tangendum, et applicata FD, ducatur per A eidem parallela



IAC, ductaque FC parallela AD, sumatur AH aequalis AG, et HI dupla CA. Tum fiant quatuor proportionales IC, HC, AC, BC.

Aio junctam BF tangere curvam in F. Ejusdem dimensionem geometricè inveni; habere nempe eam rationem ad parallelogrammum sibi circumscriptum, quam habeant inter se duo solida rationis notae. Sed quoniam res prolixa est, et eadem ratio continuo variat pro diversa longitudine axis, ut in Conoide hyperbolico et cylindro circumscripto accidit, contentus ero unico exemplo rem Arithmeticè declarare. Intelligatur applicata FD esse subtripla AG, aio parallelogrammum AF habere ad trilineum AFD eam rationem quam 64 ad 37. Ulte-

1) Voir la Lettre N^o. 424.

2) Voir la Lettre N^o. 430.

3) Ce furent J. Hudde et H. van Heuraet: voir la Lettre N^o. 434.

4) Voir la seconde moitié de la Lettre N^o. 430.

[p. 90]

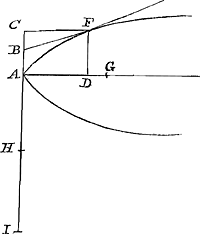
rius in hanc inquirere non vacavit, uti nec in secundam, longâ potestatum serie horridam: quam tamen arbitror detracta larvâ fore tractabiliorem: sed eam tibi relinquo, longiorem enim operam desiderare videtur quam ut ab homine varijs curis distracto explicari possit. In eo autem quod scribis te ijs Problematibus delectari in quibus inventio praecipua est, et calculus non difficilis planè tecum sentio; Ideoque tibi serio gratulor si quid non antea animadversum circa parabolam observasti. Gavisus sum interim Clarissimos viros ostendisse in quanam ratione curva mea secaretur à maxima applicatarum. Idem praestare potuissent in ea quae axem bifariam dividit et in alijs, quod nullo negotio animadvertes.

Haec ille. Ego verò accepto hoc ipsius responso, eadem inquirere caepi, cum hactenus avelli non potuissem ab incepto opere, scribendarum videlicet demonstrationum novi illius circa parabolam inventi, cujus Slusius mentionem facit.

Primae itaque lineae tangentem hoc modo ducendam invenio. Sit punctum in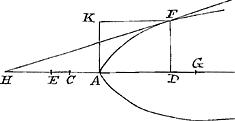



curva datum F. Et ordinatim applicetur FD productâque diametro GA, sint in continua proportione AG, FD, AC, CE⁵⁾ Et fiat AH dupla AE. dico rectam ab H per F ductam contingere curvam in F. Ad quadraturam vero quod attinet. dico completo parallelogrammo ADFK, positaque AG ∞ a, DF ∞ b, esse ▭ DK ad portionem comprehensam AFD ut a + b ad ½ a + ¾ b + 1/12 ab/a + b. Unde facile liquebit, rectè Slusium definivisse in illo casu suo rationem 64 ad 37. Centrum autem gravitatis quomodo in hac linea inveniri possit adhuc non video. Porro de tertia quoque rectè Slusius pronunciat esse eam ex curvae lineae, jam diu ante ab alijs expositae, partibus conflatam. Hoc enim et ipse perspexi haud difficulter. Tangens autem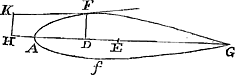



hujus lineae sic ducetur. Esto datum in curva punctum F, unde ordinatim applicetur FD. Interceptae vero DA sit triens utraque harum AH, HK; quarum AH sit in producta diametro sumta; HK vero ordinatim applicata. Dico ducta KF, eam tangere curvam in F.

Rectangulum porro, spatio AFGf aequale habebitur, sumtâ septima parte quadrati axis AG. Centrum denique gravitatis E ita dividit AG, ut GE sit ad EA sicut 19 ad 14.

At de secunda illa linea vestra neque mihi inquirere libuit, quam opinor haud

5) C'est-à-dire AG: FD = FD: AC = AC: CE.

[p. 91]

multò aliter ex segmentis alicujus simplicioris compactam esse. Neque verò difficile est eo modo obscuram atque intricatam reddere investigationem. Ejuscemodi vero problematis, quae prolixum calculum minantur neque egregiam prae se ferunt utilitatem, non libenter bonas horas impendo: Ideoque ea tantum mihi proponi velim quaerenda, quibus inventis operaepretium me facturum, atque aliquid scitu dignum consecuturum intelligam. Quanquam fateor non male me tempus collocasse,



dum hasce lineas ad examen revoco, siquidem ea occasione in aliam quandam deductus sum speculationem pulcherrimam, de qua alias pluribus. Caeterum id quod Slusius submonet posse ostendi secundum quam rationem curvae suae spatium dividatur ab ea quae axem bifariam dividit, et ab alijs; adeo verum experior, ut in universum, qualitercunque sectum fuerit⁵⁾ spatium curvae suae à recta linea, partium inter se ratio exhiberi queat.

Problemata Freniclij⁶⁾, non dubito ad te quoque ab autore missa esse: Quae cum aspicio, demiror sanè diversa hominum studia⁷⁾. Vale Vir Clarissime.

Hagae Com. 23 Nov. 1657.

Aen Mijn Heer Mijn Heer Fr. van Schooten, Professor der Mathematiquen inde Universiteyt Tot Leyden.

5) Dans la minute on lit:
secta fuerit axis, dicta partium ratio exhiberi possit.

6) Voir la Lettre N^o. 389.

7) Dans la minute on lit encore:
Caeterum ego demonstrationem Theorematis illius Fermatiani, Dato quovis numero non quadrato, dantur infiniti qui in datum numerum ducti, adscita unitate faciunt quadratum, pluris facerem quam reliqua omnia à Freniclio istis paginis tradita. Vale.