Oeuvres complètes. Tome II. Correspondance 1657-1659

N^o 430.
R.F. de Sluse à [Christiaan Huygens].
[novembre 1657.]¹⁾

La lettre se trouve à Leiden, coll. Huygens.
Elle est la réponse au No. 424 Chr. Huygens y répondit par le No. 433.

Nobilissime Domine

Ingeniosa prorsus est animaduersio Tua, quâ Cartesianarum regularum secundam quintae opponj demonstrastj: sed antequam ad explorandum nostrarum consensum accedam, pauca praefarj libet vt ὁμωνυμίαν in posterum excludam. In mobili (quod et Te facere arbitror) tria considero, molem, vim impressam (siue impetum, impulsum, momentum, motus gradum vocare mauis) et quae ab vtro-

1) La date doit tomber entre le 2 novembre et le 7 décembre.

[p. 87]

que pendet velocitatem. Molem Geometria metitur, Velocitatem per spatia aequali tempore decursa definimus, in impetus vero notitiam deducimur conferendo moles et velocitates; Quae enim mole inaequalia sunt, si impetu aequalj moueantur, velocitates habere nosti reciproce vt moles, ét si inaequalia sint impetusque pariter inaequales, velocitates sortirj, quarum ratio componitur ex ratione impulsuum et molium reciprocâ. Cum igitur mihi duo corpora in ratione triplâ proponis quae aequalj celeritate inuicem alliduntur, et minus ais duplo celerius quam aduenerat reflectj (ne haeream in ὁμωνυμίᾳ) explica, quaeso, num celeritatis nomine impetum vel potius velocitatem, vt videtur, intelligas; et interim scito ex meis regulis, vti et ex Tuis, sequi corpus minimum impactum in quantumlibet maius quiescens, illud mouere: et sj corpus minus impingat in maius quiescens quocumque impetu, (dummodo maius, minus, et eorum differentia sint in continuâ ἀναλογίᾳ) vtrumque post occursum eadem velocitate ferri in partes contrarias. Quod an ex Tuis etiam deducatur libenter intelligam. Quae de Patris Gregorij Parabolis scripsj, non reprehendendj studio a me dicta sunt, a quo ϕύσει ϰαὶ ἤϑει alienissimum me profiteri audeo, sed ἐλευϑερίᾳ ϕιλοσοϕιϰῇ, ὅτι χρὴ προτιμᾷν την ἀλήϑειαν. Credidj autem licuisse mihj primam eius curuam iuxta eius definitionem²⁾, fretus Juris-consultorum axiomate quod exempla declarent non restringant. Sed vt res clarior euadat, si tantj est, considera quadratum PB, in quo parabola ARC,



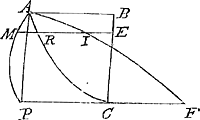cuius vertex C applicata AB, Tum ductâ qualibet aliâ RE, intellige ab ipsâ (productâ si opus sit)resecari RI, ita ut eadem sit ratio quadratj PC ad quadratum RI, quae CB ad BE, ipsique IR sumj in directum aequalem RM, et hoc semper fierj donec per puncta PMAIF duci possit curua. Hanc vtique esse parabolam virtualem constabit ex earum definitione, quam assignat Autor paginâ, vt annotauj, 840; et tamen ex partibus curuarum male cohaerentibus compingj vel sine calculo deprehendes. Quod autem dixj ostendisse me, primam esse ad parallelogrammum sibj circumscriptum in ratione subsesquialterâ, ita intellexj non quasj ex hac Patris Gregorij compositione deprehendissem, id enim facile et obuium est, sed quod ante visas eiusdem contemplationes, id ex ipsâ aequatione deduxissem. ἀλλὰ τούτων μὲν ἅλις, ὡς τῆς δρυός. Recentius exemplum curuae non bene cohaerentis mihj subministras, in tertiâ illarum, quas ingeniosi virj Mathematicj Leydenses nobis propositas voluerunt; eam enim ex aequatione ipsâ sine vllâ aliâ operatione deprehendj, (quod et Te animaduersurum scio) componj ex partibus curuae, cuius dimensio, tangens, centrum grauitatis, dudum ab alijs ostensa sunt. Itaque noluj πολυπραγμωνεῖν in re iam peractâ, et ad primam me contuli, in quâ tangentem ducj posse ostendj, hac methodo.

2) Il semble qu'un mot manque ici.

[p. 88]

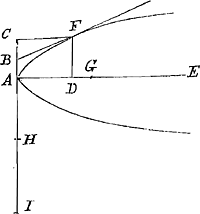Detur punctum F tangendum, et applicatâ FD ducatur per A eidem parallela IAC, ductaque FC parallelâ AD, sumatur AH aequalis AG et HI dupla CA. Tum fiant quatuor proportionales IC, HC, AC, BC, aio iunctam FB tangere curuam in F. Eiusdem dimensionem Geometricé inueni, habere nempe eam rationem ad parallelogrammum sibj circumscriptum, quam habeant inter se duo solida rationis notae. Sed quoniam res prolixa est, et eadem ratio continuo variat pro diuersâ longitudine axis, vt in Conoide Hyperbolico et cylindro circumscripto accidit, contentus ero vnico exemplo rem Arithmetice declarare.

Intelligatur applicata FD esse subtripla AG, aio parallelogrammum AF habere ad trilineum AFD eam rationem quam 64 ad 37.

Vlterius in hanc inquirere non vacauit, vtj nec in secundam longâ potestatum serie horridam; quam tamen arbitror detractâ laruâ fore tractabiliorem; sed eam Tibj relinquo, longiorem enim operam desiderare videtur quam vt ab homine varijs curis distracto explicarj possit. In eo autem quod scribis Te ijs Problematibus delectarj in quibus inuentio praecipua est, et calculus non difficilis, plané Tecum sentio; Ideoque Tibj serio gratulor si quid non antea animaduersum circa parabolam obseruastj. Gauisus sum interim Clarissimos Viros ostendisse in quanam ratione curua mea secaretur a maximâ applicatarum. Idem praestare potuissent in eâ quae axem bifariam diuidit et in alijs, quod nullo negotio animaduertes. Pene oblitus eram monere, me in Epigrammate Graeco πέντε τομὰς intelligere eodem modo quo in sectionibus conicis. Ita ut hic tres dent spiricas nouas, at reliquarum duarum vna per axem spiram exhibeat, alia huic normalis vel circulum vel corollam. Quo autem suo merito spiricae tantum Persei applausum mereantur, nescire me fateor, nisj ab eo affectu oriatur quo in res a nobis inventas ferri solemus. Hoc interim mirarj contigit quod mihj in earum descriptione Theonem cites, cum ego Te ad Proclum remiserim, qui prolixo in j^mo. Euclidis volumine multa veterum inuenta libauit. Clarissimi Freniclij numeris non afficior.

Defuit me charta, at non voluntas testandj Tibj quam sim

Ex animo Tui obseruantissimus Renatus Franciscus Slusius.