Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 690]

N^o 2881.
B. Renau à Christiaan Huygens.
[octobre ou novembre 1694].

La pièce¹⁾ est la réponse au No. 2869.
Chr. Huygens y répondit par le No. 2882.

Reponse de M. Renau.

Il paroist que M. Huguens n'est pas content des raisons que je rapporte dans ma Réponse²⁾ aux objections³⁾ qu'il a faites à mon Traité de la Theorie de la Manoeuvre des Vaisseaux⁴⁾, & que la maniere assurée dont un homme de sa reputation replique⁵⁾ à ma Réponse, donne occasion aux personnes mesme verées dans les Mathematiques, de se laisser prévenir en sa faveur; j'espere les détromper entierement, s'ils veulent se donner la peine de suivre mon raisonnement sans prévention; & pour cela, je ne m'attacheray qu'à ce qui a donné occasion à M. Huguens de tomber luy-mese dans l'erreur.

M. Huguens dit⁶⁾: Pour sçavoir qui



de nous deux a raison, imaginons-nous...& il conclud. Donc aussi la force avec laquelle le vent pousse le vaisseau selon BG, est à la force dont il est pousse selon BK, comme BG à BK, et non pas comme les quarrez de ces lignes comme veut M. Renau.

Je ne conviens point du tout que cette derniere consequence soit bien tirée, ny de beaucoup d'autres choses qui sont dans ce raisonnement, parce qu'il me paroist que M. Huguens confond à tous momens les puissances ou les forces, avec les poids ou les masses, & qu'il ne fait point d'attention aux vitesses des corps pour sçavoir leurs puissan-

1) Elle constitue la seconde partie de l'ouvrage: ‘Replique de M. Huguens à la réponse de M. Renau, Capitaine de Vaisseau, & Chevalier de l'Ordre de S. Loüis, sur le principe de la Theorie de la Manoeuvre des Vaisseaux et la réponse de M. Renau a la Replique de M. Huguens. A Paris Chez Estienne Michallet, premier Imprimeur du Roy, ruë S. Jacques, à l'Image S. Paul. M.DC.XCIV. De l'exprès Commandement de Sa Majesté’. In-8^o de 2 feuilles, chacune de 8 pages (19 p.).
La première partie, qui occupe les pages 3-11 de l'ouvrage, reproduit textuellement notre pièce N^o. 2869, sous l'en-tête: ‘Replique de M. Huguens à la réponse de M. Renau, Ingénieur General de la Marine en France. Extraite de l'Histoire des Ouvrages des Sçavans du mois d'Avril 1694 à l'article V’.
C'est à l'obligeance de M. Delisle, administrateur de la Bibliothèque Nationale à Paris, que nous devons la connaissance de cette seconde réponse de Renau, dont l'existence, comme aussi celle de la nouvelle réplique de Huygens, notre N^o. 2882, semble avoir échappé à 's Gravesande; il ne les a pas reproduites dans les ‘Opera Varia’ avec les autres pièces qui se rapportent à la polémique Huygens-Renau.

2) Voir la pièce N^o. 2848.

3) Voir la pièce N^o. 2826.

4) L'ouvrage cité dans la Lettre N^o. 2813, note 17.

5) Dans la pièce N^o. 2869.

6) Voir, pour les passages cités, la page 656 de la pièce N^o. 2869.

[p. 691]

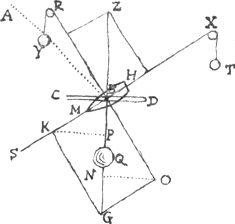
ces, ce qui me fait douter de sa pretenduë demonstration, malgré l'opinion que j'ay de son sçavoir, & l'assurance qu'il donne de la certitude de ses regles de Mechanique, qu'il dit estre établis dés longtemps, & dont il ne croit pas que j'ose disconvenir.

Quoy qu'il en soit, comme toute nôtre dispute est reduite à sçavoir si la force que le poids Q fait selon BG⁷⁾, est à la force que le mesme poids fait selon BK, comme la ligne BG est à la ligne BK, ainsi que M. Huguens le pretend, ou bien comme le carré de BG est au quarré de BK comme je le pretend, j'essayeray encore de convaincre Monsieur Huguens.

Mais pour éviter les équivoques, je diray qu'un petit corps a la mesme puissance qu'un grand, lorsque la vitesse du petit est à celle du grand, comme le grand corps est au petit; ce qui fait qu'un petit corps est en équilibre avec un grand, lorsque par le moyen d'une machine ou de cordes, l'un ne sçauroit se mouvoir sans faire mouvoir l'autre, en telle sorte que la vitesse de l'un soit à la vitesse de l'autre, en raison reciproque de leurs masses, c'est-à-dire que le produit de la masse de l'un par sa vitesse, soit égal au produit aussi de la masse de l'autre par sa vitesse.

Je dis de plus que comme le point R est supposé infiniment éloigné de B, toutes les lignes tirées du point R sur la ligne BK sont toutes égales, & font des angles droits avec la ligne BK, aussi bien que celles tirées du mesme point R sur la ligne OG, c'est-à-dire que RB est égale à RK, & que l'angle RKB est égal à l'angle droit RBX, & la ligne RO égale à la ligne RG, enfin que l'angle RGO, est droit.

De mesme imaginant le point X à l'infini, XB est égale à XO, & XK à XG, & les angles XOB & XGK sont droits⁸⁾.

Presentement imaginons-nous que la ligne BG exprime la grandeur du poids

7) La figure du texte a été calquée sur celle de l'ouvrage original.

8) On trouve encore imprimé en marge: ‘Il faut icy imaginer les lignes tirées RK, KG: XO, XG’.

[p. 692]

Q, & qu'il y ait une poulie en X par dessus laquelle passe la corde BX, à laquelle tienne un poids T de la grandeur de BK. Si la corde BR est attachée en R, je dis que le poids T est en équilibre avec le poids Q, c'est-à-dire que la puissance du poids Q selon BK, est égal à la puissance du poids T, par la raison que le point B ne peut venir par exemple au point K, sans que le poids T ne monte de la quantité BK, & alors le poids Q descend de la quantité BP. Donc par la disposition de ces cordes le poids Q ne peut pas descendre sans faire monter le poids T, en telle sorte que la vitesse du poids Q en descendant, ne soit à la vitesse du poids T en montant, comme BP est à BK; Mais à cause des triangles semblables, BP est à BK, comme BK est à BG: Donc la vitesse du poids Q en descendant, est à la vitesse du poids T en monrant [sic], comme le poids T est au poids Q; & par consequent le rectangle de BG & de BP qui represente la puissance du poids Q, parce que c'est le produit de sa vitesse par sa masse, est égal au quarré de BK, qui represente la puissance du poids T, à cause que c'est aussi le produit de la vitesse du poids T par sa masse; & ces deux puissances estant égales, ces deux poids sont en équilibre, & par consequent le quarré de BK exprimera la puissance du poids Q selon BK.

De mesme le point X estant fixe, si l'on suppose une poulie en R comme on en a supposé une en X, & qu'on suspende à la corde BR prolongée un poids Y, de la grandeur BO, ce poids sera en équilibre, avec le poids Q, & en faisant le mesme raisonnement que pour le poids T, on verra que la puissance du poids Q selon BO, sera exprimée par le quarré de BO.

D'où il s'ensuit que la puissance du poids Q selon BK, est à la puissance du mesme poids selon BO, comme le quarré de BK est au quarré de BO, & non pas comme BK est à BO, comme il suit du principe de M. Huguens.

Soit encore consideré le poids Q suspendu en B, le poids Y en R, & le poids T en X, je dis que je poids Q sera en équilibre avec ces deux poids; Parce que le point B ne peut venir par exemple au point G, sans que le poids T ne monte de la quantité BK, & le poids Y de la quantité BO, comme il se voit par ce que j'ay dit cy-devant, & alors le poids Q descend de la quantité BG; Donc par la disposition de ces cordes, le poids Q ne peut pas descendre sans faire monter ces deux poids, en telle sorte que la vitesse du poids Q en descendant, ne soit à la vitesse du poids T en montant, comme BG est à BK, & à la vitesse du poids Y, comme BG est à BO, & alors la puissance du poids Q selon BG, est exprimée par le quarré de BG, parce que c'est le produit de la vitesse du poids Q par sa masse; & par la mesme raison le quarré de BK exprime la puissance du poids T, & le quarré de BO, celle du poids Y: & comme ces deux quarrez sont égaux au quarré de BG, la puissance du poids Q selon BG, est égale aux deux puissances des deux autres poids, & par consequent le poids Q est en équilibre avec les deux autres poids.

D'où il suit que la puissance du poids Q selon BG, est à la puissance du poids T, comme le quarré de BG est au quarré de BK, & a la puissance du poids Y, comme le quarré de BG est au quarré de BO.

[p. 693]

Mais on a fait voir cy-devant que la puissance du poids Q selon BK, estoit égale à la puissance du poids T, & selon BO, à la puissance du poids Y, donc la puissance du poids Q selon BG, est à la puissance du mesme poids selon BK, comme le quarré de BG est au quarré de BK, & non pas comme BG est à BK, comme le pretend M. Huguens, & a la puissance selon BO, comme le quarré de BG est au quarré de BO.

D'où l'on voit que si le Vaisseau HM a sa quille dirigée selon HBM, & sa voile CBD, perpendiculaire sur BG, le vent AB le pousse selon BG & selon BK, comme fait le poids Q, si la corde BR censée infiniment longue, & attachée en R, fait que le Vaisseau ne puisse se mouvoir que le long de BK: on voit dis-je que le Vaisseau ira de B en K en mesme temps quil auroit esté en G, s'il fendoit l'eau également de tous costez, & non pas en S, comme veut M. Huguens⁹⁾.

Ensuite M. Huguens pour indiquer en peu de mots ce qui a pû donner occasion à mon erreur¹⁰⁾ pretenduë, continuë de cette sorte¹¹⁾. Je diray seulement que l'origine de l'erreur....

Je ne comprens pas comment M. Huguens cite cet endroit comme l'origine de mon erreur: car puisque selon luy, en suppléant le mot d'égales, la démonstration & ce qu'elle conclut, sont comme il faut: il s'ensuit seulement qu'il s'exprime dans cet endroit un peu plus exactement que moy; ce qui au fond n'est point une faute, d'autant plus que par ma démonstration, ni dans les consequences que j'en ay tirées, on ne peut pas entendre la chose autrement: & en cela, j'ay suivi un usage assez ordinaire aux Geometres qui se servent du mot de ligne, pour specifier une ligne droite, lors qu'il n'y a point danger d'équivoque.

J'espere que ce que je viens de faire voir à M. Huguens suffira pour luy prouver, & aux personnes versées dans les Mathematiques qu'il cite¹²⁾, que ce qu'ils croyoient une erreur capitale dans mon Traité de la Manoeuvre des Vaisseaux, n'est point une erreur, & que je ne raisonne pas tout-à-fait si mal qu'il dit à la fin de sa replique, quoy-que je ne fasse pas profession de Mathematiques. Et je puis assurer M. Huguens, que si ce que je prens la liberté de luy avancer ne me paroissoit pas tres-évident, je l'abandonnerois sans peine, & je l'avouërois publiquement, en me condamnant moy-mesme, comme j'ay fait dans ce qui regarde la position du Gouvernail, quoy-qu'il me fist l'honneur de m'approuver dans cet endroit.

FIN.

9) Consultez, sur la construction du point S, la page 655 de la pièce N^o. 2869.

10) Comparez le second alinéa de la page 655.

11) voir la page 657 de la pièce N^o. 2869.

12) Voir la page 655.