Oeuvres complètes. Tome VI. Correspondance 1666-1669

N^o 1736.
F.W. de Nulandt à Christiaan Huygens.
23 mai 1669.

La lettre se trouve à Leiden, coll. Huygens.
Elle est la réponse au No. 1728.

A la Haije le 23 de Maij 1669.

Monsieur,

Vn voijage, que ie fus oblige de faire en Zelande m'a empesche de pouuoir respondre plustost a la vostre, par la quelle ie suis aise d'apprendre, que mon calcul¹⁾

1) Consultez la pièce N^o. 1706. Notre pièce N^o. 1728, que nous avons empruntée aux ‘Elementa physica’ de Nulandt, ne contenait pas cette partie de la lettre de Chr. Huygens.

[p. 435]

ne contient aucun paralogisme; mais quant a vostre Methode puisque elle est plus facile, sans estre oblige de se seruir des Tables de Sinus ie l'estime fort et en cas que vous soijez resolus d'en faire part quelque jour au public, i'oseraij vous prier de me la vouloir communiquer; de quoij ie vous seraij infiniment oblige.

Touchant ce que vous me demandez de la nature du l'infini & du centre esgal a sa peripherie; J'aij remarquè que l'infini & le rien a peine peuuent ils estre conçeus l'un sans l'autre, car ce qui est infini a l'esgard de quelque chose, cette mesme chose est rien a l'esgard de l'autre, de sorte que rien a la mesme proportion a quelque chose finie, que cette mesme chose a l'infini; D'ou suit qu'une chose finie est la moijenne proportionelle entre le rien & l'infini;

J'aij remarque de mesme que ces noms sont aequiuoques & relatifs & que la mesme chose peut estre infinie a l'esgard d'une, & rien a l'esgard de quelque autre chose, comme vne ligne donnè est infinie a l'esgard d'un poinct & toutesfois est rien a l'esgard d'une surface; De mesme vne chose peut estre infiniment plus grande que vne autre chose a l'un esgard, & luy estre esgale a vn autre esgard. Ce qui n'aijant pas este considere par le Pere Bettin²⁾ & quelques autres Geometres, a cause tant de conuulsions dans leurs testes touchant le Paradoxe³⁾

2) Mario Bettini naquit le 6 février 1582 à Bologne, où il mourut le 7 novembre 1657. Il entra chez les Jésuites en 1595, et professa à Parme les mathématiques, puis la philosophie. Il publia divers écrits, entre autres:
Apiaria vniversae Philosophiae Mathematicae, in qvibvs Paradoxa, Et nona pleraque Machinamenta ad vsus eximios traducta, et Facillimis demonstrationibus confirmata. Opvs Non modo Philosophis Mathematicis, sed & Physicis, Anatomicis, Militaribus viris, Machinariae, Musicae, Poëticae, Agrariae, Architecturae, Mercaturae professoribus, &c. vtilissimum: Curiosissimis inuentis refertum, sigurarum aeris formis cusarum numerosa, & speciosa varietate ornatum, & in duos Tomos distributum; Vna cum gemino copiosissimo Indice, altero propositionum, altero rerum. Accessit ad sinem secvndi Tomi Evclides Applicatvs. Et conditus ex Apiariis, indicatis vsibus eximijs praecipuarum propositionum in prioribus sex libris Euclideorum Elementorum. Accessere et Analectà &c. Avthore Mario Bettino Bononiensi e Soc. Jesv. olim in publico Parmensi Gymnasio Philosophiae Mathematicae, & Philosophiae Moralis Lectore. Bononiae. Typis Jo. Baptistae Ferronii cum facultate Superiorum. Anno salutis m.dc.lxv. II. Tomes in-folio.
De cet ouvrage parut plus tard la suite:
Apiariorvm Philosophiae Mathematicae, Tomvs Tertivs Complectens Fvcaria, et Avctaria Militaria, Stereometrica, Conica, et novas alias ivcvndas praxes ac theorias in omni Mathematicarvm Scientiarvm Genere. Accessit Appendix hvivs Tertii Tomi Pars Praecipua, In qua sunt Defensiones contra Oppositiones Noualmagesti: ope, ac opera Aqvilonariis Academiae. Bononiae, m.dc.lvi. Sumptibus Sebast. Combi & Ioan: La Noù, cvm Facvltate Syperiorvm. in-folio.
Ce dernier volume contient le passage cité, dans la sectiou Auctaria ad Apiarii III, § 1, N^o. III, pag. 62.

3) Consultez dans les ‘Discorsi e demonstrazioni matematiche’ [voir la Lettre N^o. 17, note 1], page 29, (Albèri, Le opere di Galileo Galilei T. 13, p. 32) la démonstration se terminant par ces mots: par dunque che la circonferenza di un cerchio immenso possa chiamarsi eguale a un sol punto.

[p. 436]

de Galilee ou il montre qu'un centre peut estre esgal a sa peripherie; car ils n'auroijent jamais trouuè de difficulte s'ils auoijent considere que dans ces corps dont il est question les arces des cercles & des anneaux, sont esgales, & non les periferies, plutost au contraire, tant plus que les sections s'aprochent du bout du Cone tant plus grande proportion il ij a entre les perimetres de l'un de de l'autre. c'est pourquoij il ne se fault pas estonner que quoij que la periferie du cercle soit infininement plus grand en longueur que le point, neantmoins il luij soit esgal quant a la capacite puisque elle est rien aussi bien que la capacite de la periferie du cercle; De mesme tout le cercle peut estre esgal a vn point a l'esgard de la solidite puisque nij l'un nij l'autre n'ont poinct; Et ie suis bien estonnez qu'une chose si facile ait pu fournir matiere de dispute entre gens d'esprit; Mais ie ne sçaij pas si ie m'explique assez & s'il ne m'arriue ce que jadis a dit le Poete⁴⁾;

Dum breuis esse laboro

Obscurus fio.

Mais scachant qu'a vn bon entendeur ne faut qu'une demi parole, puisque i'escris a uous; il ne m'est pas necessaire d'emploijer plus de paroles.

Quant aux regles de la percussion lesquelles vous dites auoir donnez au public dans le journal de sçauans⁵⁾, i'auraij eu vn grand plaisir de les voir, mais jusques asteur ie n'aij pas pu auoir cette satisfaction, Et nous sommes si malheureux icij, que nous n'auons iamais part aux belles choses lesquelles se publient ailleurs si non lors qu'elles sont vielles; Mais ie vous enuoyeraij puisque vous le voulez vne partie des miennes, a fin que vous puissiez juger si elles s'accordent auecq les vostres; Je me contenteraij de copier les propositions, puisque nij le temps nij le papier souffre les Demonstrations⁶⁾.

Voila vne partie de mes regles desquelles vous pourrez juger si nous sommes d'accord, & ie vous supplie treshumblement, de me le vouloir faire sçauoir.

Je m'estonne que uous trouuez paradoxe ce que i'aij escrit touchant le mouuement circulaire & la tendence du Centre & que uous demandez l'experience au lieu de demonstration. Cependant il est aise a comprendre qu'il nij a aucune connexion entre le mouuement Circulaire d'un canal, et le mouuement d'une boule laquelle est dedans; Mesme le mouuement Circulaire du Canal est causee par accidens seulement, puisque l'un de ses bouts estant attache par la est empeschè de poursuiure son mouuement en ligne droite & oblige de tourner sur ce bout comme sur vn centre circulairement; De la façon qu'on ne troue point du mouuement circulaire dans tout l'Vniuers si ce n'est per accidens, lors que les corps estans empeschez de poursuiure leur mouuement en droiture sont obligez de se courber obliquement; la Verite de ce principe aijant este reconnu par Monsieur Des Cartes dans

4) Horatius, Ars Poetica, vs. 25, 26.

5) Voir la pièce N^o. 1716.

6) Voir la pièce N^o. 1737.

[p. 437]

la seconde partie pour une loij de nature, ie m'estonne qu'il l'a oublie dans sa Troisiesme partie⁷⁾; Mais il nij auoit autre moijen d'establir cette belle Chimere des Vortices Celestes, Et l'analogie luij parut trop belle pour l'abondonner⁸⁾.

Mais enfin pour monstrer ce que i'aij auancee que c'est la figure du canal laquelle est cause, quand on le tourne Circulairement que la boule contenuë s'esloigne toujours du centre. Je dis hardiment mesme sans auoir fait l'experience que si le coste du Canal n'est pas le diametre du Cercle du mouuement, il se peut faire que la boule s'aproche du centre aussi bien, que s'eloigne. par exemple soit le canal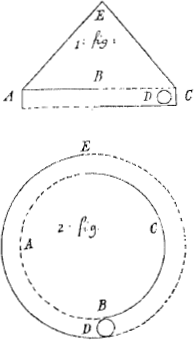



ABC, la boule D, le centre du mouuement in E, ie dis quand le Triangle EAC sera tourne sur le centre E selon la ligne ABC que la boule D a la fin sortira par A c'est a dire priemierement elle s'approchira du centre jusques in B & puis derechef s'eloignera.

Mais quand la Canal est Circulaire comme on voit dans la 2. figure & que le centre du mouuement soit in E, la boule D faira tout le tour. Mais selon que le centre du mouuement sera pose hors ou dans le cercle le mouuement de la boule aura des autres simptomes.

Mais quand le canal seroit vne spirale pose le centre du mouuement estre le mesme que le centre de la spirale, vne boule tourne dedans d'un coste approchera auec rapidite du centre, & il demeurera, mais quand on le tournera de l'autre coste elle s'eloignera dercchef;

Je n'adjouste point les demonstrations, puisque ie ne doubte nullement que uous ne les trouiez vous mesme apres auoir quitte le preiuge que vous auez encore, puisque elles sont assez faciles.

Pour le reste puisque il ij a apparence que cette este ie pourrois faire vn voijage, aux Ifles de l'Amerique, ie vous supplie de me faire sçauoir si en ces quartiers la ie serois capable de rendre quelque seruice ou a vous ou a la republique des Sçauans; J'aij dessein de mener auecq moij deux Horloges a pendule vn de vostre façon & l'autre de la mienne, ou le pendule n'est pas attache a vn filet comme vous faites parce que cela ne laisse pas d'auoir ses incommoditez, & ie n'aij pas besoing non plus de la description de la roulette pour esgaler les vibrations, car elle est rarement fait auec exactitude par les Ouriers; De sorte que ie les esprouueraij

7) Il s'agit ici des ‘Principia Philosophiae’ de R. des Cartes.

8) Lisez: abandonner.

[p. 438]

touts deux; Si ie auois les Ephemerides des Satellites de Jupiter ie tascheraij aussi de marquer les longitudes par ce moijen; Cependant en quel quartier du monde que ie puisse estre, ie seraij toujours auec passion

Monsieur

Vostre tres humble et tres obeissant Seruiteur

F.W. Baron de Nulandt.