rectae FB refringatur in I, ductaque Tangente GD, erit recta FDK ipsi ad angulos rectos, si iam detur refractionem vitri ad aerem esse vt lineam M ad lineam L datas,
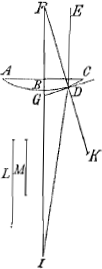
erit iuxta Cartesium vt M ad L ita sinus anguli FDE ad Sinum anguli IDK, dato ergo angulo FDE datur & angulus IDK sed angulus FDE propter paralelismum linearum FB, ED aequatur angulo BFD, qui mensuratur per arcum BD assumptum quare tam angulus FDE quam angulus refractus IDK sunt cogniti; quare & illarum complementa FGD, GDI cognita erunt. Sed angulus FGD externus cum sit aequatur duobus GDI complemento anguli refracti, & GID erit ergo angulus GID excessus quo complementum anguli refracti superatur a Complemento anguli arcus assumpti, quare cum eadem sit differentia inter angulos, quae est inter illorum complementa, erit quoque angulus GID differentia inter angulum arcus assumpti & angulum refractum; in Triangulo ergo FID noti sunt omnes anguli vna cum latere FD radio nempe Sphaerae datae, quare erit iuxta doctrinam Triangulorum ut Sinus anguli FID differentia inter angulum datum & refractum ad rectam FD radium Sphaerae datae ita Sinus anguli FDI aequalis Sinui anguli refracti IDK ad rectam FI a qua ablata recta FB aequali radio dato reliqua erit BI longitudo foci.
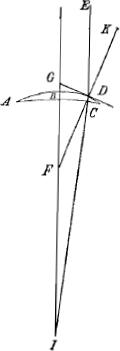
Verum si radius ED ex aere refringatur in vitrum ABC & progrediatur in I, factis omnibus vt supra patet angulum EDK aequari angulo BFD qui assumitur, datus est ergo, cum itaque sit iuxta Cartesium vt linea L ad lineam M. ita Sinus anguli EDK ad Sinum anguli FDI refractum, si lineae L & M sint datae, datus erit et angulus refractus FDI, patet itaque cum angulus BFD assumptus, sit externus, angulum FID esse differentiam inter angulum BFD assumptum, & FDI refractum. In Triangulo ergo FDI dantur omnes anguli, cum latere FD, erit ergo vt Sinus anguli differentiae inter angulum assumptum & refractum ipsi competentem, ad radium Sphaerae datae ita Sinus anguli assumpti, ad rectam quandam cui si addatur radius datus, componetur tota longitudo foci.