Oeuvres complètes. Tome X. Correspondance 1691-1695

[p. 79]

N^o 2674.
A. de Graaff à Christiaan Huygens.
17 avril 1691.

La lettre se trouve à Leiden, coll. Huygens.
Elle est la réponse au No. 2670.
Chr. Huygens y répondit par le No. 2679.

Mijn Heer

17 April 1691.

Sende VE hier nevens het kasie, het Loot, 2 pennen en de strik, zoude het eerder gesonden hebben, maar ben seer belemmert geweest met de Exames der Stierlieden, het welk ook oorsaak is geweest dat ik VE Tractatiens, mij laast gesonden, maar even heb ingesien: ik bedank daarvoor VE hartelijk: bij occasie sal ik hen, en voornamelijk het laatste, wat naukeuriger nazien: maar het is beschreven in een taal waarvan ik gansch onkundig ben; en t'en ware het de Mathesis raakte, ik zoud er geheel niets uit konnen verstaan.

Ik hebbe niet de minste tijding van mijn zoon, noch en verwacht ze ook niet als met de Retourvloot.

Ik zie dat VE memory niet onfeylbaar is, of ik moeste VE qualijk onderricht hebben, dat ik niet kan geloven. 't is niet deze eygenschap waarin Thirnhaus geabuseert is, die VE mij voordraagt, welke ik mede goet bevonden hebbe, maar de eerste, waarin hij wil dat altijt HD ∞ DK zal wezen¹⁾.

Mijne calculatie heeft mij gegeven de volgende getallen

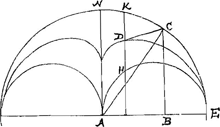
als EC is 90.0 ≫ DK 50000 en DH 50000, diff: 0

85.0 ≫ DK 49432 en DH 48000, diff: 1432

80.0 ≫ DK 47789 en DH 44990, diff: 2799

70.0 ≫ DK 41943 en DH 38379, diff: 3564

60.0 ≫ DK 34263 en DH 31880, diff: 2383

50.0 ≫ DK 26456 en DH 25789, diff: 667

45.0 ≫ DK 22830 en DH 22904, diff: 74

40.0 ≫ DK 19466 en DH 20115, diff: 649

30.0 ≫ DK 13534 en DH 14788, diff: 1254

20.0 ≫ DK 8509 en DH 7918, diff: 1209

10.0 ≫ DK 4098 en DH 4820, diff: 722

5.0 ≫ DK 2030 en DH 2405, diff: 375

0.0 ≫ DK 0 en DH 0, diff: 0

Waar uyt blijkt het merkelijk verschil met het geene Thirnhaus daarvan affir-

1) Consultez, sur cette erreur de von Tschirnhaus, la pièce N^o. 2626.

[p. 80]

meert. daar zoude wel eenige misrekening in konnen wezen, alzoo ik het zelfde alleen, en dat maar eens, uytgerekent hebbe: doch het kan niet merkelijk wezen. Ik hebbe ook vaak instuytstraalen getrokken, in een groote en net verdeelde Cirkel, die ik gedrukt hadde, en daarin quam het oogschijnlijk overeen met de voornoemde getallen.

En zoo ik 't wel onthouden hebbe; de autheur gaat deze eygenschap ook voorbij in de Acta van Lypzig²⁾, alwaar hij nochtans de andere aantekent en bewijst³⁾.

Ik hadde het abuys aan Monsr. Macreel⁴⁾ gecommuniceert, welke zeyde met hem te corresponderen, en ik vertrouwe dat die hem daarvan kennisse zal gegeven hebben.

Ik hebbe voor omtrent 2 jaren eens nagespeurt zijn Regel op de Quadrature der kromlinische figuren⁵⁾: doch kon der niet door komen, omdat ik niet kon vinden de getallen die hij voegt bij i, k, en l.

hij stelt i ∞ ca+2dx

k ∞ 2eaa+3fax+4gxx

l ∞ 3ha^3+4iaax+5kaxx+6lx^3

naar mijn gissing moesten der andere getallen bijstaan kleender als deze doch omdat de geheele zaak mij duyster bleef, zoo geloof ik dat ik hem niet wel zal gevat hebben: hierom, zoo VE mij dies aangaande eenige onderrichting kon geven, het zoude mij aangenaam zijn.

Zijn Regel op de Tangenten⁶⁾ heb ik gevonden en zijn methode op de wegneming der tussentermen⁷⁾ scheen mij toe dat ik zoude hebben konnen magtig werden; doch ben niet tot de uytrekening gekomen.

Ik hebbe de Hr. Bloquery laten lezen hetgeene UE wegens de horologymaker schrijft: zijn E. geliefde te antwoorden dat aan de Hr. van Dam, in den haag zijnde, zoude geschreven werden om de Rekening te betalen.

Afkortende, verblijve, naar cordiale groeten,

Mijn Heer

Sijn ootmoed.^en Dienaar Abraham de Graaff.

Amsterdam den 17 April 1691.

2) L'article de 1690, cité dans la note 15 de la pièce N^o. 2626, et dans lequel von Tschirnhaus reconnaissant l'erreur commise dans l'article de 1682 remplace sa fausse construction de la catacaustique par la véritable, que probablement il avait empruntée au ‘Traité de la Lumière’ de Huygens.

3) Comparez la page 72 de l'article de 1690, où ce théorème est mentionné, mais sans démonstration.

4) Dirck Makreel; voir la Lettre N^o. 2485, note 3.

5) L'article de von Tschirnhaus, cité dans la note 10 de la lettre 2274.

6) Voir la Lettre N^o. 2274, note 8.

7) Voir la Lettre N^o. 2274, note 11.