Oeuvres complètes. Tome IX. Correspondance 1685-1690

[p. 198]

N^o 2477.
Christiaan Huygens à H. Coets.
27 août 1687.

La minute et la copie se trouvent à Leiden, coll. Huygens.
La lettre est la réponse au No. 2474.

Sommaire:	A Mr. Henr. Coets. Sa methode^1) est bonne pour representer a l'oeil la figure de ces courbes. Elle seroit plus considerable si elle pouvoit servir aussi dans des courbes dont l'Equation consiste en plusieurs termes.
	Mais je ne croy pas qu'elle y aille bien loin, parce que dans ces sortes l'une des inconnues x,y peut avoir plusieurs valeurs.
	Mr. des Cartes lettre 5e du 3 vol. donne a entendre qu'il faut une equation cubique pour trouver tous les points de cette courbe qu'on nommoit le galand^2).
	L'on ne peut pas dire que vostre maniere de trouver les points des courbes ne soit geometrique ni qu'elles ne soient geometriques au sens de M. des Cartes mais l'on n'avoue pas pour cela que vous ayez une methode geometrique de decrire ces courbes ni qu'estant decrites ainsi par des points elles puissent servir a la construction geometrique des problemes. Car a cela selon moy il n'y a point de courbe qui puisse servir si non celles qu'on peut decrire entieres par le moyen de quelque machine ainsi que le cercle par le compas et les sections coniques par les instruments qu'on a inventez pour cela. Car les courbes decrites a la main et menees par des points ne donnent que des solutions approchantes, et qui ne se peuvent pas dire parfaites ni par consequent geometriques^3).

Hage den 27 Aug. 1687.

Mr. H. Coets tot Arnhem.

Mijn Heer

Ick ben tot nu toe belet geworden, soo door indispositie als daer nae door eenighe andere occupatien van UE antwoordt te laeten toekomen op sijn schrij-

1) Il nous semble évident qu'il s'agit d'une méthode pour obtenir des représentations paramétriques des coordonnées des points d'une courbe algébrique donnée, permettant de construire avec la règle et le compas autant de ces points qu'on voudra.
Outre l'exemple communiqué dans le texte de la lettre, on en rencontre encore un autre dans le livre F des Adversaria, p. 280 avec la suscription: Ex probl. 10^o Coetsij. Cette fois il s'agit de la courbe q⁶x³ = q²ry⁶ - ry⁸, dont l'équation est remplacée par les deux suivantes: y² = bx; x = -q⁶ + qqrb³ / rb⁴ (b paramètre).

2) Allusion au passage suivant de cette lettre, adressée à Mersenne et datée du 23 août 1638: ‘Au reste puisque je voy qu'il (Roberval) a pris plaisir à considérer la figure de cette ligne’ (celle dont l'équation s'exprime par x³ + y³ - xyn = o) ‘laquelle il nomme un Galand ou une fleur de jasmin, je luy en veux donner une autre qui ne mérite pas moins que celle là les mesmes noms et qui est néanmoins beaucoup plus aisée à descrire, en ce que l'invention de tous ces points ne dépend d'aucune équation cubique’. Remarquons d'ailleurs que la courbe citée, puisqu'elle est unicursale, se laisse très bien construire point par point sans résoudre une équation cubique. On pourrait poser par exemple: x = n³k / n³ + k³, ny = kx (k paramètre).

3) Ce sommaire se trouve inscrit dans le Livre F des Adversaria, p. 279.

[p. 199]

vens van den 20 Julij. Ick sende dan UE sijn Tractaet van het beschrijven der kromme linien wederom, en wat aengaet die van de Equatie a¹⁴y³ ℞ x¹⁷ houde mij voldaen door UE solutien daer op gegeven; die mij als in deese materie weynigh geoeffent niet te vooren en was [ge]komen. Ick geloove dat oock noch wel andere van UE problemata even soo veel difficulteyt hebben, die UE ongesolveert gelaeten heeft, als q⁶x⁶ ℞ qqry⁹ + ry¹¹. Alwaer mij nu niet anders voorkomt om te moghen stellen als qqry⁹ + ry¹¹ ℞ p³y⁹. Waer uyt komt yy ℞ p³ - qq^r / r, en xx ℞ py³ / qq. Voorts wat aengaet de utiliteyt van UE methode, die bestaet soo mij dunckt meest hierin om de gedaente van seeckere linien daer van UE de Equatie voorstelt uyt te beelden, en het waer te wenschen dat de methode om sulcx in alle Equatien te doen bekent waer. Het waer oock wel noodigh UE constructien hiertoe te doen dienen om de geheele gestalte der kromme linien voor ooghen te stellen. Als bij exempel in de Equatie aay ℞ x³, te doen sien dat de Paraboloides deese figuer⁴⁾ heeft en daerom A geen eygentlijck



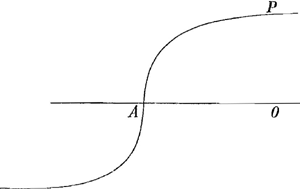
vertex en is. Het is voorts niet te twijffelen of UE manier in 't vinden der puncten is geometrisch, ende oock UE kromme linien alle van die soort die des Cartes voor Geometrische erkent. doch soo en kan men niet seggen dat het beschrijven van een kromme linie door gevonden puncten geometrisch ofte volkomen sij, of dat sulcke beschreven linien konnen dienen tot geometrische constructie van eenighe problemata, dewijl hiertoe, nae mijn opinie, geen kromme linien en konnen dienen als die door eenigh instrument vervolgens beschreven konnen worden, gelijck den Cirkel door een passer; en de Conische Sectien, Conchoides en andere door de instrumenten daertoe geinventeert. Want de linien met de handt van punt tot punt getrocken alleenlijck de gesochte quantiteyt ten naesten bij konnen geven en dienvolgens niet naer de Geometrische perfectie. Want wat helpt het sooveel puncten te vinden als men wil, indien men dat eene punct dat gesocht

4) C'est-à-dire: en prenant AO pour l'axe des y.

[p. 200]

werdt niet en vindt? Ende indien dese beschrijvingh door puncten tot de constructie der problemata goedt gekeurt wierdt, waerom en soude oock de deelingh van een circkelboogh in een gegeven reden, door de Quadratix van Dinostratus, niet voor geometrisch gehouden werden? dewijl men van deese oock sooveel puncten, en soo nae aen 't begeerde vinden kan als men begeert.

De constructien van het Problema van 't keerpunct in de Conchoides soo wel de uwe als de mijne⁵⁾ en moghen voor de rechte niet gehouden worden, dewijl het selve punct kan gevonden worden, sonder eenige conische sectie te gebruycken, als Heuraet over langh getoont heeft⁶⁾. Ick vinde onder mijne papieren eenighe diergelijcke constructien, die ick eertijds gesocht heb, nae dat de sijne was uijtgekomen,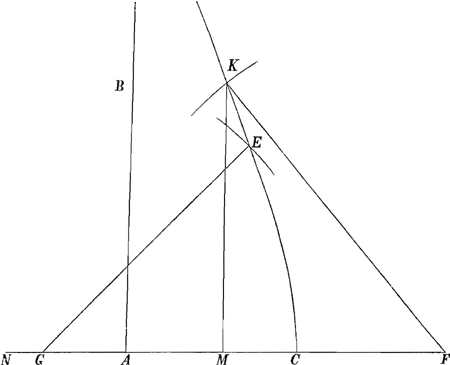



en onder anderen een die redelijk kort is⁷⁾, sijnde als volght. CE is de Conchoides. G het center. AC een diameter. AB de Asymptotos. Vindt een vijfde proportionael tot de linien 3 GA en 2 AC. welkers Proportionaels helft

5) Elle fut publiée dans les ‘Problematum quorundam illustrium solutiones’. Voir la Lettre N^o. 1068, note 3.

6) Voir la Lettre N^o. 641, note 6.

7) Dans le livre A des Adversaria p. 131. C'est à cette construction que se rapportent les mots: ‘Aliamque eadem ante multo faciliorem inveni, per circulum itidem et conchoidem ipsam quae data est’, de la Lettre N^o. 653.

[p. 201]

genomen van G tot F, soo beschrijft uyt het center F met den halven diameter FK diens quadraet gelijck is aen de quadraten AF en AC min het quadraet GA, de circumferentie HK⁸⁾ snijdende de Conchoides in K, waer van daen zij getrokken KM parall. met AB. en gelijck 3AG tot 2AC, soo sij AM tot AN. Voorts uyt het center G met den radius GE gelijk aen NC, beschrijft een circumfer. die de Conchoides doorsnijdt in E, soo is E het gesochte keerpunct.

8) C'est-à-dire: du cercle décrit de F comme centre avec le rayon FK. Dans la figure de la minute la lettre H, point d'intersection du cercle avec NF, a été biffée par mégarde (voir la note 1 de la pièce suivante).