Oeuvres complètes. Tome VIII. Correspondance 1676-1684

[p. 269]

N^o 2214.
G.W. Leibniz à Chris-tiaan Huygens.
Appendice au N^o. 2213.
26 janvier 1680.

La pièce se trouve à Leiden, coll. Huygens.
Elle a été publiée par P.J. Uylenbroek¹⁾ et par C.I. Gerhardt²⁾.

Exemplum²⁾ ex Nova mea Tangentium Methodo ductum^a).

Sit curva EE talis naturae, ut datis in recta AD velut axe quatuor punctis constantibus A.B.C.D et puncto curvae E, ac junctis quatuor rectis AE, BE, CE, DE tunc summa quatuor solidorum sub ternis quibuslibet rectis praedictis aequetur solido ex omnibus quatuor invicem ductis et datae rectae G applicatis facto; His positis ex puncto dato E tangens ET axi occurrens in T. ita educetur: Ex E demittatur in axem perpendicularis EF ponamus autem (facilitatis causa, ne signa mutare necesse sit) punctum F cadere inter A et T^*.

^*

1) Dans le deuxième fascicule de son ouvrage.

2) Dans la publication de Gerhardt, faite probablement d'après une minute de Leibniz, la suscription est conçue en ces termes: Specimen utilitatis Methodi novae Tangentium sive de maximis et minimis.

2) Dans la publication de Gerhardt, faite probablement d'après une minute de Leibniz, la suscription est conçue en ces termes: Specimen utilitatis Methodi novae Tangentium sive de maximis et minimis.

a) R. a d^o. Leibniz dum in Gallia agerem [Chr. Huygens].

* notandum tamen si punctum F cadat inter A et D mutanda nonnihil esse signa et pro summis adhibendas differentias certo modo sumtas.

* notandum tamen si punctum F cadat inter A et D mutanda nonnihil esse signa et pro summis adhibendas differentias certo modo sumtas.

[p. 270]

Hanc solutionem paucis calculi mei lineis invenio³⁾, per methodos autem publicatas quippe quibus irrationales tolli opus est, credo vix aliquot diebus inven-

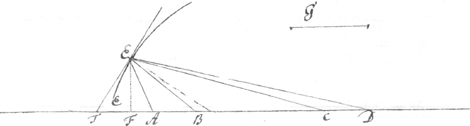
3) Posons EA = ϱ₁, EB = ϱ₂, EC = ϱ₃, ED = ϱ₄, on aura selon la définition de Leibniz:
ϱ₁ϱ₂ϱ₃ + ϱ₁ϱ₂ϱ₄ + ϱ₁ϱ₃ϱ₄ + ϱ₂ϱ₃ϱ₄ = ϱ₁ϱ₂ϱ₃ϱ₄/g........(1).
De nos jours, on écrirait:
1/ϱ₁ + 1/ϱ₂ + 1/ϱ₃ + 1/ϱ₄ = [1/ϱ] = 1/g............(2),
et on définirait la courbe comme celle pour laquelle est constante la somme des courbures de quatre cercles, passant par un point de la courbe et ayant leurs centres donnés sur une même droite.
Si l'on choisit cette droite comme axe des abscisses et que l'on désigne les abscisses des centres donnés par a₁, a₂, a₃ et a₄, l'équation (2) peut s'écrire
[((a - x)² + y²)^-½] = g^-1.
Au moyen de l'algorithme du calcul différentiel que Leibniz, dans la Lettre N^o. 2205, dit avoir trouvé (voir la note 4 de cette Lettre), on obtient immédiatement:
TF:EF = dx:dy = [yϱ^-3]:[(a - x)ϱ^-3]
ou bien, selon l'énoncé du théorème de Leibniz:
TF:EF = [y(g/ϱ)³]:[(a - x)(g/ϱ)³].
On voit qu'on pourrait augmenter le nombre des points A, B, C, D, sans compliquer le calcul d'après l'invention de Leibniz. S'il s'est borné à quatre, c'est probablement pour pouvoir identifier avec des solides chacun des termes de son équation primitive (1). Dans l'article cité dans la note 4 de la Lettre N^o. 2205, Leibniz a proposé un exemple pareil: mener la tangente à une courbe pour laquelle est constante la somme des distances d'un point à six autres points donnés sur une même droite.
L'exemple proposé dans notre Lettre était assurément bien choisi pour montrer la supériosité de la nouvelle méthode de Leibniz, savoir la différentiation directe des fractions et des irrationelles, comparée aux méthodes algébriques antérieures. Toutefois, la lettre de Huygens à Leibniz du 9 octobre 1690 témoigne que ce spécimen n'avait pas suffi pour convaincre Huygens.
Lorsque Huygens, en 1680, reçut de Leibniz la Lettre N^o. 2213 avec le problème, la pièce N^o. 2214, il était souffrant. En 1680 de fréquentes indispositions annonçaient déjà sa grave maladie de 1681. Après son retour en Hollande, le manuscrit paraît de nouveau être tombé dans ses mains; il y annota en latin ‘reçu de M. Leibniz, lorsque je vivais en France’. Autant qu'on peut en juger par les ‘Adversaria’, Huygens ne s'est occupé du problème de Leibniz que vers mars 1687. En cherchant la solution de problèmes du même genre, il ne manqua pas de trouver par des considérations géométriques une méthode directe et simple, propre à les résoudre et qui, appliquée au problème de Leibniz, en donnait la même solution.
Dans les ‘OEuvres inédites’ qui suivront cette Correspondance, nous aurons l'occasion de revenir sur ces recherches de 1687. Uylenbroek les a reproduites en partie dans le Fasciculus II, pp. 23-28, de sa publication (Lettre N^o. 2057, note 2).

[p. 271]

tum iri, et fortasse ne vix quidem. Tollendo enim irrationales assurgetur ad altissimos gradus quod non sine taedio fieri potest; et tamen postea, cum valores aut constructiones quaerimus, cogemur aequationis, inutiliter exaltatae, iterum depressiones investigare, qui labor in aequationibus decimum longè gradum excedentibus (qualis ista foret) saepe immensus est.