Oeuvres complètes. Tome VII. Correspondance 1670-1675
(1897)–Christiaan Huygens–
[pagina 197]
| |
No 1897.
| |
[pagina 198]
| |
Sed fortasse tibi non erit ingratum intelligere, quâ viâ ad hanc constructionem pervenerim: scias itaque, me ex priore mea Analysi deduxisse hoc modo. Datis ijsdem quae prius, cadat in EB normalis AO, sitque punctum quaesitum P, ex quo in AO cadat normalis PR. Si AO sit b; EO, z; OB, d; AP, q; PR, e; AR, a; facile colligitur haec aequatio
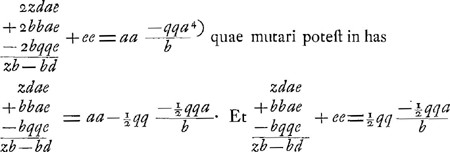 Ga naar voetnoot4) Hujus ultimae constructionem olim ad te misiGa naar voetnoot5), alterius vero Clarissimus Hugenius. Primum autem, licet se statim in conspectum dedisset, fermè neglexeram, difficilioris constructionis esse praesumerem. Sed me vano timore delusum agnovi, cùm in hanc, quam ad Te mitto, constructionem desinere nuper sum expertus. Sit enim, brevioris calculi causâ, 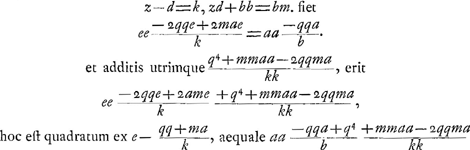 Fiet igitur ἀναλογισμῶς 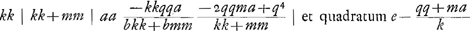 qui ad aequationem faciliorem reduci potest, si posito kk + mm = pp fiat ky/p = a; fit enim tandem, quadratum ex 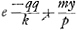 aequale aequale 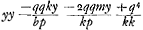 ; quam aequationem constructioni superiori respondere ; quam aequationem constructioni superiori respondere
| |
[pagina 199]
| |
animadvertes, si calculos applicueris; ac simul observabis, ad quamcumque linearum EA, AB, BE referatur analyseos summa, easdem semper haberi posse sectiones, quamvis longiore circuitu et aequationibus valde diversis. Ex hoc constructione ϰατ᾽ ἀναλογίαν deducere licet alterius Problematis effectionem, cùm scilicet quaeritur punctum à quo radius reflexus parallelus sit cuilibet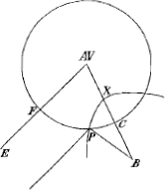 lineae datae. Ut si dato puncto luminoso B, circulo ex centro A, quaereretur radius reflexus parallelus rectae AE. Idem enim est, acsi, in alio Problemate, distantia punctorum A et E supponeretur infinita; quo casu tertia proportionalis ipsarum EA, FA, abiret in nihilum, et puncta A et V coinciderent. Itaque VX esset aequalis AX, et AE parallela PE. Applica igitur superiorum constructionem et Problema absolves; descriptâ scilicet (vertice X, latere transverso VX, vel AX, et recto ipsi aequali), hyperbolâ XP, cuius applicatae ad diametrum AX, parallelae sint rectae AE. |
|