Oeuvres complètes. Tome VII. Correspondance 1670-1675

[p. 147]

N^o 1869.
R.F. de Sluse à H. Oldenburg.
6 janvier 1672.
Appendice au No. 1868.

La copie se trouve à Leiden, coll. Huygens¹⁾.
La lettre a été publiée par M. le Paige²⁾.

Copia Epistolae Clarissimi Slusii ad H.O. die 6. Cal. Jan. 1672 circa Problema Alhazeni; etc.

Caeterum à Clarissimo Hugenio nihil adhuc accepi³⁾, aliis, ut existimo, studiis occupato. Quoniam autem Tu, Vir Clarissime, videri vis, meas esse aliquid putare nugas, accipe, quae circa Alhazeni problema, curis secundis, meditatus sum.

Datus sit circulus, cujus centrum A; puncta data sint D et d. Supponatur factum quod quaeritur, sitque radius incidens DE, reflexus Ed; et ex puncto reflexionis E cadat in junctam DA normalis EI, et in eandem, ex d, normalis dN, occurrantque eidem tangens EC, et radius dE productus in B.

Sit nunc DA//z. AI//a. NA//n. EI//e. dN//b. BA//y. AE//q. CA//x. Igitur cum anguli DEC, CEB, sint aequales, et angulus CEA rectus, ex hypothesi, erunt tres DA, CA, BA, harmonicè proportionales (hoc enim facile ostenditur). Erit itaque ut DA ad BA, ita DC ad CB. Sive in terminis analyticis, z/y/z-x/x-y. et 2zy-xy//zx sive 2zy/z + y//x.

Cùm autem rectangulum CAI, sive

1) La copie est de la main d'Oldenburg.

2) Le N^o. 106 de la Correspondance de René-François de Sluse. La copie envoyée par Oldendenburg à Huygens la reproduit presque en entier. La lettre fait partie du résumé, mentionné dans la Lettre N^o. 1837, note 14.

3) Consultez la Lettre N^o. 1853, note 7.

[p. 148]

xa sit aequale quadrato AE sive qq, erit x//qq/a, et per consequens 2zy/z + y//qq/a sive zqq/2za-qq//y. Porró est ut dN ad EI, ita NB ad IB, sive b/e/y-n/y-a.

Itaque ye-ne//by-ba; et y//ba-ne/b-e. Igitur zqq/2za-qq//ba-ne/b-e sive 2zbaa - 2znae - qqba + qqne//bzqq - zqqe. Quae aequatio est ad hyperbolam circa asymptotos, cujus constructio cum circulo dato, problemati satisfacit. Cum vero, ob circulum, sit qq//aa + ee, si loco 2bzaa ponatur ejus valor 2bzqq - 2bzee, habebitur alia pariter ad hyperbolam circa asymptotos, bzqq - 2bzee - 2znae - qqba + qqne//- zqqe: et hac methodo, atque illâ, quam in libello nostro de Analysi exposuimus, prodibunt infinitae aequationes ad hyperbolas et ellipses, quae cum circulo dato problema absolvent; nisi quod effectiones plaerunque intricatiores evadant, quam ut operae precium sit illas aggredi. Construi tamen poterunt eo modo, quo usi sumus in Ellipsi, ejusdem libelli nostri p. 62.

Retulimus, ut vides, calculi nostri summam ad lineam DA, sed satis animadvertis, non majori difficultate referri potuisse ad dA (quae pariter data est) ductis scilicet lineis, quas in schemate punctis adumbravimus. Verum novo calculi labore non est opus. Si enim rectae dA ejusque partibus eosdem, ac prius, terminos analyticos adhibeas, hoc est, si ipsam dA facias aequalem z, Dn//b, nA//n. Ai//a. iE//e &c. prodibit eadem aequatio quae prius; et infinitas alias hyperbolas et ellipses obtinebis, quae cum circulo dato Problemati satisfacient.

Φορτιϰὸς essem, si singulos casus prosequi vellem, cúm illorum aequationes solâ signorum + et - variatione discernantur. Unum tamen excipio, nimirum cum angulus dAD est rectus; ejus enim aequatio habetur, ex punctis à priori aequatione partibus, in quibus n (quae in nihilum abit) invenitur: nempe haec 2zbaa - qqba//bzqq - zqqe, vel (pro 2zbaa posito ejus valore) zbqq - qqba//2zbee - zqqe. Sed animadvertendum est, quod, licet referendo analysin ad rectam DA, statim sese offerant in aequatione duae Hyperbolae; et aliae totidem à prioribus diversae, cúm refertur ad rectam dA; easdem tamen omninó parabolas haberi, ad utramvis rectarum dA vel DA referatur analysis: cujus rei ratio levi consideratione tibi occurret.

Patere nunc V.C. ut superiorem analysin omnibus, quae circa speculorum sphaericorum reflexionem proponi solent, Problematibus applicem, novo facto schemate.

Sit igitur, ut prius, circulus cujus centrum A, punctum D datum, et ab eo radius incidens DE, cujus reflexus sit EQ; junctâ DA, ducatur ad illam tangens EC, et normalis EI; et producatur ad eandem, recta QEB. Denominentur partes ut prius, DA//z. CA//x. AE//q. BA//y. AI//a. IE//e. Igitur propter tres DA, CA, BA, harmonicè proportionales, et tres CA, AE, AI, Geometricè, semper habebitur aequatio y//zqq/2za - qq, in quodcumque circuli punctum cadat radius

[p. 149]

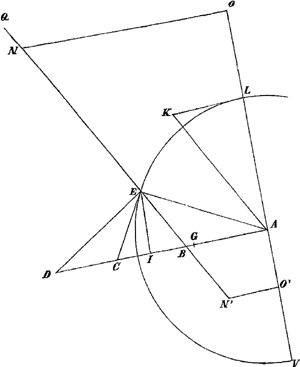DE. Itaque si quaeratur punctum E, in quod si radius DE incidat, reflectatur παραλλήλως diametro LAV normali ad DA; reflexus QE productus transibit per I, ut patet, et I ac B coincident. Igitur a//y//zqq/2za - qq, sive aa - ½qqa/z//½qq, et problema per plana solvetur.

Si quaeratur punctum, à quo radius reflectatur parallelus alteri cuilibet lineae, ut AK (ducta ex centro A;) ducatur ad illam ex puncto I⁴⁾, tangens KL//d; evidens est, triangula ALK, EIB, fore similia, cum omnia latera unius parallela sint lateribus alterius &c. Itaque AL ad LK ut EI ad IB, sive q/d/e/a - y. et qa - de/q //y// zqq/2za - qq. et zq³//2qzaa - 2zdae - q³a - qqde⁵⁾. Sive, pro aa posito qq-ee, zq³//2zq³ - 2zqee - 2zdae - q³a + qqde. Utraque autem aequatio est ad hyperbolam circa Asymptotos, quae cum circulo dato Problema absolvit.

Proponatur nunc efficere, ut radius reflexus transeat per datum punctum N (ut in problemate Alhazeni) vel ut productus versùs punctum reflexionis E occurrat dato puncto N. Ex N cadat in AL normalis NO//n, sitque AO//b. Patet esse ut AO ad differentiam ipsarum ON, AB, ita EI ad IB, hoc est, b/n - y/e/a - y, vel b/y - n/e/a - y. Igitur ba-ne/b-e//y//zqq/2za-qq. Unde 2zbaa - 2znae - qqba + qqne //bzqq - zqqe, nimirum illa aequatio Problematis Alhaseniani, quam supra invenimus. Vel 2^do casu ba + ne / b + e//y//zqq/2za - qq sive 2zbaa + 2znae - qqba - qqne//zbqq + zqqe: de quibus aequationibus plura non addo, cum vel nimia sint fortasse quae supra diximus.

4) Lisez: L.

5) Lisez: + qqae.

[p. 150]

Atque haec sunt problemata, quae circa punctum reflexionis proponi solent, in quibus tamen finitam puncti D dati distantiam supposuimus. Sed facilior erit Analysis, si supponamus infinitam. Sectâ enim CA bifariam in G, constat ex proprietate trium DA, CA, BA, harmonicè proportionalium, tres DG, CB⁶⁾, BG, fore geometricè proportionales, suppositâ quacunque puncti D distantiâ. Itaque si supponatur infinita, BG abibit in nihilum, et punctum B cum puncto G coincidet. Igitur AB erit perpetuò aequalis BC. Erit itaque CA//2y, et rectangulum CAI, aequale quadrato AE, dabit in terminis analyticis, 2ay//qq, sive y//qq/2a; cumque distantia puncti D supponatur infinita, erit ED parallela AC. Itaque si quaeratur radius reflexus parallelus AL, quoniam eo casu a et y coincidunt, erit a//y//qq/2a sive aa//½qq.

Si quaeratur ut parallelus sit AK, erit rursus q/d/e/a - y, et qa - de/q//y//qq/2a. Sive 2qaa - 2dae//q³.

Si petatur, ut transeat per N, erit ut supra ba ± ne / b ± e//y//qq/2a et 2baa ± 2nae//bqq ± qqe.

Quae aequationes sunt quoque ad hyperbolas circa asymptotos, nisi N punctum esse supponatur in AL: nam cum tunc n abeat in nihilum, sublatis ab aequatione partibus in quibus n continetur, residuae dant aequationem ad parabolam, ut supra quoque monuimus.

Non exspectas, ut cúm specula concava⁷⁾ hactenus in exemplum adduxerim, nunc agam de convexis⁸⁾. Scis enim, eandem esse prorsus analysin, et aequationes solâ signorum + et - variatione distingui. Scis, parabolam vel ellipsin, quae uni satisfacit, satisfacere alteri; et si hyperbola in convexo Problema absolvat, ejus oppositam paria facere in concavo.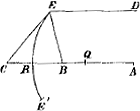

His itaque omissis, addo tantum, eâdem analysi haberi in speculis concavis focos et spatia, quae radii occupant in axe, datâ qualibet puncti lucentis distantiâ: sed mira facilitate cúm radii supponuntur paralleli; quod tamen nonnullo circuitu a quibusdam demonstrari vidi. Nam in speculo concavo EE, cujus centrum A, si radius extremus reflecti intelligatur ad axem AR in B, ductâ tangente E⁹⁾, erit CB aequalis BA. Bisecetur semi-axis AR in Q; erit itaque Q focus et QB spatium quaesitum. Est autem QB dimidia CR (ob aequales AQ, QR, AB, BC), hoc est, dimidia excessûs secantis arcûs ER supra sinum totum.

6) Lisez: CG.

7) Lisez: convexa.

8) Lisez: concavis.

9) Lisez: EC.

[p. 151]

Igitur si arcus ER sit exempli gratia grad. 9, erit AC 101246, et BQ 623/1000000¹⁰⁾ ipsius AR.

Sed nimium te moror &c.

10) Lisez: 63/100000.