Oeuvres complètes. Tome I. Correspondance 1638-1656

[p. 505]

N^o 342.
Christiaan Huygens à P. de Carcavy.
12 octobre 1656.

La minute et la copie se trouvent à Leiden, coll. Huygens.
La lettre est la réponse au No. 336.

12 Oct. 1656.

Carcavy.

Monsieur

Je vous suis fort obligè de la peine qu'il vous a pleu prendre en envoyant a Monsieur Fermat l'exemplaire de mon petit livre et la solution que j'avois donnée aux problemes qu'il avoit proposè. J'espere qu'il l'aura approuvée comme aussi Monsieur Pascal puisque vous ne me faites pas entendre le contraire.

Dans le Theoreme dont vous dites que ce dernier se sert de mesme que moy il y a quelque faute, qui ne vient pourtant pas de luy, mais que j'impute a la haste que vous avez eue a le descrire. Car asseurement Monsieur, vous avez voulu dire, Qu'ayant multipliè chasque nombre de hazards, par le nombre des pistoles, que ces hazards donnent, il faut adjouster tous les produits ensemble et les hazards ensemble et diviser l'un par l'autre; et qu'ainsi le quotient sera le requis. Et il est vray que c'est la mesme enonciation que la miene.

Or de cette reigle je m'en sers aussi dans l'exemple que vous avez proposè, à scavoir quand on joue en 6 parties ou d'avantage, et que l'un des deux joueurs a une partie ou deux ou 3 &c. a point. Et quoyque ce ne soit pas avec la mesme brievetè qu'apporte celle de Monsieur Pascal au cas que l'on a une ou deux parties à point; Elle est toutefois fort universelle, et je croy que dans les autres cas aux quels celle de Monsieur Pascal ne s'estend point, il se sert de la mesme ou d'une semblable, et que mesme sans l'ayde d'une telle il n'est pas parvenu a la siene qui est a la verite fort compendieuse et belle.

la proposition qu'il a faite à Monsieur de Fermat me parut d'abord assez embarassante, mais j'ay veu bientost qu'il n'estoit question que de cecy, a scavoir, que l'un des joueurs marquant un point lors qu'il arrive 11 de trois dèz, et l'autre marquant un point lors qu'il arrive 14, et celuy de deux gaignant qui le premier aura marquè 12 points d'avantage que l'autre, il faut determiner l'avantage de chacun d'eux. Le Probleme estant fort joly à mon advis, et voyant que Monsieur Pascal l'avoit jugè si difficile qu'il doubta si Monsieur de Fermat en pourroit venir à bout je n'ay peu m'empescher d'en chercher aussi la solution, quoyque vous m'ayez envoyè celles que tous les 2 en ont faite. Je me suis tousjours servij du mesme theoreme que dessus, et par le moyen de cettuylà et de l'algebre j'ay trouvè la reigle generale pour cette question, qui est fort simple comme vous verrez. Estant donnè telles chances que l'on voudra de 2 ou trois ou plusieurs dez, et

[p. 506]

quelque nombre que ce soit des points qui finissent le jeu, il faut voir premierement combien de hazards il y a pour chascune des chances ou deux autres nombres dans la mesme raison. les nombres de ces hazards estants multipliez chacun en soy mesme autant de fois qu'il y a de poincts qui finissent le jeu, les produicts auront entre eux la proportion requise des avantages. Par exemple dans le cas que Monsieur Pascal a proposè, il y a 27 hazards pour la chance de 11, et 15 hazards qui donnent 14. Or comme 27 à 15 ainsi est 9 à 5. il faut donc multiplier le 9 et le 5 chacun douze fois en soy mesme, parce que l'on joue en 12 points; les produicts sont 282429536481 et 244140625, que je dis exprimer la vraye proportion des avantages. aussi ont ils entre eux la mesme raison que ceux de Monsieur Pascal qui estoyent 150094635296999121 et 129746337890625, et ils sont les plus petits qu'il soit possible de trouver. Si la chance de l'un soit 10, et celle de l'autre 13, et qu'ils jouent en 10 points, les avantages seront par cette regle comme 3486784401 a 282475249, et si les chances soyent 13 et 17, en jouant en 12 points, l'avantage de l'un a celuy de l'autre sera precisement comme 13841287201 à 1. ce qui semblera d'abord assez estrange^a).

La methode dont j'ay trouve la regle m'enseigne aussi en mesme temps d'en faire la demonstration qui seroit pourtant bien longue.

Faites moy la grace je vous prie de communiquer tout cecy à Monsieur Milon, et aussi à Monsieur de Roberval, puis que vous le voyez quelquefois. afin que je n'aye pas besoin d'escrire plusieurs fois une mesme chose.

Je ne veus pas vous donner la peine de lire une lettre¹⁾ par la quelle j'ay respondu au Jesuite Ainscom et que j'ay fait imprimer. Il me suffit que vous scachiez que je suis pas demeurè sans replique dans une si bonne cause.

Ce qu'il y a de plus remarquable dans l'Arithmetica Infinitorum de Monsieur Wallis que vous dites n'avoir encore veue c'est cette progression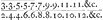 qui est une fraction: dont le dessus est le produit de tous les nombres 3.3.5.5 &c. multipliez ensemble: et le desous le produit des nombres 2.4.4.6.6 &. Il a trouuè que cette fraction estant continuee à l'infiny le denominateur est au numerateur comme le cercle au quarrè de son diametre, qui est une speculation assez belle, quoy que de peu d' usage, si ce n'est qu'il en tire d'autres consequences cy apres. Car bien qu'il adjouste a cecy une maniere plus courte pour approcher aussi pres que l'on veut de la vraye proportion, la maniere ordinaire pourtant par les polygones inscrits et circonscrits l'est encore beaucoup plus. Au reste la demonstration qu'il en donne n'est pas bien evidente et je douterois encore si la chose estoit vraye s'il me m'asseuroit que l'on en a essayè la veritè jusques à la 10^e lettre, et trouuè que la proportion de la circonference au diame-

a) Demonstration à Mylon [Chr. Huygens].

1) C'est l'imprimé de la Lettre N^o. 338.

[p. 507]

tre est entre 3.1415926535, 69 et 3.1415926536,96 à 1²⁾. Ce qui me fait croire qu'il ne s'est pas trompè. Je suis

Monsieur

Vostre treshumble et obeissant serviteur Chr. Huygens de Zulichem.

2) Voir la Lettre N^o. 325.