Oeuvres complètes. Tome I. Correspondance 1638-1656

N^o 325.
J. Wallis à Christiaan Huygens.
22 août 1656.

La lettre se trouve à Leiden, coll. Huygens.
Elle est la réponse au No. 316. Chr. Huygens y répondit par le No. 337

Celeberrimo Clarissimoque Viro Domino Christiano Hugenio Joh. Wallis. S.

Literas tuas (Vir Clarissime) Julij 21 datas ego ante quatuor dies accepi, quibus ob Clarissimi Viri Domini Erasmij Bartholini jam proxime abituri¹⁾ decessum necesse habeo raptim respondere. Quod tibi non displicuerit qualiscunque opera mea, quinimo accepta fuerit, etiam gaudeo. Ubi aliquid haerere tibi visum est, id facili, spero, negotio amovebitur, quippe illud non profundae difficultatis videtur, sed quod ipse amovisse possis, iteratâ inspectione, aut etiam de facto amoveris forsan priusquam hae ad te perveniant. Progressionem illam quod attinet cur non in dubium vocem id facit, quòd continuâ methodo eò pervenerim, ut ubi totum processum examinaveris reperies: nec uspiam videam ubi de errore admodum dubitandum videatur. Quod autem examen per numeros fieri suadeas, quamquam ea de re minus ipse fuerim solicitus, id tamen jam sua sponte praestitit Honoratissimus Dominus, Vicecomes Bronker²⁾, (cujus ad propositionem 191 mentio-

1) En septembre il était sur son retour en Hollande, voir la Lettre N^o. 335.

2) Lord Viscount William Brouncker naquit à Castle Lyons (Irlande) vers 1620 et mourut à Londres le 5 avril 1684. Il était zélé royaliste, aida à la restauration de la royauté et devint alors Lord Chancellor, Lord of the Privy Seal et Commissionary to the Navy; il était encore Master of St. Catharine Hospital à Londres, et en outre un des premiers membres, et pendant quelque temps président, de la Société Royale.

[p. 477]

nem facio) quò tam suam quam meam designationem comprobet; atque examen illud ad decimum usque locum continuavit, omniaque ex voto succedentia invenit; scilicet rationem Perimetri ad Diametrum inde colligit

{ majorem quam 3.14159,26535,69 + } ad 1.

{ minorem quam 3.14159,26536,96 + } ad 1.

Sed et in toto processu, alternatim, nunc excedentem nunc deficientem, ut oportuit; utrinque autem ad justam continuè propius accedentem: ut non dubium sit quin eò ritè pervenerim investigando.

Quod autem ad Demonstrationis modum per Inductionem attinet, quem novo exemplo in Geometriam me putas introducere. Quamquam non negem me aliquid hic novi praestitisse; cum ea methodo frequentius videar atque apertius usus; non tamen id plane novum est, aut omni exemplo caret quo me hoc nomine defendam, nam et id frequentius fit quam tu forte primo aspectu putaveris: praesertim in Arithmeticis. Nempe ubi seriatim non videant aliquousque procedere, nec quicquam in contrarium urgeri posse praevideant, universaliter rem asserunt etiam accurati Mathematici. Videbis id aliquoties (ni fallet memoria) a Domino Briggio³⁾, Praecessore olim meo meritissimo, inter Regulas eas quas praeposuit Tabulis suis Logarithmicis⁴⁾, ubi de Constructione Canonis leges exhibet; nec tamen eapropter Canonis Logarithmici fides suspecta fuit. Similiter in ijs quae a Vieta praestita sunt de Angularibus Sectionibus⁵⁾; ubi postquam series aliquousque comprobata est, quod superest in Tabellas conjicitur in infinitum continuendas. Sed et ipsae Tabellae numerorum qui in artificiosa Potestatum Genesi usui sunt, non nisi ex incepta serie, aliquousque comprobatâ calculo, deinde continuantur in infinitum; quae non aliter quam Inductione probantur. Verum et in alijs propositionibus Geometricis id passim usu venit: ut, verbi gratia, in 34 propositione 5 Elementorum ex editione Clavij⁶⁾, (alijsque passim). Nempe propositio incipit. Si sint

3) Henry Briggs, né en février 1561 à Warley-Wood (Yorkshire), mourut le 26 janvier 1630 à Oxford. Il fut professeur de mathématiques à Gresham College (1596), puis à Oxford (1619). Il est renommé pour sa part dans le calcul des logarithmes et laissa en outre plusieurs ouvrages.

4) Arithmetica Logarithmica sive Logarithmorvm Chiliades triginta, pro numeris naturali serie crescentibus ab vnitate ad 20.000: et 2 90.000 ad 100.000. Quorum ope multa perficiuntur Arithmetica problemata et Geometrica. Hos nvmeros primvs invenit Clarissimvs Vir Johannes Nepervs Baro Merchistonij: eos autem ex ejusdem sententia mutavit eorumque ortum et vsum illustravit Henricvs Briggivs, in celeberrima Academia Oxoniensi Geometriae professor Savilianvs. Devs nobis vsvram vitae dedit et ingenii, tanqvam pecvniae, nvlla praestitvta die. Londini. Excudebat Gvlielmvs Iones. 1624. in-folio.

5) Voyez Francisci Vietae Opera Mathematica, la partie i: Sect: ix, Theoremata ad Sectiones Angulares, p. 287-304.

6) Evclidis Elementorvm Lib. xv. accessit xvi. de Solidorvm Regularium cuiuslibet intra quodlibet comparatione: Omnes perspicvis demonstrationibus, accuratisq; scholijs illustrati, nunc iterum editi, ac multarum rerum accessione locupletati. Avctore Christophoro Clavio Bambergensi è Societate Jesv. Romae apvd Bartholomaevm Grassium. mdlxxxix. Permissv Svperiorvm. ii vol. in-8^o.

[p. 478]

quotcunque magnitudines &c. Deinde probat inductione, Sunto, inquit, tres & c. Deinde sint quatuor &c. Et tum subjungit, Eadem arte concludes ea consequi in quinque, sex, septem &c. Non secus atque nos, puta propositione 19. Sint termini duo; proveniet ratio ⅓ + ⅙, quod demonstratur ex calculo. Sicut tres, proveniet ratio 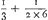quod item demonstratur ex calculo. Et sic deinceps quousque libet, nempe ubique demonstratur ex calculo. Imo, inquam, (quod tamen non omnes animadvertunt) vix ulla est in tota Geometria propositio quae aliter quam inductione demonstratur. Exemplum esto 121. Propositio Euclides, Super data quavis recta terminata, triangulum aequilaterum constituere. Deinde exponit unam rectam AB, et super hanc constructum triangulum demonstrat esse aequilaterum: Tum subsumendum relinquit, (quod nempe quilibet supplere debet,) Atque eadem methodo, super quamvis aliam rectam ita construetur triangulum, et pariter demonstrabitur. Ergo, In quavis &c. Nec quidem aliter constat vis istius aliusve fere demonstrationis, quam ex suppositione, quod nullus casus in contrarium urgeri possit cui non applicabitur exposita demonstratio: quam qui suppositionem negaverit, tenetur casum contrarium assignare. Similiter, ubi nos non unum quidem aut duo exempla, sed 6, 7, 8 &c. (vel etiam, quod in adversarijs nostris aliquando fecimus, ad locum etiam centesimum, aut ultra;) idem universaliter obtinere contendimus, nec quisquam exemplum in contrarium urgere poterit: Non est cur ea pro legitima demonstratione non habeatur. Sed et pares inductiones videbis ad 20e 6, et 1e 12⁷⁾, et passim alibi. Et apud Archimedem fere ubique. Nempe in Theoremate sive Problemate ubi casuum numerus certus est atque finitus; solent Mathematici singulos casus sigillatim probare. At ubi numerus casuum est infinitus, satis habent, si, ostensis paucis, methodum item ostendant qua qui volet quotlibet demonstret alias. Nec quidem alias demonstrationes ejusmodi propositiones patiuntur; utut illud nonnunquam planius, nonnunquam magis tectè instituatur.

Dum autem ais ad propositionem 191. te non bene intelligere quo pacto ex eo quod β/a minor sit quam 2/1, conficiam eandem β/a minorem esse quam √ 2/1; et similiter γ/b minorem esse quam 4/3, adeoque et quam √ 4/3. Neutiquam assequeris, ob festinationem, quod illic traditur, quod tamen iteratâ inspectione non dubito quin statim videris. Nempe quia β/a = 2/1, concludo β/a (non gb/a) minorem quam √ 2/1. Velim itaque ut haec verba mea, Ideoque (cum rationes continuè multiplicantes perpetuo decrescant) erit

7) Wallis désigne ici probablement la proposition 20 du livre 6, et la proposition 1 du livre 12 des Eléments d'Euclide.

[p. 479]

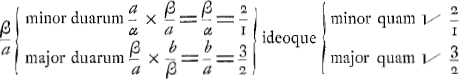quasi sic dicta intelligas. Quoniam seriei α. a. β. b. γ. c. &c. rationes β/a. b/a. γ/β. c/b.&c. perpetuo decrescunt, (ut superius patet,) adeoque et, interpolatione regulari continue factâ, rationes quae componunt has expositas, nempe a/α, β/a, b/β, γ/b c/γ, δ/c&c. continue item decrescunt: Erit ideo β/a minor duarum a/α, β/a, componentium rationem β/α = 2/1; adeoque eadem β/a (cum sit minor duarum componentium rationum β/α) erit minor quam √ β/α = √ 2/1 (nam duarum rationum aequalium, componentium aliam, utraque erit ratio subduplicata compositae: et inaequalium eandem compositam componentium, minor quidem, minor erit quam ratio subduplicata; et major, major).

Item eadem β/a (cum sit major duarum β/a, b/β, componentium rationem b/a = 3/2) erit major quam √ b/a = √ 3/2. Similiter est item

Denique quod ad ultimum tuum quaesitum attinet. Num scilicet curva propositionis 192. sit Geometrica, necne. Nescio num de hac sola, an de alijs illam propositionum sequentium, et scholij, curvis procedat. Si enim reliquas pro Geometricis admiseris, de hac, eadem ratione constabit, ut mox videbitur. Sin eas non admiseris; dicendum erit quatenus ego id contendam. Nempe de Scholij ultimi curvis 2a, 4a, 6a, 8a &c. res statim erit in confesso; quarum nempe singula puncta determinantur per aequationes monadicam⁸⁾ lateralem⁹⁾, quadraticam, cubicam, &c. quae quidem ad propositionem 189. exhibentur. De reliquis 1^a, 3^a, 5^a, 7^a &c. videntur illae postulare

8) C'est ainsi que l'auteur appelle une équation exprimant l'invariabilité d'une fonction.

9) Wallis emploie ici la locution vieillie ‘aequatio lateralis’ pour ‘équation du premier degré’.

[p. 480]

aequationes, quae sint istis intermediae; puta 3^a postulat aequationem naturae intermediae inter monadicam et lateralem; 5^a, aequationem quae sit inter lateralem et quadraticam intermedia; 7^a, ea quae est inter quadraticam et cubicam intermedia. Has autem ego aequationes, utut determinatae in rerum natura quantitatis existimem, puto tamen ineffabiles¹⁰⁾ esse; quamquam interim earum unâ cognitâ, reliquas etiam cognosci certum sit, ex demonstratis propositionibus 188, 189. Si verò quod ineffabiles sint illae aequationes, vel saltem adhuc esse videantur, propterea nec lineas eas pro Geometricis agnoscas, utut sint in rerum natura satis determinatae, licèt nobis haud effabili aliqua aequatione determinandae; ego litem de nomine non movebo. Videntur autem hujusmodi aequationes ita se ad effabiles habere, atque numeri surdi ad veros. Si autem et eas lineas pro Geometricis habendas putes, (nam pro Geometrarum arbitrio vel sunt vel non sunt ita dicendae,) erit et pariter Geometrica ea quae est Propositionis 192. Est enim haec ab earum aliquâ facile derivabilis, quippe 1. 3/2. 15/8. 105/48 &c. numeri curvae propositionis 193. (quae eadem est cum scholij curva tertia) ducti in Geometrice proportionales 1. 4. 16. 64 &c, constituunt numeros curvae propositionis 192. adeoque et numerorum illis interpolandorum mutuo ductu, fiunt qui hic interpolandi; adeoque si curva propositionis 193. sit linea Geometrica, erit item et linea propositionis 192. Habenda itaque est pro Geometricâ, vel utraque vel neutra. Si autem lineae genus, in natura rerum utcunque determinabile ego verbis in propositione 192. non satis determinaverim; id verborum penuriae in re difficili dandum est.

De Saturno nil novi dicendum habeo. Quando ipsius restituentur ansulae, res exspectamus magis quam praedicimus. Saturni phases hic visas, spero, aeri incisas me tibi brevi communicaturum. Jd nempe se curaturum mihi est pollicitus Dominus Christophorus Wren. Jnterim Vale.

Raptim Oxoniae

Augusti 12. 1656.

Celeberrimo Clarissimoque Viro, Domino Christiano Hugenio Constantini filio,

tradantur

Hagae Comitis.

10) L'auteur désigne par ces mots des équations de degré ½, 3/2, 5/2, qu'on pourrait nommer des équations ‘sourdes’ ou irrationnelles.