Oeuvres complètes. Tome I. Correspondance 1638-1656

N^o 316.
Christiaan Huygens à J. Wallis.
[21 juillet 1656]¹⁾.

La minute et la copie se trouvent à Leiden, coll. Huygens.
J. Wallis y répondit par le No. 325.

Sommaire:
Librum accepi. Schotenio misi qui emerat. gratias pro libro, pro honorifica nostri mentione. de Ainscomio. de progressione. operae praetium ut examinet per numeros. demonstratio claudicat propos. 53. 187. ut non sit dubium quin idem de vacuis credendum sit. prop. 191. β/α minor quam 2/1 ideoque minor quam √2/1 lineam curvam pr. 192 non esse determinatam. in curvis geometricis quotlibet puncta inter duo data inveniri possunt.

Clarissimo Viro Domino Joh. Wallis. Chr. Hugenius S.D.

Libros quos ad me miseras posteaquam diu hic in officina bibliopolae delituissent tandem paucis abhinc diebus accepi, cumque Domino Schotenio exemplar alte-

1) Cette date résulte de la réponse, la Lettre N^o. 325.

[p. 459]

rum deferri curassem, rescripsit ille se jam ante sibi comparasse. Quod sanè et ipse fecissem, si scivissem Lugduni illos venire. Plurimum tibi debeo, quod mentionem nostri facere voluisti nec sine laude²⁾, quando operosam Gregorij a Sto Vincentio quadraturam εξετασει mea labefactam judices. Nihil mihi exoptatius evenire potuit praesertim hoc tempore, cum novis conatibus easdem illas ineptias propugnari cernam. Ainscomius enim Jesuita Patris Gregorij discipulus librum à se editum mihi nuper misit, quo quotquot sunt novae quadraturae adversarij refelluntur, scilicet atque ego inter caeteros. Huic igitur cum respondebo tuum quoque judicium opponam, quin imo et unicam progressionem abs te repertam 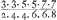&c. magno istorum molimini praeferre non verebor. Caeterum de lucubrationibus tuis ut quid sentiam penitius intelligas, videreris mihi haud exiguum fecisse operae praetium, etiamsi nihil praeter eam quam dixi progressionem attulisses, utique si vera est. Vellem autem ut vel ipse tu vel alius examen per numeros quod ego aliquousque perduxi ulterius prosequeretur, nam demonstrationes per inductionem quas adhibes, nondum tam perspicuae aut certae mihi videntur ut absque haesitatione illis confidere liceat. In propositione 191 non benè intelligo qua ratione ex eo quod β/α minor sit quam 2/1, conficias eandem β/α minorem esse quam 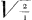. Itaque haec quaeso mihi explica, neque mirare quod adhuc ea non sim assecutus, cum uti dixi nuper admodum libros tuos acceperim. Lineam Curvam propositione 192 propositam non existimo te cuiquam pro geometrica approbaturum, nam quae geometricae sunt in ijs inter duo quaelibet data in ipsis puncta possunt quotcunque alia investigari, quod in tuis secus est. Neque ad determinationem sufficit quod adjunxisti, ut aequabilis sit, non hinc inde subsultans, quoniam et ex circumferentiae particulis tales componere licet, quae transeant per ea puncta quae in curva tua definita sunt. Quae de angulo contactus prolixe disputas in ijs plane tecum sentio, semperque visum est perperam ipsi affingi anguli nomen vel certe quantitatem.

De Conicis³⁾ Schotenius mihi scripsit⁴⁾ ea sibi perlecta esse atque admodum probari. ego vix inspicere coepi. animadverti tamen algebraicis demonstrationibus te uti, quae sane compendiosae sunt, optandumque esset ut ab omnibus intelligerentur. Ego ejusmodi demonstrationes nuper adhibui in tractatu quodam de aleae ratiocinijs, quem Schotenius una cum suis quae nunc edit operibus in lucem dare proposuit. Occasionem mihi dederant in Gallia Mathematici quidam, qui quaestiones hujusmodi mihi proposuerant. Nempe quoto jactu aliquis una tessera qualibus vulgo nunc utuntur, senarium se daturum contendere possit. item duabus

2) Voyez la ‘Dedicatio’ de l'ouvrage Arithmetica Infinitorum.

3) Voyez l'ouvrage cité dans la Lettre N^o. 286, note 2.

4) Voir la Lettre N^o. 313.

[p. 460]

tesseris quoto jactu senarios duos. et plurimas praeterea hujus generis, quibus resolvendis non admodum facile fuit prima principia reperire.

Saturnum ansas suas non recepisse vos quoque isthic procul dubio observasti. Vale.