Oeuvres complètes. Tome VI. Correspondance 1666-1669

[p. 328]

N^o 1689.
J. Gregory à [H. Oldenburg].
[25 Juin 1668].

La pièce a été imprimée dans les Philosophical Transactions No. 36, du 15 Juin 1668 [V. st.].

An Account

of a Controversy betwixt Stephano de Angelis, Professor of the Mathematicks in Padua, and Joh. Baptista Riccioli Jesuite; as it was communicated out of their lately Printed Books, by that Learned Mathematician Mr. Jacob Gregory, a Fellow of the R. Society.

Riccioli in his Almagestum Novum¹⁾ pretends to have found out several new demonstrative Arguments against the Motion of the Earth. Stephanus de Angelis, conceiving his Arguments to be none of the strongest, taketh occasion²⁾ to let the world see, that they are not more esteem'd in Italy, than in other places. Manfredi³⁾, in behalf of Riccioli, endeavours to answer the Objections of Angeli, and this latter⁴⁾ replyes to Manfredi's Answer. The substance of their discourse is this following.

Although the Arguments of Riccioli be many, yet the strenghth of them consists chiefly in these three:

1) Voir l'ouvrage cité dans la Lettre N^o. 280, note 7.

2) Consultez: St. de Angelis, Considerazioni (voir la Lettre N^o. 1575, note 2^b).

3) Consultez: M. Manfredi, Argomento fisico-mathematico (voir la Lettre N^o. 1575, note 2^e).

4) Consultez: St. de Angelis, Seconde Considerazioni (Voir la Lettre N^o. 1575, note 2^d).

The first.

Multa corpora gravia, dimissa per Aerem, in Plano Aequatoris existentem, descenderent ad Terram cum Velocitatis Incremento reali & notabili, & non tantùm apparenti. Sed si tellus moveretur motu diurno tantùm circa sui centrum, nulla corpora gravia, dimissa per Aerem, in Plano Aequatoris existentem, descenderent ad Terram cum velocitatis incremento reali ac notabili, sed tantùm cum apparenti. Ergo. Tellus aut non movetur, aut non movetur diurno tantùm motu.

The second.

Si Tellus moveretur motu diurno, aut etiam annuo, multò debilior esset ictus

[p. 329]

Globi bombardici explosi in Septentrionem aut Meridiem, quàm ab Occidente in Orientem. At consequens est falsum. Ergo. & antecedens.

The third.

Si Tellus diurna revolutione moveretur, Globus argillaceus unciarum 8. ex altitudine Romanorum pedum 240. per aerem quietum dimissus, obliquo descensu in Terram delaberetur absque incremento reali ac physico velocitatis, vel certè nunquam tanto, quanta est proportio percussionis ac soni per casum ex dicta altitudine facti. Sed posterius est absurdum. Ergo. et prius.

In Answer to the first of these Arguments, Angeli denieth the Minor, which Riccioli pretends to prove thus;

Si Tellus moveretur solo diurno motu, aliquod Grave, dimissum ex Turris vertice C in Plano Aequatoris existentis, describeret suo motu naturali portionem lineae CTI, quae esset ad omnem sensum circularis.

Vide Figuram I.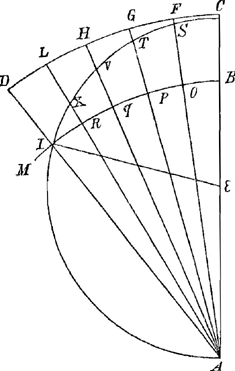

Fig. 1.

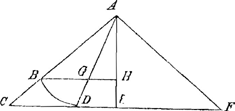Fig. 2.

This Angeli denies, shewing by Computation, that Riccioli his Observation proveth no such thing. For (saith Angeli) according to Riccioli, in one second of an hour the weight descends 15 foot; in 2 seconds, 60 foot; in 3 seconds 135 foot;

[p. 330]

and so continually the spaces from the beginning are in duplicate proportion of the Time from the beginning; and, according to the same Author, AB (the semidiameter of the Earth) is of 25870000 foot, and BC (the height of the Tower of the Asinelli in Bononia) of 240 foot; and therefore AC is 25870240, which hath the same proportion to FS, 15 foot, to wit, ye fall in one second, which AC in parts 20000000000 hath to FS 11596 54356/224189; but supposing, with Riccioli, CSIA a semi-circle, FS is 53 parts, of wich AC is 10000000000: Hence concludeth Angeli, that CSIA is no wayes near to a semi-circle; which is most sure, if so be the weight fall not to the Center of the Earth precisely in 6 hours: For, in this case of Riccioli, the weight falls to the Center of the Earth in 21 minutes and 53 seconds.

Manfredi in his Answer for Riccioli affirms, that Angeli understands not the Rule of Three, in giving out FS for 11596 54356/224189, of which AC is 20000000000: And Angeli in his Reply affirms his Analogy to be so clear, that there can be nothing said more evident than it self to confirm it; referring in the mean time the further determination to Geometers.

Angeli might have answer'd Riccioli's Argument, granting the weight to move equally in a semi-circle, by distinguishing his Minor thus;

Nulla Corpora gravia descenderent ad Terram cum velocitatis incremento reali ac notabili, si Velocitas computetur in circumferentia semi-circuli; Minor propositio est vera. At non computatur ita Motus descensivus: nam hic motus aequalis in circumferentia semi-circuli CIA. componitur ex motu aequali in quadrante CD, et motu accelerato in semidiametro mobili CA; & hic motus acceleratus in semidiametro est verus & simplex motus descensivus; in qua acceptione Minor propositio est falsissima, & Riccioli etiam experientiis contraria. But it seems, that Angeli answereth otherwise, to make Riccioli sensible, that CIA is no semicircle; concerning the nature of which Line they debate very much throughout the whole discourse.

The second Argument is much insisted upon by Angeli, to make his solution clear to vulgar capacities; but the substance of all is, That the Canon-ball hath not only that violent motion, impressed by the Fire, but also all these motions proper to the Earth, which were communicated to it by the impulse received from the Earth: for, the Ball, going from West to East, hath indeed two impulses, one from the Earth, and another from the Fire; but this impulse from the Earth is also common to the mark, and therefore the Ball hits the mark only with that simple impulse, received from the Fire, as it doth being shot towards the North or South; as Angeli doeth excellently illustrate by familiar examples of Motion.

To Riccioli his third Argument Angeli answereth, desiring him to prove the sequel of his Major, which Riccioli doeth, supposing the curve, in which the

[p. 331]

heavy body descends, to be composed of many small right lines; and proving, that the motion is almost always equal in these lines; and after some debate, concerning the equality of motion in these right lines, Angeli answers, that the equality of motion is not sufficient to prove the equality of percussion and sound, but that there is necessary also equal angles of incidence; which in this case he proveth to be very unequal. To illustrate this more, let us prove, that, other things being alike, the proportion of two percussions is composed of the direct proportion of their velocities, and of the direct proportions of the Sines of their angles of incidence. Supponamus autem sequens principium, nempe, quod percussiones (caeteris paribus,) sint in directa proportione cum velocitatibus, quibus mobile appropinquat planum resistens. Fig. 2^da. Sit planum CF, sintque duo mobilia omni modo aequalia, & similia, quae motu aequali accedant à puncto A ad planum CF, in rectis AD, AF: dico, percussionem in puncto D ad percussionem in puncto F esse in ratione composita ex ratione velocitatis in recta AD. ad velocitatem in AF, & ex ratione sinus anguli ADE ad sinum anguli AFE. Ex puncto A in planum CF, sit recta AE normalis, sitque recta AC aequalis rectae AF, & AB aequalis rectae AD, & planum BGH, parallelum plano CF: supponamus mobile, prioribus simile & aequale, moveri aequaliter in recta AC, eadem velocitate, qua movetur mobile in recta AD: quoniam plana BGH, CF, sunt parallela, & motus in recta AC est aequalis, igitur mobile eadem velocitate accedit ad planum BH, qua ad planum CF, & proinde percussiones in punctis B, C, sunt aequales, atque percussio in puncto D, est ad percussionem in puncto B, ut recta AE ad rectam AH, seu (ob aequales rectas AD, AB) ut sinus anguli ADE ad sinum anguli ABH, quod sic probo; velocitas mobilis in recta AD, est aequalis velocitati mobilis in recta AB, ipsi AD aequali, & ideo eodem tempore perficitur utraque recta AD, AB; & proinde eodem tempore perficiuntur accessiones ad plana resistentia AE, AH; ideoque velocitates accessionum ad plana resistentia sunt in directa ratione AE ad AH, atque ideò percussio in puncto D est ad percussionem in puncto C in eadem ratione AE ad AH; nempe ut Sinus anguli incidentiae ADE, ad sinum anguli incidentiae ACE, vel AFE. Quoniam autem rectae AC, AF, aequaliter inclinant ad planum CF, mobilia in reclis AC, AF, accedunt ad planum CF, in eadem proportione qua moventur in rectis AC, AF, & ideo percussio in C est ad percussionem in F in ratione velocitatis motus in AC seu in Ad ad velocitatem motus in AF; At demonstratum est antè, percussionem in puncto D ad percussionem in puncto C, esse in ratione sinus anguli ADE ad sinum anguli AFE, & nunc demonstratum est, percussionem in puncto C esse ad percussionem in puncto F, ut velocitas motus in AD ad velocitatem motus in AF. Igitur ex 5^a definitione 6ⁱ Elementorum, percussio in D, est ad percussionem in F, in ratione composita ex ratione sinus anguli incidentiae ADE ad sinum anguli incidentiae AFE, & ex ratione velocitatis in AD ad velocitatem in AF; quod demonstrare oportuit. Neminem moveat, quod haec demonstratio adstricta sit motibus aequalibus in lineis rectis & planis resistentibus;

[p. 332]

est enim vera in omni casu: nam, cum percussiones fiant in puncto, in hoc coincidunt rectum, curvum, aequale & inaequale; si autem in punctis percussiones non fiant, de illis non potest dari consideratio geometrica, sed judicandus est conclusionis defectus secundum defectum materiae à conditionibus requisitis, sicut semper fieri debet, dum demonstrationes geometricae corpori physico applicantur.

In Angeli his reply to Manfreddi, he maketh mention of an Experiment, which (as was related to him by a Swedish Gentleman) had been made with all due circumspection by Cartesius to prove the Motion of the Earth. The experiment was; He caused to be erected a Canon perpendicular to the Horizon; which being 24 times discharged in that posture, the Ball did fall 22 times towards the West, and only twice toward the East.