Oeuvres complètes. Tome II. Correspondance 1657-1659

N^o 582.
Christiaan Huygens à Fr. van Schooten.
7 février 1659.

La lettre se trouve à Leiden, coll. Huygens.
Fr. van Schooten y répondit par le No. 587.

Clarissimo Viro Domino Fr. Schotenio Chr. Hugenius S.

Post diutinum silentium à Milonio nostro literas¹⁾ accepi quibus istae quas tibi mitto inclusae erant. Mitto autem et demonstrationes ipsius²⁾, uti voluerat, circa Cycloidis lineae dimensionem, pulcerrimum illud Wrenni inventum, de quo proculdubio pridem intellexisti, nec non circa curvam quam olim Slusius nobis proposuerat. Sed et haec longè petita videtur, et illam de Cycloide multo quoque brevius jam diu absolvi, ita ut nihil opus haberem Theoremate illo Robervallij, quo Milonius utitur, aut ratione perturbata. Insuper et partes lineae dimensus sum, invento curvam M t semper duplam esse rectae c f, quam in schemate Miloniano³⁾ punctis signavi, nempe si tf fuerit parallela basi AL. Quae tamen non eò refero ut diligentiam studiumque viri mihi amicissimi apud te elevem, sed ut nostri quoque

1) Voir la Lettre N^o. 576.

2) Voir les Appendices N^os. 577 et 578.

3) Voir la figure de la Lettre N^o. 577.

[p. 344]

simul tibi rationem reddam. Si quando hîc te videre contigerit alia quoque quae de eadem curva investigavi tibi exhibebo, nempe qua ratione centrum gravitatis tum spacij ab ipsa comprehensi tum lineae ipsius ejusque partium repererim. In presentia illud tantum hîc adjiciam qualenam inventum meum fuerit circa parabolam, alteram eorum de quibus anno ab hinc et amplius te certiorem feci⁴⁾, sed unum



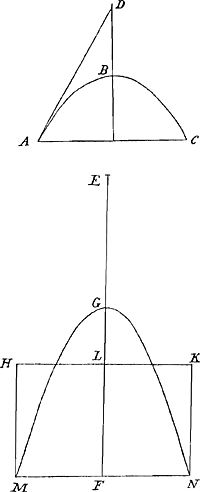duntaxat explicui, nempe de conoidis parabolici superficie. Quum verò illud quod hactenus penes me continui, etiam Auzotio obvenisse ex Milonij epistola intelligam⁵⁾, non ultra profecto premendum censeo: Atque equidem tale quid metuens opportunè admodum Domino Carcavio, ante hebdomadas aliquot illius copiam⁶⁾ feci. Est autem hujusmodi. Data parabolae portione recta, ABC, quam in termino basis contingat recta AD, axi producto occurrens in D; si statuatur recta EF dupla dictae AD; EG vero aequalis basi AC; describaturque hyperbola MGN, cujus dimidium latus transversum sit EG, diameterque à centro ad basin pertingens EF. ponatur verò portioni hyperbolicae MGN aequale esse parallelogrammum super eadem basi consistens, HN; cujus latus basi oppositum secet rectam EF in L. Dico abscindi rectam LE aequalem curvae parabolicae ABC. Unde vides etiam contra, si huic recta aequalis detur, hyperbolae portionem quadrari. De superficiebus sphaeroidum, et conoidis etiam hyperbolici, antehac puto tibi me descripsisse quae inveneram. Quod si secus fuerit mittam cum volueris. Aequum enim est, cum libris integris tua nobis inventa elargiaris ut etiam eorum in quae nos subinde incidimus particeps fias. Vale Schoteni Clarissime et Milonij demonstrationes ubi legeris quaeso mihi remitte. Scribe

4) Voir la Lettre N^o. 444.

5) Voir la Lettre N^o. 576.

6) Voir la Lettre N^o. 566.

[p. 345]

etiam an ex Gallia Huddenius jam reverterit. Epistolas ipsius editas⁴⁾ a Domino de Wit commodato accepi in quibus praeclara multa.

7 Febr. 1659.

4) Nous n'avons pu trouver cette édition de Lettres de J. Hudde.