Oeuvres complètes. Tome II. Correspondance 1657-1659

[p. 337]

N^o 578.
Cl. Mylon à Christiaan Huygens.
juin 1658.
Appendice II au No. 576.

La pièce se trouve à Leiden, coll. Huygens.

La Quadrature des Perles. de Monsieur Sluse, par Cl. Mylon. En Juin 1658.

Si la Courbe A C h b K, à cette proprieté. A b estant son Axe, C d, hg, ses ordonnées. si C d est à h g comme le produit de A d en d b quarré au produit de A g en gb quarré. Je Dis que l'Espace plan A C h b A, est au rectangle de l'axe A b et de l'ordonnée du milieu h g, comme 2. à 3.

Soient diuisées A g, gb en nombre egal et jndefini de parties egales aux points comme d. d'ou soient esleuées autant d'ordonnées d C.

A Cause de la proportion enoncée par l'hypothese, quand la somme des ordonnées d C (ou son homologue, la somme des produits A d en d b quarré) representera l'espace plan A C h b A; Alors la somme d'autant de fois h g l'ordonnée du milieu (ou son homologue, la somme des produits A g en g b quarré c'est a dire des A g Cubes) representera le rectangle AI.

Or les produits A d en d b quarré de suite sont les produits des termes qui sont vis a vis l'un de l'autre dans les deux progressions E, F, dont E contient les Nombres naturels depuis l'vnité jusques au plus grand nombre de la diuision jndefinie de A b, et la Colonne F contient leurs quarrez Naturels de suite d'un ordre retrograde.

Je separe ces produits et en faits les Colonnes O, P, Q, R, S, T, U, X. dont chaque nombre est le produit de l'vnité par chaque nombre de la progression F. ainsi en la Colonne O. le Nombre 64 est le produit de 1. en 64. et aux Colonnes O, P, les nombres 49. sont les produits de 1. en 49. et de 1 en 49 et ainsi de suite.

Alors chaque Colonne O, P, Q, R,¹⁾ T, U, X, sera composée d'vne suite retrograde des quarrez Naturels en descendant toujours d'un moins.

Donc les nombres de chaque Colonne O, P, Q, R, S, T, U, X, estant assembles, sont le tiers d'autant de fois le plus grand nombre de la mesme Colonne par la doctrine des Infinis. car la somme des quarrez est le tiers d'autant de fois le plus

1) Ajoutez: S.

[p. 338]

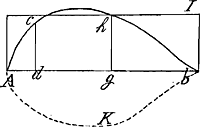
grand quarré. Et partant la somme de toutes ces Colonnes O, P, Q, R, S, T, U, X estant 2. la somme d'autant de fois leurs grands Nombres sera 6.

Mais chaque somme d'autant de fois le plus grand nombre en chaqu'une de ces Colonnes O, P, Q &caet. est vn plus grand Cube, et toutes ces sommes du plus grand Cube de suite depuis X jusques a O seront la suite des Cubes naturels depuis l'vnité jusques au plus grand de la diuision jndefinie. Et la somme de tous ces Cubes de suite est le quart d'autant de fois le plus grand, c'est a dire le quart du quarréquarré du plus grand nombre de la diuision jndefinie, par la doctrine des Infinis. donc ce plus grand quarréquarré sera 24.

Or la somme d'autant de fois Ag Cube qui est la huitieme partie d'autant de fois le plus grand Cube A b, (c'est a dire la huitieme partie de Ab quarréquarré) est 3.

Donc la somme de toutes ces Colonnes O, P, Q, R, S, T, U, X, c'est a dire des solides A d en d b quarré, c'est a dire l'Espace plan A C h b A, estant 2. la somme d'autant de fois A g en g b quarré, c'est a dire son homologue le rectangle AI est 3. donc jls sont entr'eux, comme 2. a 3. ce qu'il falloit demonstrer.

Corollaire.

Par vne semblable methode on trouuera la quadrature de la perle en laquelle l'ordonnée C d est a l'ordonnée h g comme A d en d b Cube à A g en g b Cube, car la figure A C h b A sera au ▭ A I comme 8. a 10. ou comme 4. a 5. en faisant vne semblable construction en laquelle les Colonnes O, P, Q, R &caet. contiendront les Cubes naturels.

Et ainsi des autres perles a l'Infiny.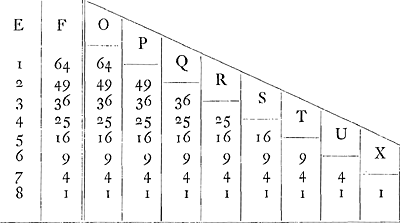