Oeuvres complètes. Tome II. Correspondance 1657-1659

N^o 577.
Cl. Mylon à Christiaan Huygens.
26 janvier 1659.
Appendice I au N^o. 576.

La pièce se trouve à Leiden, coll. Huygens.

Propositio Domini Wren Angli. Demonstrata a Claudio Mylon die 26. Januarii 1659.

Cyclois quadrupla est diametri Circuli genitoris.

Diuidatur semicirculus primus Abc jn partes aequales jnter se, numero verò jndefinitas vt jn b. f &caet et à punctis diuisionum b, f, ducantur totidem rectae b I, f t basi LA parallelae vsque ad Cycloidem jn I et t. tum ab jisdem punctis b ducantur aliae b E retro circulum tangentes, quae fiant singulae aequales arcui jntercepto b f. sumantur jn singulis b I rectae b h aequales rectae b E, et compleantur totidem Rhombi h E, quorum ducantur Diametri b g, siantque rectae IK parallelae singulae singulis b g correspondentibus. Patet ex doctrina motuum compositorum, rectas IK tangere Cycloidem jn punctis I. sumantur IK singulae aequales correspondentibus bg.

facillimé demonstrabitur angulos b h g ab A jncepiendo per singula diuisionis puncta b, f et aliis vsque ad C, crescere (?) quantitate anguli diuisionis ad cen-

[p. 336]

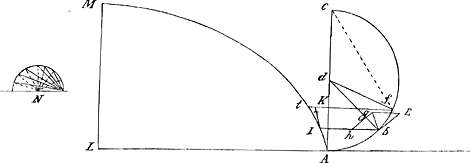
trum dbf. quare singulae rectae bg erunt Chordae semicirculi (vt in figura N) radio h b descripti et jn totidem partes diuisi jn quot diuisus est semicirculus A b c.

Manifestum quoque est summam tangentium b E aequalem esse semircircumferentiae A b c, quia singulae b E singulis arcubus diuisionis b f positae sunt aequales.

Sed et rectae IK Cycloidem tangentes vt jn I, aequales quoque sunt portionibus Cycloidis I t quae jpsis sunt contiguae. Nam ob diuisionem semicirculi A b c jndesinitam, portiones Cycloidis jnter duas proximas parallelas b I, f t jnterceptae, recté sumuntur pro Lineis rectis crescentibus ab A per I, t, vsque ad M, similiter ac crescunt jpsae tangentes IK, si quidem motus puncti I Cycloidis portionem I t describentis, aequalis est motui ejusdem puncti I, rectam IK eodem tempore percurrentis. hoc que facilé concedetur ab jis qui doctrinae Jndiuisibilium et motuum compositorum non sunt Ignari.

Quare omnes tangentes IK simul sumptae aequales sunt semicycloidi A I M.

Est ergo semicircumferentia A b c ad semicycloidem AIM, vt summa tangentium b E ad summam tangentium I K. siue vt radius h b indefinitè sumptus ad summam Chordarum semicirculi jndefinitè diuisi, vt jn figurâ N. siue vt radius rotae Ad toties sumptus ad summam Chordarum semicirculi A b c.

Sed summa Chordarum semicirculi A b c aequalis est duplae summae sinuum rectorum quadrantis ejusdem rotae jn totidem partes jndefinitè diuisi, jn quot nempè semirota A b c diuisa est.

Et Radius est ad Quadrantem (siue diameter AC est ad semicircumferentiam Abc) ut summa sinuum rectorum ejusdem quadrantis, ad duplum¹⁾ radii Ad toties sumpti. quod facilè demonstrabitur. et hoc quidem jam pridem a Roberuallio demonstratum est. Quare ex aequo et jn ratione perturbatâ. Diameter AC est ad semicycloidem AIM, vt Radius Ad jndefinities sumptus, ad duplum ejusdem radii A d toties sumpti hoc est vt 1. ad 2.

Igitur jntegra Cyclois est Quadrupla diametri AC quod erat demonstrandum.

Diameter AC

Semicircumferentia A B C

Semicyclois A I M

Radius jndefinitè A d

Summa chordarum siue dupla summa Sinuum quadrantis

^2) Duplum radii A d jndefinitè.

1) Mylon s'est mépris: il faut ôter le mot ‘duplum’; ce qui naturellement est d'influence sur la suite du raisonnement, mais le résultat reste correct.

2) Ce dernier tableau semble contenir une proportion continue: seulement les trois derniers termes devraient être un peu changés. En effet, on démontre la proposition suivante:
AC: ABC: AIM = Summa Sinuum quadrantis: Radius indefinité Ad: Dupla Summa Sinuum quadrantis.