Oeuvres complètes. Tome I. Correspondance 1638-1656
(1888)–Christiaan Huygens–
[pagina 519]
| |
No 356.
| |
[pagina 520]
| |
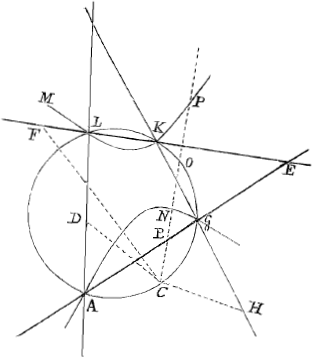
caeteris duxi. Vocentur autem hae Priores brevitatis gratia, reliquae vero duae Posteriores, quoniam crebra ipsarum mentio facienda erit. In fig. 2daGa naar voetnoot2) exemplum
 dedi, ubi locus puncti C Parabolam contingit NAGC, et praeterea sectiones oppositas GC, AO. Hic autem ex C in positione datas omnes lineae ad rectos angulos ducuntur, invenieturque semper rectangulum sub CB, CF aequale rectangulo sub CH, CD. Dantur hic inter se parallelae AB, una posteriorum et ED una priorum, reliquae vero duae in ipsa AB sese intersecant, et sic quidem ut AE sit aequalis AG. Hujus casus constructionem ex calculo inquisivi, quem hic subjicere non pigebit. Sit BD distantia parallelarum ∞ a, AB ∞ x, BC ipsi AB perpendicularis ∞ y. sumo autem AB ejus longitudinis ut BC intret angulum DGQ, quoniam intra hunc angulum primo mihi punctum C indagandum propono. | |
[pagina 521]
| |
Est igitur CD ∞ y - a Ratio data AB ad BQ. AB, BQ vel BR  Vides ex aequatione punctum C contingere parabolam. Quae quidem ex Cartesij praescripto sic construetur. Sit KI aequalis et parallela AB, et abscindat BK aequalem ¼ a hoc est ¼ BD. Porro eadem producatur ad N ut sit IN ∞ 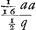 sive ⅛ aa/q, et erit N vertex parabolae. latus verò rectum ∞ ½ q. sive ⅛ aa/q, et erit N vertex parabolae. latus verò rectum ∞ ½ q.
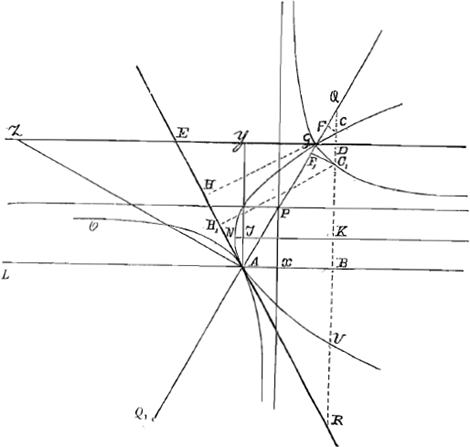
Si ducatur AY perpendicularis in EG et AZ perpendicularis in AG, fit ZY ∞ q et YG ∞ aa/q. Quaeratur jam punctum C1 intra parallelas AB, ED positis rursus AB ∞ x, BC1 ∞ y. Et invenientur eadem qua prius methodo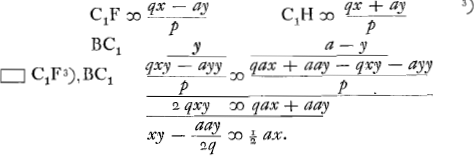 Ga naar voetnoot3) | |
[pagina 522]
| |
Haec aequatio ostendit punctum C1 contingere hyperbolem per ea quae tradidit in Commentarijs suis Florimond de BeauneGa naar voetnoot4), est enim similis casui ipsius quarto, ubi xy - cy ∞ bx. Et asymptotae secundum ipsius regulam inveniantur sumpta AX ∞ ½ aa/q et XP parallela BC et ∞ ½ a. nam haec una est ex asymptotis, altera quae per P ipsi AX parallela ducitur. Puncta vero in hyperbolis data sunt A et G, unde facile est ipsas describere. Vides hic ex priori aequatione esse y aequalem BC vel BNGa naar voetnoot5) at ex posteriori aequatione etiam BC1 proposito satisfacere, licet ea ex priori aequatione non fuerit inventa. quod tamen nequaquam mirandum est ut postea intelliges. Quod si lineae positione datae AG, AE ita secuissent parallelas AB, ED ut AG minor fuisset quam AE, caeteris positis ut prius, loco paraboles VAG alia hyperbole haberetur, cujus opposita etiam proposito satisfecisset, sitaque fuisset alicubi intra angulum QALGa naar voetnoot6) ita ut nullam linearum positione datarum secaret contingeretve. Angulis autem AEG, AGE aequalibus existentibus, etiamsi intersectio duarum EA, GA, non incidat in rectam AB, vel EG, semper parabola invenietur. Porro in universum sciendum est, quoties in datas positione quatuor rectas ex puncto uno rectae ducuntur in datis angulis, estque quod sub duabus earum continetur, aequale ei quod sub duabus reliquis, vel ad hoc datam rationem habens; semper per unamquamque intersectionem unius priorum cum una posteriorum duos locos transire (loci nomine etiam rectam lineam intelligendo). Quod siquae hyperbole fuerit ejus oppositum quoque punctum illud continget. Atque ita locus puncti semper erunt duae coni sectiones integrae: hoc est, quas in oppositis conis unius plani intersectio vel contactus efficit. nam aliquando etiam una linea recta pro integra coni sectione venit, velut in figura 3a ubi bina sunt parallelarum paria sese intersecantia. Ibi enim locus puncti est ad sectiones oppositas AC, BD, et praeterea ad rectam AB. Ponendo videlicet omnes ex puncto in datas positione perpendiculares duci, vel certe in ijsdem omnes angulis. Venio nunc ad solutionem dubij illius vel difficultatis quae inde suboritur quod non statim intelligamus qui fiat ut cum aequatio duas tantum dimensiones preferat, tres tamen quatuorve lineae sint proposito utiles, quasi plures duabus radicibus continent. Qua in re sciendum est nequaquam lineas omnes quae problema aliquod efficiant semper nobisGa naar voetnoot7) Primo comperi id non tantum in hujusmodi locorum quaestione ita se habere sed in alijs quoque problematis. Exempli causa si oporteat rectam interminatam | |
[pagina 523]
| |
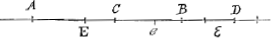 AD ita secare in puncto E ut è rectis ad data in ipsa quatuor puncta A,B,C,D absumtis, rectangulum sub duabus EA, EB, comprehensum aequetur rectangulo sub duabus EC, ED. Sit AC partium 5; CB 4; BD 3; Et ponatur AE ∞ x sumpto puncto E inter A,C. fit igitur EB ∞ 9 - x. EC ∞ 5 - x, et ED ∞ 12 - x. 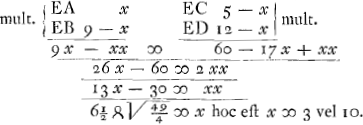 Haec aequatio ostendit punctum ε dupliciter accipi posse, ut proposito satisfiat, nimirum vel inter AC vel inter BD. Atqui etiam tertius locus est puncti ε inter C et B si nimirum sumatur Ae ∞ 7½: quod tamen ex aequatione praecedenti nequaquam resciri potest. Nec sane videtur mihi W. SnelliusGa naar voetnoot8) hoc considerasse in restitutione Apollonij de Sectione determinataGa naar voetnoot9). Sed quaenam hic causa subest dices, quare non omnes diversas magnitudines radicis x aequatio nobis exhibet? Nempe haud alia quam quod plus in propositione complectimur quam una aequatione explicari potest. Quaerendum namque est punctum ε etiam inter C et B, orieturque alia aequatio quae doceat Ae aequalem esse 7½. Cur autem plus in propositione ista complexi fuerimus, non adeo perspicuum est,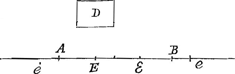 at magis in sequenti quaestione. Oporteat rectam interminatam AB secare in puncto E, ut quod fit rectangulum sub rectis ad data duo in ipsa puncta A, B, absumptis, dato spatio D aequale sit. quod sit minus quarta parte quadrati AB. Sit AE ∞ x. Et hic quidem facile intelligis quadrifariam accipi posse punctum E, ut semper problema efficiat cum tamen aequatio quadrata duas tantum quantitates radicis x ostensura sit, utramque veram (ut vocare solemus) cum inter A, B punctum E quaeretur; alteram vero duarum falsam alteram veram si ultra A vel ultra B quaera- | |
[pagina 524]
| |
tur. Adeo ut binis saltem aequationibus necesse sit inquirere punctum ε. Hoc autem merito evenire liquet, quoniam per rei naturam fieri non potest, ut quod in propositione est una aequatione comprehendatur. debuisset enim hoc tantum proponi quomodo linea AB inter A, B interjecta secanda esset ut rectangulum sub partibus spatio D aequale esset. Et rursus quomodo extra puncta AB secanda esset ut quod sub tota et parte adjecta et sub adjecta datum spatium aequaret. Haec vero utraque simul una propositione continebantur, quae proinde exuberabat. Et plane idem in Problemate loci ad 4 lineas contingere necesse est dum nunc in hoc nunc in alio angulo punctum C quaeritur. licet non tam facile possit perspici. Hisce rationibus mihi quidem satisfeci admirationemque omnem exemi. quibus si tu quoque assenseris Vir Clarissime, recte opinor facies, si in commentarijs tuis iterato prodituris eorundem mentionem aliquam facias omnemque hanc de duplici loco contemplationem sed accuratius quam a me factum vides lectoribus tuis exponas. Epistolam MilonijGa naar voetnoot10) tibi remitto, ex qua demonstrationem Robervalli egregiam sane de Trianguli sphaerici superficie excerpsi. Altera de Parabolicae lineae comparatione cum helice Archimedis non aeque certa est. At mihi magnus Geometra erit qui vere Geometricam demonstrationem hic excogitaverit, nam propositio quidem vera est ut opinor, et pridem mihi quoque occurrerat. Domino Kechelio librum tuum brevi remittam, cumque isthuc excurrero, coram ipsi gratias agam. |
|