Oeuvres complètes. Tome I. Correspondance 1638-1656

N^o 355.
G.P. de Roberval à Cl. Mylon.
Appendice II au N^o. 353.

La copie se trouve à Leiden, coll. Huygens.

Propositio.

Ratio maximi in sphaera circuli ad superficiem trianguli sphaerici, eadem est quae duorum angulorum rectorum ad differentiam sive excessum quo tres anguli trianguli sphaerici superant duos rectos.

[p. 518]

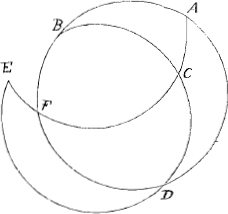Sit triangulum sphaericum BAC, dico &c. Producantur latera BA, BC donec concurrant in D. Et AC productum occurrat quidem ipsi BA in F, ipsi vero BCD in E. Est igitur BADCB sector sphaerae: item ACFBA, item CDEFC. Estque superficies sectoris BADCB ad superficiem sphaerae ut angulus CBA ad quatuor rectos.^a) Similiter superficies sectoris ACFBA ad superficiem sphaerae, ut angulus BAC ad 4 rectos. Et denique sectoris CDEFC superficies ad superficiem sphaerae ut angulus FCD vel BCA ad 4 rectos. Trium autem horum sectorum superficies simul aequantur superficiei hemisphaerij BADF, una cum duobus triangulis BAC et FDE, hoc est una cum triangulo BAC bis sumpto; nam triangulum FDE triangulo BAC aequale est et simile, ut postea ostendetur. Ergo componendo, erit summa trium sectorum, hoc est, superficies hemisphaerij BADF cum trianguli BAC duplo ad superficiem sphaerae, ut anguli B, A, C simul sumpti ad 4 rectos; vel sumpto consequentium dimidio, erit superficies hemisphaerij BADF una cum duplo triangulo BAC ad ipsam hemisphaerij superficiem ut anguli B, A, C, simul sumpti ad 2 rectos. Et dividendo, duplum triangulum BAC ad superficiem hemisphaerij, sicut excessus angulorum B, A, C, supra duos rectos ad duos rectos. Et sumtis semissibus utriusque terminorum antecedentium; triangulum BAC ad maximum sphaerae circulum (per demonstrata ab Archimede), sicut excessus angulorum B, A, C supra duos rectos ad duos rectos. quod erat demonstrandum.

Quod autem triangulum BAC sit aequale triangulo DFE sic ostenditur.

Angulus E aequalis est opposito ECD, ex Theodosio¹⁾. hoc est ACB. Similiter angulus EDF aequalis est ipsi ADC, hoc est, ABC. denique angulus EFD aequalis BFC, hoc est, BAC. Cum igitur omnes anguli omnibus aequales sint in triangulis BAC, DFE ipsa quoque triangula aequalia erunt.

Potuisset etiam laterum aequalitatem demonstrasse omissis angulis.

Nam quia BAD est semicirculus, itemque ADF, dempto arcu communi AD erit arcus BA aequalis DF. Sic quoniam BCD et CDE sunt semicirculi dempto communi CD erit BC aequalis DE. Eademque ratione AC aequalis FE^b).

a) Nonnulla inter describendum immutavi. [Mylon.]

1) Theodosii Tripolitae Sphaericorum Libri III. A Christophoro Clavio Bambergensi Societatis Iesv, perspicvis demonstrationibvs, at scholijs illustrati. Item Eiusdem Christophori Clavii Sinvs. Lineae Tangentes et Secantes. Triangvla rectilinea atqve sphaerica. Romae. Ex Typographia Domini Basae. m.d.lxxxvi. Permissv Svperiorvm. in-4^o.

b) Monsieur de Roberval m'a dit qu'il avoit trouuè la raison de toute portion de superficie sphaerique au grand cercle de la sphere. Il ne nous l'a pas encore communiquè. [Mylon.]