Oeuvres complètes. Tome I. Correspondance 1638-1656
(1888)–Christiaan Huygens–No 223.
| |
[pagina 330]
| |
lineas attinent. Equidem non multo meliora Gregorianis à novo hoc Cyclometra expecto, sed tamen videndum. Domini Ordines quid statuerint circa Examen tuum meumve, non comperi. Veruntamen quia ne verbum quidem renunciari mihi aut gratias agi voluere, dabo operam ut resciscam quo consilio id fecerint. Cardani regularum inventio per Algebram nostram, quam tantopere exponi tibi desideras, ea est hujusmodiGa naar voetnoot3). Proponatur aequatio x3 ∞ - px + q, hoc est, x3 + px - q ∞ o sitque invenienda quantitas x. Augeatur radix quantitate aliqua incognita z ut sit x + z ∞ y, hoc est x ∞ y - z. Ergo x3 ∞ y3 - 3yyz + 3yzz - z3 et loco prius expositae aequationis quae erat x3 + px - q ∞ o erit ista y3 - 3yyz + 3yzz - z3 + py - pz - q ∞ o. Hic quoniam - 3yyz + 3yzz fit ex ductu y - z in - 3yz; et rursus quod habetur + py - pz fit ex y - z in + p, apparet quod si 3yz sit ∞ p, tum se mutuo tollent dicti termini - 3yyz + 3yzz et + py - pz, solique restabunt y3 - z3 - q ∞ o. Sit igitur 3yz ∞ p. Ergo z ∞ ⅓ p/y. Et aequatio erit y3 - 1/27 p3 / y3 - q ∞ o. Unde y6 ∞ qy3 + 1/27 p3, quae quadrata aequatio est, fitque y3 ∞ ½ q +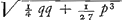 . Quare y ∞ . Quare y ∞ 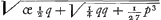 . Cognita jam quantitate y non ignorabitur z, quae erat ∞ ⅓ p/y. Erat autem x ∞ y - z. Ergo . Cognita jam quantitate y non ignorabitur z, quae erat ∞ ⅓ p/y. Erat autem x ∞ y - z. Ergo

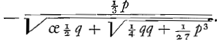 Quae regula facilior videri possit quam Cardani illa, quoniam semel tantum radicem cubicam extrahere opus sit. Caeterum ut ipsam Cardani regulam exhibeamus, quantitatem z similiter ut y ex praecedentibus inveniemus. Nimirum ex eo quod ponebatur 3yz ∞ p fit y ∞ ⅓ p/z. Unde loco superioris aequationis y3 - z3 - q ∞ o erit 1/27 p3 / z3 - z3 - q ∞ o. hoc est z6 ∞ - qz3 + 1/27 p3. Unde z ∞
Quae regula facilior videri possit quam Cardani illa, quoniam semel tantum radicem cubicam extrahere opus sit. Caeterum ut ipsam Cardani regulam exhibeamus, quantitatem z similiter ut y ex praecedentibus inveniemus. Nimirum ex eo quod ponebatur 3yz ∞ p fit y ∞ ⅓ p/z. Unde loco superioris aequationis y3 - z3 - q ∞ o erit 1/27 p3 / z3 - z3 - q ∞ o. hoc est z6 ∞ - qz3 + 1/27 p3. Unde z ∞  . Cum itaque fuerit x ∞ y - z. Erit jam x ∞ . Cum itaque fuerit x ∞ y - z. Erit jam x ∞ 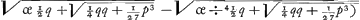 . Quae Cardani regularum una est. Altera simili methodo invenitur in hunc modum. Detur x3 ∞ px + q, sive x3 - px - q ∞ o. Diminuatur radix quantitate incognita z, ut sit x - z ∞ y, hoc est, x ∞ y + z. Eritque prioris aequationis loco ista y3 + 3yyz + 3yzz + z3 - py - pz - q ∞ o. Hic rursus si ponatur 3yz ∞
p, tollent se mutuo quantitates istae + 3yyz + 3yzz et - py - pz, tantumque supererunt y3 + z3 - q ∞ o. Sit ergo 3yz ∞ p, hocGa naar voetnoot4) . Quae Cardani regularum una est. Altera simili methodo invenitur in hunc modum. Detur x3 ∞ px + q, sive x3 - px - q ∞ o. Diminuatur radix quantitate incognita z, ut sit x - z ∞ y, hoc est, x ∞ y + z. Eritque prioris aequationis loco ista y3 + 3yyz + 3yzz + z3 - py - pz - q ∞ o. Hic rursus si ponatur 3yz ∞
p, tollent se mutuo quantitates istae + 3yyz + 3yzz et - py - pz, tantumque supererunt y3 + z3 - q ∞ o. Sit ergo 3yz ∞ p, hocGa naar voetnoot4)
| |
[pagina 331]
| |
est z ∞ ⅓ p/y. Ergo aequatio erit y3 + 1/27 p3 / y3 - q ∞ o. Unde y6 ∞ qy3 - 1/27 p3. Cujus aequationis ambigua est radix. Fit nimirum y ∞ 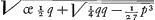 vely y ∞ vely y ∞ 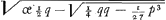 . Quod si porro quaeratur etiam z ex eo quod 3yz ∞ p, uti in prioris regulae inventione quaesita fuit, rursus ambigua radix aequationis invenietur, utque modo y ita nunc erit z ∞ . Quod si porro quaeratur etiam z ex eo quod 3yz ∞ p, uti in prioris regulae inventione quaesita fuit, rursus ambigua radix aequationis invenietur, utque modo y ita nunc erit z ∞ 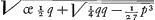 , vel z ∞ , vel z ∞ 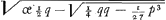 . Itaque alteram radicem sumendo pro z alteram pro y, (etenim ponendum est alteram altera majorem esse) fiet y + z, hoc est, x ∞ . Itaque alteram radicem sumendo pro z alteram pro y, (etenim ponendum est alteram altera majorem esse) fiet y + z, hoc est, x ∞ 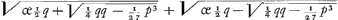 . . |
|

