Oeuvres complètes. Tome I. Correspondance 1638-1656
(1888)–Christiaan Huygens–
[pagina 213]
| |
No 147.
| |
[pagina 214]
| |
ende komt 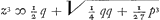 ende ende 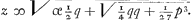 waer door z bekent zynde, soo is wederom bekent x die is z - ⅓ p/z. maer om dat x is ∞ z - ⅓ p/z, so is zx ∞ zz - ⅓ p en om dat x oock is ∞ ⅓ p/y - y, soo is yx ∞ ⅓ p - yy. Ergo gelijck bij gelijck geaddeert komt zx + yx ∞ zz - yy en dividerende door z + y, komt x ∞ z - y dat is waer door z bekent zynde, soo is wederom bekent x die is z - ⅓ p/z. maer om dat x is ∞ z - ⅓ p/z, so is zx ∞ zz - ⅓ p en om dat x oock is ∞ ⅓ p/y - y, soo is yx ∞ ⅓ p - yy. Ergo gelijck bij gelijck geaddeert komt zx + yx ∞ zz - yy en dividerende door z + y, komt x ∞ z - y dat is 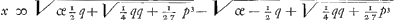 .
Om den anderen regel te vinden te weten als gegeven is x3 ∞ px + q zij gestelt x ∞ y + ⅓ p/y, ende werckende als voren komt y6 ∞ qy3 - 1/27 p3 alwaer y3 twee verscheijde quantiteijten ende daerom .
Om den anderen regel te vinden te weten als gegeven is x3 ∞ px + q zij gestelt x ∞ y + ⅓ p/y, ende werckende als voren komt y6 ∞ qy3 - 1/27 p3 alwaer y3 twee verscheijde quantiteijten ende daerom 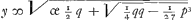 'twelck ick noemen sal a of oock 'twelck ick noemen sal a of oock 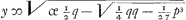 't welck ick sal noemen b. Ergo sal x sijn ∞ a + ⅓ p/a ende oock x ∞ b + ⅓ p/b 't welck ick sal noemen b. Ergo sal x sijn ∞ a + ⅓ p/a ende oock x ∞ b + ⅓ p/b
Ergo a x ∞ aa + ⅓p en b x ∞ bb + ⅓p en, gelijck van gelijck aftreckende komt ax - bx ∞ aa - bb en dividerende aen weder zijde door a - b komt x ∞ a + b dat is 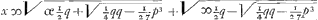 . .
Dit is voor soo veel aengaet de Regulen van Cardanus. Indien VE noch niet gevonden en heeft door wat middel men soude konnen geraecken tot die van des Cartes, dewelcke in plaets vande aequatie x4. pxx. qx. r stelt y6 + 2py4 + ppyy - qq ick sal het selve mede geerne aen VE communiceren. In het doorreijsen heb ick laestmael Professor Schooten de difficulteyt voorgestelt van de Cromme linie van des Cartes, hoe dat de selve in 6 plaetsen van een circel soude konnen doorsneden werden. de welcke mij tot antwoort seijde sulx eertijts beproeft ende waer bevonden te hebben. VE kan 'tselve mede lichtelijck examineren, stellende een aequatie inde welcke x 6 verscheijde waere quantiteyten beteyckent, als 1, 2, 3, 4, 5, 6. dat is x - 1 ∞ 0, item x - 2 ∞ 0 ende so voorts, ende alles door malkander multiplicerende. alhoewel ick meijn dat men sommighe der intersectien quaelijck moet konnen bemercken. Hier mede eijndigende en verwachtende met VE antwoort de demonstratie waer van geseijt was, blijve
Mijnheer VE dienstwilligen |
|


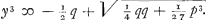 ende
ende
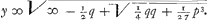 .
.