Oeuvres complètes. Tome I. Correspondance 1638-1656

N^o 144.
Christiaan Huygens à Fr. van Schooten.
26 decembre 1652.

La lettre et la minute se trouvent à Leiden, coll. Huygens.
Van Schooten y répondit par le No. 149.

Clarissimo Viro Domino Francisco à Schoten Christianus Hugenius S.

Ecce remitto tibi literas Domini Wallis¹⁾ quas ante biduum mecum me ferre voluisti, ut Problema quod de Linea Curva proposuit accuratius perpenderem. Feci id

1) On retrouve cette courbe dans une correspondance avec Wallis en 1655.

[p. 209]

quidem diligenter, et videtur sic responderi posse. Nimirum non cujusvis naturae lineas curvas existere, et hanc quam fingit planè esse impossibilem; quod facile est ostendere. Ponit siquidem lineam curvam AC quae istam habeat proprietatem, ut sumptis quotcunque partibus aequalibus in recta AT quae ab extremo axis AX perpendicularis exit, ductisque secundum acceptas partes lineis axi AX parallelis et in curva proposita terminatis, ut sit, inquam, ea quae ab axe prima est partis 1, qualium



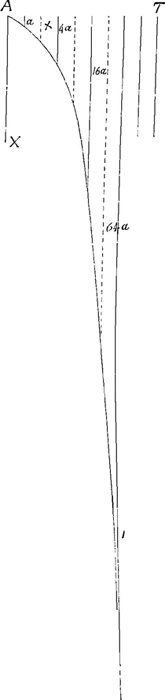tertia est 6, quinta 30, septima 140, nona 630, atque aliae deinceps tot partium quot obveniunt ex progressione quam statuit. Si igitur talis naturae est haec linea eaedem illae linearum proportiones contingerent, etiamsi ab initio partes majores in perpendiculari AT fuissent sumptae, sicut in parabola et alijs multis curvis haec se habere constat. Ponantur partes eae triplo majores sumptae; hoc est, pro prima linearum parellelarum sumatur quae fuit tertia, et consequenter pro tertia quae fuerat nona, et pro quinta quae fuisset decima quinta. Quia igitur prima nunc est partium 6, debebit tertia esse partium 36, ut locum habeat proportio 1, 6, 30, 140 &c. Sed tertia quae prius erat nona est partium 630. Ergo 630 aequalia 36. Quod est absurdum. Quare patet lineam ejus proprietatis nullam dari. Quod si quis à principio lineam curvam non ponat, sed ductis lineis aequidistantibus ut prius, faciat primam partis unius, tertiam 6, quintam 30 &c. et per harum terminos curvam quandam ducat ex vertice A, quaeratque longitudines 2^dae, 4^tae, 6^tae &c. dicendum est eas determinatas non esse, quia diversae lineae curvae per puncta ista duci possunt, etiam quae ad easdem partes cavae sint. Porro cum arithmeticè idem problema proponit Dominus Wallis et in serie numerorum crescentium 1, 6, 30, 140, 630 &c. quaerit, numeros interjiciendos inter binos quosque additum oportuit quâ conditione interjectos velit. Nam si simpliciter interjiciendos quaerit, possunt quilibet numeri interjici, si tantum praecedente majores et consequente minores sumantur ut 3, 16, 50 &c. vel 2, 8, 100, 300. At si tales interjiciendi quaeruntur, ut interjectorum primus, 3^tius 5^tus 7^tus eodem modo se habeant ut 1, 6, 30, 140 &c. quod sanè exigere ipsum existimo^a), tum rursus ad impossibile deveniemus. Nam cum primus interjectorum debeat minor esse quam 6, erit interjectorum tertius minor quam 36, quintus minor quam 180, sed quintus interjectorum est qui cadit inter 630 et 2772. Ergo jam turbata erit series

a) Inspice figuram in Epistola Domini Wallisii [Chr. Huygens].¹⁾

1) La figure de la page précédente a été copiée de la minute; dans la lettre même elle est indiquée seulement par ce renvoi. Elle répresente la Logarithmique, non pas la courbe, dont il est question ici (voir la figure page 217) et dont les ordonnées sont pour x = 1 , 2 , 3 , 4 y = 1 , 6/1 , 6/1 10/2 , 6/1 10/2 14/3

[p. 210]

numerorum crescentium. atque ita patet conditionem adjectam impossibilem fuisse; quod etiam eâ ratione ostendi poterat, qua paulo ante in linea curva usi sumus. Haec sunt quae in praesentia mihi occurrunt, quibus te assensurum opinor. Vale.

Hagae 26 Dec. 1652.

1) La figure de la page précédente a été copiée de la minute; dans la lettre même elle est indiquée seulement par ce renvoi. Elle répresente la Logarithmique, non pas la courbe, dont il est question ici (voir la figure page 217) et dont les ordonnées sont pour x = 1 , 2 , 3 , 4 y = 1 , 6/1 , 6/1 10/2 , 6/1 10/2 14/3