Oeuvres complètes. Tome I. Correspondance 1638-1656

N^o 164.
Christiaan Huygens à Fr. van Schooten.
[octobre 1653.]¹⁾

La minute et la copie se trouvent à Leiden, coll. Huygens.

Haec universalis est Problematis Constructio. Verùm si fuerit AQ minor quam AG. centro A radio AG circulus describatur inque eo ponatur GK aequalis duplae EG inventae ut prius. et diviso arcu reliquo GHK in tria aequalia ponatur subtensae partis unius GH aequalis GM et ducatur MC parallela AB.

Praeterea si AQ major quoque fuerit quam AG, ita tamen ut quadratum AQ non majus sit duplo quadrato ex AG. Caeteris ad eundem modum compositis haec tantum erit differentia quod arcum KP qui ex semicircumferentia reliquus est tripartito secare oportet quarum una sit PH, et subtensae GH aequalem ponere GM. Manifestum est autem, quod si AQ ipsi AG aequalis

1) Le commencement de cette minute est le même que celui de la lettre N^o. 165: c'est pourquoi on l'a supprimé ici. Quant à l'‘alterum problema’ mentionné dans le troisième alinea de cette minute il est traité beaucoup plus au long dans l'Appendice, N^o. 166. Il semble donc que cette minute-ci doit être considérée comme contenant la rédaction primitive dont Chr. Huygens, en reprenant la plume, fit les lettres N^os. 165 et 166.

[p. 244]

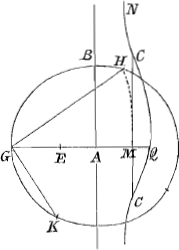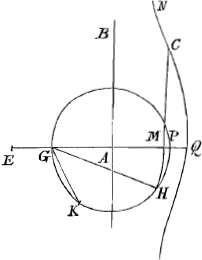fuerit, incidet E in G. Eritque tantummodo GM aequalis sumenda lateri trianguli aequilateri in circulo GHP descripti.

Item si AQ duplum potest ipsius AG²⁾, quod tum GM duplae tantum GA aequalis sumenda est. Denique ijs casibus omnibus planum fore problema quibus arcus KP vel KPG, erit ejusmodi, ut Plana Constructione trifariam secari possit. Qui sunt numero infiniti.

Qua consideratione usus fuerim ad Resolutionem opinor me tibi subindicasse, cum hic adesses. Non repetam itaque. sed alterius Problematis Constructionem tibi exscribam, de linea magnitudine data intra rhombi angulum accommodanda, quam te desiderare dicebas. Novam autem demonstrationem eamque optimam hisce demum diebus adinveni.

Si pro Rhombo quadratum fuerit datum, ad angulum exteriorem Constructio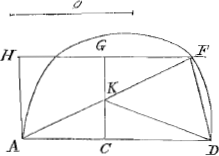



Pappi nota est. Sed ad interiorem erit haec commodissima. Quadratis ex O et CG³⁾ ponatur aequale quadratum CD et super AD semicirculus describatur et ducantur FK, fk, ut in Rhombo factum fuit. Erit autem hujus brevior demonstratio, nam junctis KD, FD, ductaque FL perpendicularis in AD quoniam similia sunt triangula ACK, FLD, et FL ∞ AC, erit et FD aequalis KA. Est autem ex constructione quadratum CD aequale quadratis O et CA. Ergo addito utrimque quadrato CK erunt quadrata KC, CD hoc est quadratum KD hoc est quadrata KF, FD simul aequalia quadratis O et KA. Demptisque aequalibus

2) Cela veut dire: si AQ² = 2 AG².

3) Voir la figure de la page suivante. La dernière de cette page-ci représente la construction de Pappus.

[p. 245]

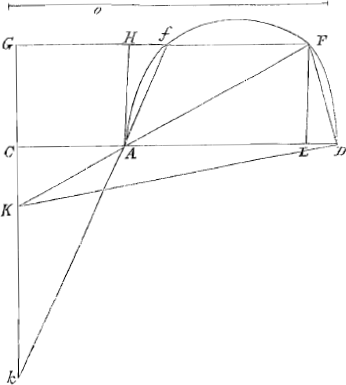utrimque hinc quadrato KA inde quadrato FD, erit quadratum KF ∞ quadrato O. ideoque linea KF lineae O datae.

Nam primum quod semicirculus super AD rectam GF secabit sic ostenditur. Etenim quia O major ponitur duplâ diametro quadrati AG, erit quadratum O majus octo quadratis ex AC, igitur quadratum CD majus novem quadratis ex AC. ac proinde CD major tripla CA. dimidia igitur AD hoc est radius semicirculi AfFD major quam AC hoc est AH, quare necessario secat lineam GF.