Oeuvres complètes. Tome I. Correspondance 1638-1656

N^o 165.
Christiaan Huygens à Fr. van Schooten.
23 octobre 1653.

La lettre et la copie se trouvent à Leiden, coll. Huygens.

Christianus Hugenius Francisco Schotenio Viro Clarissimo S.D.

Pro diligentia in comparanda Astronomia Belgica¹⁾ gratiam habeo. Ducquius²⁾ eam mihi reddidit, simulque binas constructiones ad inveniendam Conchoidis sim-

1) C'est l'ouvrage suivant, dont la première édition parut en 1653 à Harlingen chez Jan Hessels. Bientòt vint la seconde:
Nederduytsche Astronomia, Dat is: Onderwijs van den Loop des Hemels, leerende het vinden der Plaetsen en bewegingen der vasle Sterren, Son en Maen: als oock haer Eclipsen of verduystringhen. Item, den loop der Planeten, welcke door reeckeningh, en oock tuyghwerckelijck met een Planeet-wijser aangewesen wordt. Hier by gevoeght een Aen-hangh, dienende tot naeder verklaeringhe over den Loop des Hemels. Als oock eenighe voorbeelden der Son-Eclipsen, welcke rekening door verscheyden voorbeelden ghetoont wordt. Alles nut en vermakelijck, niet alleen voor de Liefhebbers deser konst, maer oock voor Schippers en Stuyrluyden. Beschreven door Dirck Rembrantsz. van Nierop, Liefhebber der Mathematische Konsten. Ende nu met den tweeden Druck, overghesien, verbetert ende vermeerdert, by den zelfden Autheur, als oock een gedruckten Planeet-Wyser. t'Amsterdam, by Gerrit van Goedesbergh, Boeck-verkooper op 't Water, in de Delftsche Bybel, over de Nieuwe Brugh. Anno 1658. in-4^o.

2) Adriaan Duyck, dit Paradijs, fils du trésorier de Hollande de même nom, et de Barbara de Heyne, naquit en 1628 à la Haye, devint étudiant à Leiden en mars 1646. Depuis il fut Lieutenant-Colonel dans l'armée des Pays-Bas.

[p. 246]

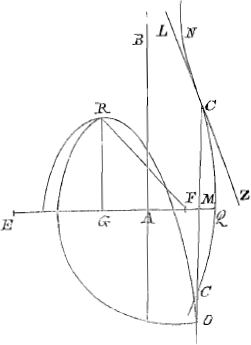plicissimae tangentem exhibuit, quas ingeniose sanè excogitasti, unam ex alia deducendo. Nam diverso quam ego calculo te usum animadvertere non potui. In Conchoide altera, quam primam vocamus, flexus punctum sequenti modo invenitur. Esto Conchoides QCN, descripta polo G et asymptoto AB; quam secet GAQ ad angulos rectos. Sit GR parallela AB, et aequalis duplae GA. Et vertice R axe RG parabola describatur RO cujus latus rectum ipsi GA aequale sit. Porro sumptâ ad duas AG, AQ tertia proportionali AE, positâque GF ipsi GE aequali, centro F, radio FR, circumferentia describatur quae parabolam secet in O. Atque hinc educta OC ipsi AB parallela ostendet in conchoide flexus punctum C. In quo si tangens ducatur LCZ ea ibidem secabit quoque conchoidem³⁾.

Haec universalis est constructio. at quando AQ non major est quam ut duplum possit ipsius AG, per trisectionem anguli expediri potest. Trisectio autem anguli ipsius ope Conchoidis quae proposita est. Adeo ut tunc quodammodo planum fiat Problema. Est autem omnino planum infinitis numero casibus quorum duos notabo. Nimirum cum AQ potentia dupla est ad AG⁴⁾, sumenda tantum est AM ipsi AG aequalis, et ducenda MC parallela AB. Rursus cum AG ipsi AQ aequalis est oportet sumere GM aequalem lateri trianguli aequilateri in circulo cujus radius AG.

Quali consideratione fuerim usus cum hoc Problema resolverem opinor me tibi subindicasse cum hic adesses. Non repetam itaque, sed alterius Problematis Constructionem tibi exscribam⁵⁾, de linea intra Rhombi angulum accommodanda quam te desiderare dicebas. Novam autem demonstrationem eamque optimam hisce demum diebus adinveni. Vale.

Domino Berckelio salutem dices meo nomine atque haec si visum fuerit imperties.

Hagae. 23 Oct. 1653.

Aen Mijn Heer De Heer Fr. van Schooten, Professor der Mathematijquen inde Universiteijt

Inde Heeresteeg.

Tot

Leijden.

3) A partir d'ici la minute de la lettre précédente diffère de cette lettre-ci; voyez la Lettre N^o. 164.

4) C'est à dire: AQ² = 2 AG².

5) Voyez les Lettres N^o. 164 et 166.