Oeuvres complètes. Tome I. Correspondance 1638-1656
(1888)–Christiaan Huygens–
[pagina 247]
| |
Pars 1.Rhombo dato, et uno latere producto aptare sub angulo exteriori lineam magnitudine datam quae ad oppositum angulum pertineat. 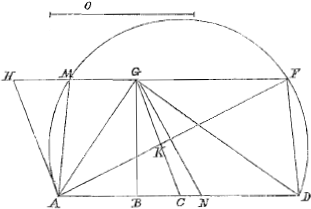 Sit datus Rhombus AHGC, cujus productum latus HG; data verò linea O. Et propositum sit ducere rectam AKF, ita ut pars intercepta KF sit datae O aequalis. Ducatur diameter AG, productoque si opus est latere AC, ponatur GD, cujus quadratum aequetur quadratis ex O et AG. Et super AD circumferentia describatur quae capiat angulum angulo rhombi AHG aequalem. Secabit ea productum latus HG. Itaque ad intersectionis punctum F ducatur AF. dico hujus partem interceptam KF datae O aequalem esse. Quod autem circumferentia descripta latus HG productum secat sic fiet manifestum. ducatur GN, ita ut sit angulus AGN angulo AHG aequalis. Itaque triangulus AGN triangulo AHG vel ACG similis est, nam et angulum ad A communem habent. Isosceles igitur triangulus AGN, ideoque si super AN circumferentia describeretur capiens angulum AHG, hoc est, AGN, ea contingeret lineam HF in puncto G. Sed AD major est quam AN; nam quadratum GD majus est quadrato GN, cum sit aequale quadratis ex GN sive GA et ex O; Idcirco GD major quam GN, ac proinde cadit GD extra triangulum AGN. Itaque manifestum est circumferentiam super AD descriptam quae capiat angulum AHG hoc est AGN secare lineam HG productam. Ducatur ex A ad alterum intersectionis punctum recta AM. junctaque FD, cadat ex G perpendicularis in AD linea GB. Quia igitur quadratum GD aequale est quadratis ex O et AG; idemque quadratum GD aequale quadratis AG, et AD minus duplo rectangulo DAB, hoc est, minus rectangulo DAN; dempto communi quadrato AG, erit quadratum O aequale quadrato AD minus rectangulo DAN; hoc est, rectangulo ADN. Est autem sicut AD ad AC ita rectangulum ADN ad contentum AC, DN. Ergo ut AD ad AC ita quo- | |
[pagina 248]
| |
que quadratum O ad contentum DN, AC, hoc est, ad excessum rectanguli DAC supra rectangulum NAC. Est autem rectangulo DAC aequale rectangulum FAK, quoniam DA ad AF ut KA ad AC, propter triangulos similes DAF, KAC: habent enim angulum ad A communem et angulus C ipsi F est aequalis. Item rectangulo NAC aequale est quadratum AG, quia propter similes triangulos est NA ad AG ut AG ad AC. Igitur excessui rectanguli DAC supra rectangulum NAC aequalis excessus rectanguli FAK supra quadratum AG. Ideoque erit ut AD ad AC ita quadratum O ad excessum rectanguli FAK supra quadratum AG. Huic verò excessui aequale est rectangulum KG, GF; quod sic ostenditur. Etenim quia quadrilaterum FDAM est in circulo sunt anguli FDA, AMF simul duobus rectis aequales, hoc est duobus simul CKA, GKA. Est autem angulus CKA aequalis FDA, propter similitudinem triangulorum DAF, KAC. Ergo et angulus GKA aequalis AMF. Trianguli igitur AGM, AGK, angulos M et K aequales habent; sed et angulos ad G et latus AG commune. Itaque dicti trianguli similes sunt et aequales. Quare GM aequalis GK, et MA aequalis AK; Et angulus KAG aequalis MAG. In triangulo igitur FAM angulus A in duo aequalia dividitur à recta AG, ideoque rectangulum FAM minus quadrato AG aequatur rectangulo MGF. Sed rectangulum FAM est rectangulum FAK; et rectangulum MGF est rectangulum KGF. Itaque rectangulum FAK minus quadrato AG, aequale rectangulo KGF, uti dictum fuit. Est igitur ut DA ad AC ita quadratum O ad rectangulum KGF. At sicut DA ad AC ita rectangulum DAC, hoc est, rectangulum FAK ad quadratum AC. Ergo quoque ut rectangulum FAK ad quadratum AC ita quadratum O ad rectangulum KGF. Ratio autem rectanguli FAK ad quadratum AC composita est ex ratione KA ad AC, hoc est KF ad FG et ex ratione FA ad AC seu AH, hoc est ratione FK ad KG. Igitur et quadrari O ad rectangulum KGF ratio composita est ex ratione KF ad FG et ratione KF ad KG. Verum ex hisce componitur quoque ratio quadrati KF ad rectangulum KGF. Igitur erit quadratum O ad rectangulum KGF ut quadratum KF ad idem rectangulum KGF: ac proinde quadratum O aequale quadrato KF, et KF linea aequalis O datae. quod erat demonstrandum. | |
Pars 2.Rhombo dato et duobus contiguis lateribus productis aptare sub angulo interiori lineam datae aequalem quae per oppositum angulum transeat. Oportet autem datam non minorem esse dupla diametro quae reliquos duos angulos jungit.
Sit datus Rhombus ACGH cujus producta sint latera GH, GC. Data vero linea O. Et oporteat ducere FAK rectam quae sit ipsi aequalis. Ducatur diameter AG eique ad rectos angulos SAR, quae quidem aequalis erit duplae diametro HC. Igitur O non minor debet esse data quam SR. Et si quidem aqualis est, factum erit quod proponebatur. Verùm ponatur O major data quam SR. Et producto latere CA ponatur GD cujus quadratum aequetur quadratis ex O et ex | |
[pagina 249]
| |
GA. Et super AD circumferentia describatur quae capiat angulum ipsi CGH aequalem.
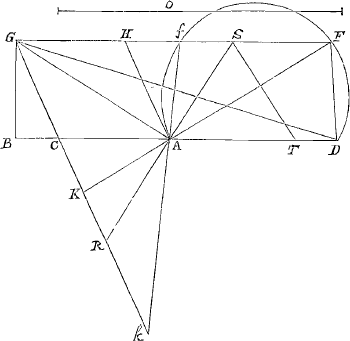 Ea secabit productum latus GH. Itaque à punctis intersectionum F, f, ducantur rectae FAK, fAk. dico harum utramque datae O aequalem esse. Quod autem circumferentia AfFD latus GH productum secat sic primum ostendetur. Sit GB ipsi AC perpendicularis et ducatur ST, ut sit angulus AST aequalis angulo CGH vel AHS. Est itaque triangulus AST triangulo AHS similis, nam et angulos ad A aequales habent: quare isosceles quoque triangulus AST. Apparet igitur lineam GS ipsi BA cum dimidia basi AT aequalem esse. quamobrem dupla GS hoc est quadrupla GH vel CA aequalis erit duplae BA cum tota AT. Et sumpta communi altitudine TA, erit rectangulum sub quadrupla AC et AT aequale duplo rectangulo BAT cum quadrato AT. additoque utrimque quadrato AB, erit rectangulum CAT quater cum quadrato AB aequale rectangulo BAT bis cum quadratis AT, AB, hoc est quadrato BT. Quia vero propter triangulos similes est TA ad AS ut AS ad AH sive AC, rectangulum CAT aequale est quadrato AS, et quater sumptum quadrato SR. Ergo quadratum SR cum quadrato AB aequale quadrato BT. Quia vero quadratum GD aequale est quadratis ex O et AG, ideo dempto communi quadrato BG, erit quadratum BD aequale quadratis ex O et AB. Ergo quadratum BD majus est quadrato BT. namque hoc aequale ostensum est quadratis SR et AB, quorum quadratum SR minus est quam quadratum O. Est ergo BD major quam BT, et proinde AD major quam AT. Si vero super AT circumferentia describatur capiens angulum aequalem CGH hoc est AST, ea continget rectam GF in puncto S, quia triangulus AST est isosceles. Igitur similis circumferentia super AD descripta, quae est Af FD, lineam GF necessario secat. Porro quod utraque harum FK, fk aequalis est datae O sic demonstrabitur. Quia quadratum GD aequale est quadratis ex O et AG, idemque quadratum GD aequale quadratis GA, AD, cum duplo rectangulo DAB; erit propterea, dempto utrimque quadrato AG, quadratuin O aequale quadrato AD cum duplo rectangulo DAB, hoc est aequale contento sub DA cum dupla AB et sub AD. Est autem hoc rectangulum ad rectangulum sub DA cum dupla AB et sub AC, sicut AD ad AC. Igitur | |
[pagina 250]
| |
ut AD ad AC, ita quoque quadratum O ad rectangulum sub DA cum dupla AB et sub AC, hoc est, ad rectangulum DAC cum duplo BAC. Est autem rectangulo DAC aequale rectangulum FAK, quoniam DA ad AF ut KA ad AC, propter triangulos similes DAF, KAC: habent enim angulos ad A aequales et angulum AFD angulo ACK. Item duplo rectangulo BAC aequale est quadratum AG: nam propter triangulos similes, ut SG, hoc est dupla AC ad GA ita est GA ad AB. Ergo rectangulo DAC cum duplo rectangulo BAC, aequantur rectangulum FAK cum quadrato GA. Quare ut DA ad AC ita erit quadratum O ad rectangulum FAK cum quadrato GA. hoc est, ad rectangulum KGF; namque in triangulo KGF angulus G in duo aequalia dividitur à linea GA. Est vero ut DA ad AC ita rectangulum DAC, hoc est rectangulum FAK ad quadratum AC. Ergo ut quadratum O ad rectangulum KGF ita rectangulum FAK ad quadratam AC. Ratio autem rectanguli FAK ad quadratum AC componitur ex ratione KA ad AC, hoc est KF ad FG, et ex ratione FA ad AC seu AH, hoc est ratione FK ad KG. Ergo quoque quadrati O ad rectangulum KGF ratio componitur ex ratione KF ad FG et ratione KF ad KG. Sed ex hisce quoque componitur ratio quadrati KF ad rectangulum KGF. Igitur quadrati O ad rectangulum KGF eadem est ratio quae quadrati KF ad idem rectangulum KGF. ac proinde quadratum O quadrato KF aequale est. Et KF lineae datae O. Quod erat demonstrandum. Pertinet autem demonstratio etiam ad lineam fk. Si pro Rhombo Quadratum fuerit datum, ad angulum quidem exteriorem Constructio Pappi nota est. Sed ad interiorem eadem erit praecedenti, hoc tantum immutando ut quadratis ex O et CG aequale ponatur quadratum CD. Demonstratio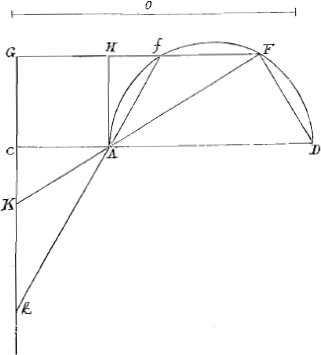 autem brevior erit. Nam primum quod circumferentia super AD, quae nunc semicirculi est, productum latus GH secabit sic ostenditur. Etenim quia O major ponitur quam dupla diameter HC, erit quadratum O majus octo quadratis AC, et proinde quadratum CD majus novem quadratis AC. quare CD major tripla CA, et dimidia AD quae est radius semicirculi AfFD major quam AC vel AH. Ideoque circumferentia lineam GF secat necessario. Ad reliquam demonstrationem jungantur FD, DK. Igitur quia similia sunt triangula ACK, AFD, erit et angulus FDA angulo AKC aequalis. Aequali autem intervallo | |
[pagina 251]
| |
distant lineae HF, AD, et HA, GK. Igitur apparet FD ipsi AK aequalem esse. Est autem ex constructione quadratum CD aequale quadratis O et AC. Ergo addito utrimque quadrato CK, erit quadratum O cum quadrato KA aequale
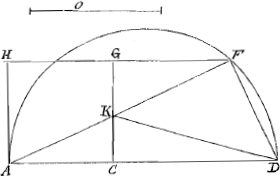 quadratis CD et CK, hoc est quadrato KD, hoc est quadratis KF, et FD. Demptisque aequalibus utrimque, hinc quadrato FD, inde quadrato AK, Erit quadratum KF aequale quadrato O, et lineae O recta KF. Quod erat demonstrandum. Eadem vero demonstratio etiam in Casu altero qui apud Pappum construitur locum habet ut videre est ex schemate adjecto. |
|

