Oeuvres complètes. Tome I. Correspondance 1638-1656

N^o 137.
A. Tacquet à Christiaan Huygens.
2 décembre 1652.

La lettre se trouve à Leiden, coll. Huygens.
Elle est la réponse au No. 133. Chr. Huygens y répondit par le No. 139.

Clarissime Domine

Humanissimis litteris tuis ac mihi longè gratissimis non respondi hactenus varijs rebus impeditus. Jam aliquantò plus nactus otij, id facio perlibenter. Pro munusculo exili ac tenui nihil sanè fuit quod gratias ageres, quando id harum rerum amantibus ac peritis suo quodam iure debebatur; Quod ad quadraturam attinet, jam inde ex illo tempore, cum primum in lucem prodijt, varias authori difficultates circa propositiones 5, 6, 7, 8, 12, 39 primae quadraturae, atque etiam circa suas quadraturas reliquas, primo coram deinde scripto proposui, quibus cum ille mihi nunquam satisfecerit, iudicaui eum quadraturam non dedisse. Nihilominus reliquum opus admiratus sum semper ac mirificè depraedicaui, authoremque ipsum inter principes Geometras semper habui. Et credo, qui opus legerit, dissentiet nemo. Porro ἐξέτασιν tuam iam pridem accuratè legi, probauique multum. Rectè authorem vrges vt exhibeat quoties ratio prima contineat secundam, ac secunda tertiam. hoc enim nisi praestet, tertiam incognitam, explicabit nunquam, ac proinde non dabit quadraturam quae a notitiâ tertiae illius rationis dependet: Quod si rationes illae sint incommensurabiles, nihil eâ viâ efficietur. Eadem difficultas etiam aliquando mihi inciderat, cum legissem censuram Marini Mercennijs¹⁾ quam habet in suis reflexionibus Mathematicis, vbi id ipsum mouet sed perobscurè. Quare non ingratum tibi futurum existimo, si quae hoc in genere mihi venerunt subinde in mentem, hic adscribam.

Jn numeris rationem primam voco quam nulla ratio numerica metitur, siue inter

1) Voyez l'ouvrage cité dans la Note 5 de la Lettre No. 85.

[p. 195]

cuius terminos nulli cadere possunt medij proportionales numeri seu integri seu fracti.

Rationes incommensurabiles, in numeris, voco eas, quas nulla ratio numerica seu rationalis vt communis mensura metitur.

Rationes absolutè incommensurabiles sunt, quas nulla ratio seu rationalis seu irrationalis metitur tanquam mensura communis.

Lemma.

Numerus primus in nulla continuè ab vnitate proportionalium serie alium locum habere potest, quam vnitati proximum.

Habeat^a) enim alium, si fieri potest in serie 1, a, b, c, d, e, ita vt d sit primus, jtaque per 11, 9,²⁾ quilibet praecedentium a, b, c, metietur primum numerum d, quod est absurdum contra hypothesim.

a) In margine: 1, a, b, c, d, e [Tacquet].

2) C'est la proposition 11 du Livre 9 des Eléments d'Euclide. Tacquet cite souvent l'auteur de la même manière.

Theorema.

In numeris ratio prima est, cuius terminorum inter se primorum alteruter saltem est numerus primus.

Nam inter duos numeros inter se primos x, z, quorum saltem vnus, puta x, primus sit; nec fracti nec integri vlli medij proportionales inueniuntur: quod sic ostendo.

Cadant^b) enim, si fieri potest, inter x et z primum numeri integri proportionales medij a, b, c. Quia igitur x et z inter se primi sunt, quot inter ipsos cadunt medij proportionales, totidem inter ipsos quoque singulos et vnitatem cadent medij proportionales d, e, f, ac g, h, k, per 9, 8. Ergo in serie proportionalium 1, f, e, d, x, primus numerus x alium tenet locum, quàm vnitati proximum, quod repugnat lemmati.

Cadant^c) deinde inter x et z medij proportionales fracti, si fieri potest, a/b, c/d, e/f: et reuocentur omnes tam integri x, z, quam fracti^d) ad fractiones eiusdem denominationis o/p, l/p, m/p, n/p, s/p, erunt igitur etiam hae continuè proportionales. Quoniam uerò eundem omnes habent denominatorem, p, erunt numeratores o, l, m, n, s, fractionibus proportionales, adeoque ipsi quoque o, l, m, n, s, continuè proportionales erunt. Jgitur inter extremos o et s cadunt medij proportionales integri l, m, n. Jam quia per constructionem x et z sunt aequales o/p et s/p, erit x ad z ut o/p ad s/p, hoc est ut o ad s. Ergo cum inter o et s medij cadant l, m, n, etiam inter x et z cadent totidem medij per 8, 8^ui. Quod repugnat primae parti. Liquet igitur propositum.

b) In margine:



[Tacquet].

c) In margine: [Tacquet].

d) In margine: [Tacquet].

Theorema 2.

Dantur rationes numericae, incommensurabiles.

Nam si per theorema praecedens exhibeantur duae rationes^e) primae x ad z, v ad y, harum neutram vlla ratio numerica metietur. Ergo neque vlla numerica ratio

e) In margine:



[Tacquet].

[p. 196]

ambas ut mensura communis metietur. Ergo per definitionem erunt incommensurabiles.

Jgitur ex jam demonstratis concludemus, rationes a te vir clarissime adductas esse numericè incommensurabiles, rationes videlicet 203 ad 53 et 11 ad 5. Nam 203, 53 sunt numeri inter se primi, et eorum vnus 203, imo et alter 53 sunt numeri absolute primi. similiter 11, 5 sunt numeri absolute primi, adeoque et primi inter se. Ambae igitur rationes illae sunt primae hoc est nullam habent rationem numericam se mensurantem, per theorema 1. Ergo per theorema 2. sunt incommensurabiles, hoc est nulla numerica ratio simul vtrasque metitur. Nunquam igitur dicet Gregorius, siquidem in numeris maneat, quoties prima ratio secundam contineat.

At si relictis numeris ad magnitudines se conuertat, aliâ quâdam viâ instituenda erit disquisitio. Inprimis nulla ratio magnitudinum etiam commensurabilium reperiri potest quae sit prima siue quam nulla ratio metiatur, cum inter quaslibet magnitudines inueniri possit media proportionalis, imo mediae quotcunque; ac proinde quaelibet ratio magnitudinum diuidi possit in rationes quotcunque aequales, adeoque harum quaelibet rationem primò positam metiatur. Quare cum nullae magnitudinum rationes dentur primae, dubitari poterit vtrum reperiri possint rationes magnitudinum inter se incommensurabiles.

Esto igitur

Theorema.

Dantur in magnitudinibus rationes inter se absolutè incommensurabiles.

Sit hyperbole CFK, eiusque asymptoti BA, AL. Jnter hyperbolam et asymptotum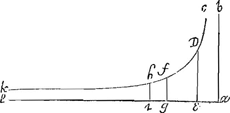



LA ponantur rectae DE, FG, HI, parallelae asymptoto alteri AB. Si plana DFGE, HFGI, sint commensurabilia, quam multiplex est planum DFGE plani HFGI, tam multiplex erit ratio DE ad FG rationis FG ad HI. Quod si plana illa incommensurabilia sint, erunt quoque rationes DE ad FG, et FG ad HI, inter se absolutè incommensurabiles. Primum demonstratur a Gregorio libro 6 propositione 125. Alterum propositione 129. Quae quidem illius speculatio omnis de spacijs asymptoticis digna planè est quam admirentur et legant Geometrae.

Jtaque si rationum illarum trium, quas propositionibus 12, et 39 proponit Gregorius, incommensurabiles sint absolutè, vel prima et secunda solae; vel secunda et tertia solae; erunt propositiones 12 et 39 falsae; sin existentibus primâ et secundâ incommensurabilibus, etiam secunda et tertia incommensurabiles sint, non poterit exponere quoties secunda ratio tertiam incognitam contineat, ac proinde per eam viam haec nunquam innotescet. Oportebit igitur Gregorium, vt tertiam rationem illam incognitam, notam reddat, demonstrare rationes à se propositas esse omnes inter se commensurabiles, rationemque ipsam quae communis mensura est, in rectis lineis exhibere, atque

[p. 197]

insuper ostendere quoties ea mensura rationes primam ac secundam ingrediatur, tunc enim innotescet quoties prima aut quomodo, secundam contineat.

Haec sunt Domine Clarissime quae mihi hac super re occurrebant. quae licet mittamus omnia, nihilo tamen magis quadratura prima subsistet, cum liquidò certòque compererim propositiones 12 et 39 esse absolutè falsas. Quadraturas 2, 3, 4 sentio non esse primâ firmiores. Caeterum Doctissima ἐξέτασις tua placet mirificè; miratusque sum cum legerem, te viri sensa hac in parte satis implexa, adeo perspicuè assecutum. Quod ad primam opusculi tui partem attinet est sanè quod tibi gratuler, quod ea isthic inueneris, quae inter illustria inuenta geometrica censeri posse existimo.

Venio ad alteram epistolae tuae partem, vbi quaeris An et quomodo elici directè possit ex falsis verum. Jllustre huiusmodi ratiocinij exemplum praebet Euclides propositione 12 libri 9. et Theodosius³⁾ libri 1 sphaericorum propositione 12. Cardanus⁴⁾ quoque libri 5. de proportionibus propositione 201 simili argumentatione est vsus. Nos quoque varia subinde eo modo demonstrauimus. Vnum profero, in quod incidi, cum theorema quoddam in refractionibus inuestigarem.

3) Theodosii Tripolitae Sphaericorum Libri III. A Christophoro Clavio Bambergensi Societatis Jesv perspicvis demonstrationibvs, ac scholijs illustrati. Item Eiusdem Christophori Clavii Sinvs. Lineae Tangentes. et Secantes. Triangvla rectilinea. atqve Sphaerica. Romae. Ex Typographia Dominici Basae. m.d.lxxxvi. in-4^o.

4) Hieronymy Cardani Mediolanensis, Civisqve Bononiensis, Philosophi, Medici et Mathematici clarissimi, Opvs Novvm de proportionibvs nvmerorvm, motvvm, pondervm, sonorvm, aliorvmque rervm mensurandarvm, non solum Geometrico more stabilitum, sed etiam uarijs experimentis & obseruationibus rerum in natura, solerti demonstratione illustratum, ad multiplices usus accommodatum, & in V libros digestum. Praeterea Artis Magnae, sive de Regvlis Algebraicis, liber vnvs, abstrvsissimvs & inexhaustus plane totius Arithmeticae thesaurus, ab authore recens multis in locis recognitus & auctus. Item de Aliza Regvla Liber, hoc est Algebraicae Logisticae suae, numeros recondita numerandi subtilitate secundum Geometricas quantitates inquirentis, necessaria Coronis, nunc demum in lucem edita. Opus Physicis & Mathematicis inprimis utile & necessarium. Basileae. in-folio.
Ce livre sort ex Officina Henric. Petrina, Anno cIƆ.IƆ.lxxiix, ainsi qu'il résulte d'un autre ouvrage de Cardanus intitulé: In Cl. Ptolemaei de astrorum jvdiciis, Libros IV, Commentarii.

Lemma.

Esto quadratum IC, cuius bina latera protrahantur in B et G, vt AB. HG, sint laterum semisses; ducaturque BG secans latera quadrati in L et K. Tum BG bisecetur in F et iunge BC.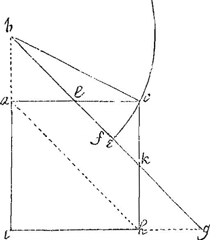

1^o Erunt latera AC, HC bisecta in L et K. 2^o Erit BK par diametro quadrati. 3^o Erit BF quadratum bis sumptum aequale quadratis BC, CH.

Duo prima patent. Tertium sic ostenditur. Quadratum BG aequatur quadratis BI, IG. Ergo eius semissis, quadratum nempe BF bis sumptum, aequatur quadrato BI. Sed quadratum BI est quadratum IA, AB et rectangulum IAB bis. Ergo quadratum BF bis, aequatur quadratis IA, AB et IAB bis. Sed IAB bis est quadratum IA. Ergo quadratum BF bis aequatur quadrato IA bis cum quadrato AB, hoc est quadratis BC, CH.

[p. 198]

Theorema.

Jisdem positis, dico rectam BG maiorem esse rectis BC, CH^f).

Si negas 1 sit non maior. Centro B per C eat circulus secans BG in F⁵⁾. Quoniam BG ponitur non maior quam BCH, estque BE par BC, patet BE maiorem esse semisse ipsius BG. Cum enim BC sit maior semisse BCH, erit quoque BC, hoc est BE, maior semisse ipsius BG quae est non maior quam BCH. Accipiatur ergo BF dimidia BG. Quoniam igitur BG bisecta est in F et aliter in E, erunt quadrata BE, EG aequalia per 9. 2. quadrato BF bis (hoc est per lemma, quadratis BC, CH) et quadrato FE etiam bis. Ergo quadrata BE, EG simul maiora sunt quadratis BC, CH simul. Quare ablatis aequalibus quadratis BC, BE, remanet quadratum EG maius quadrato CH. Ergo recta EG maior est rectâ CH. sed aequales sunt BE, BC. Ergo tota BG maior est duabus BC, CH.

Jtaque ex eo quod BG ponebatur non maior duabus BC, CH, directè conclusimus, BG maiorem esse duabus BC, CH. Neque erit difficile, vti arbitror, ratiocinationis istiusmodi, quae admirationem plerisque mouet, hic obiter causam insinuare. Proprium est propositioni falsae, vt ex eâ deduci possint contradictoria, quae proinde in ipsâ mediale seu virtualiter continentur. Jam licet plerumque contradictoria illa sint ab ipsa propositione distincta vtraque: fit tamen subinde, vt eorum alterum sit ipsa falsa propositio; alterum propositionis falsae negatio. Quod quando euenit, tum enimuero potest ex ipso falso eius negatio elici, hoc est verum; nam falsi negatio, est verum. Atque id quidem est falsi naturae omninò consentaneum, neque magis mirum est ex falso elici posse verum, quam in falso contineri contradictoria, quorum alterum sit falsum ipsum, alterum negatio eiusdem falsi.

Simili forma probationis demonstraui partem minimam, quae a triangulo per datum in ipso punctum abscinditur, Non trapezium esse, sed triangulum. Studui enim aliquando plenam dare solutionem eius problematis, quo iubetur triangulum per datum punctum secari in ratione data, quod in illo, praesertim quando punctum datur intra triangulum, non leuis insit difficultas, et neque a Steuinio⁶⁾ neque a Joanne Benedicto⁷⁾ alioue vllo, quem uidere mihi contigerit, data esset solutio adae-

f) In margine: Mutatâ inter scribendum demonstratione, duo prima sunt superflua. [Tacquet.]

5) Lisez: E.

6) Problematvm Geometricorvm in gratîam D. Maximiliani, Domini a Crvningen &c. editorum, Libri V. Auctore Simone Stevinio Brvgense. Antverpiae, apud Ioannem Bellerum ad insigne Aquilae aureae. [1583]. in-4^o.

7) Giovanni Baptista Benedetti, né à Venise le 14 août 1530 et mort à Turin le 20 janvier 1590, disciple de Tartaglia, était Mathématicien du Duc de Savoye. Tacquet parle ici de son ouvrage:
Resolvtio omnium Evclidis Problematvm aliorumque ad hoc necessario inuentorum vna tantummodo circini dato apertura, per Ioannem Baptistam de Benedictis inventa. Venetiis. m.dliii. in-4^o.

[p. 199]

quata. Cum igitur id aliâ quâdam viâ tentarem, assecutus tum quidem sum, quod proposueram: at simul contemplatio non iniucunda de maximis minimisque triangulis per datum in triangulo punctum secabilibus, atque istud, quod iam dixi, quoddam quasi lemma ad caeteras, sese obtulit. Cuius quidem demonstratione hic adscribendâ (quamuis non difficulter non hanc modò dare possem sed etiam plures) supersedeo, quod ijs, quae iam scripsi supra, satisfactum putem dubitationi tuae. Porro iam finire cupienti, quae ad tuum de hyperbola pulcherrimum theorema, tibi verè (vt scribis) ante omnes primo perspectum, secundâ paginâ praefatus es, in mentem veniunt, monentque vt adiungam adhuc aliquid, tibi forte non ingratum; repertam videlicet esse a me proportionem aliquam circuli ad hyperbolam, et eam quidem quae fortè probet determinationem in hyperbola etiam Archimedeae illi parabolicae similem posse reperiri. Scito igitur proportionem circuli ad hyperbolam terminatam esse compositam ex tribus rationibus; ex ratione circumferentiae circuli ad ⅔ diametri, et ex ratione tertiae partis quadrati circulo inscripti ad triangulum maximum hyperbolae inscriptum, et ex ratione eiusdem trianguli ad hyperbolam: cuius demonstrationem ex nostris cylindricorum et annularium libris⁸⁾, iam tibi fortasse notis, facile deduco. Jtaque ne datâ quidem hyperboles quadraturâ, dabitur in rectis lineis eius ad circulum ratio, ac proinde neque circuli quadratura. Quare cum non videatur, quadraturae circuli, hyperboles quadratura implicari, non haec ἀδύνατος perinde atque illa videri possit. Hanc meam coniecturam confirmat Bartholomaeus Souerus⁹⁾ in fine praefationis ante librum 5, proportionis curuae ad rectum promotae¹⁰⁾; vbi asserit repertam esse a se dimensionem ac quadraturam hyperbolae, sed eam se dare seorsim velle, vt nouum inuentum lectorum animos in maiorem sui admirationem conuertat. Sed (credo) quod statuerat morte praepeditus exequi non potuit. Plura non addo vt finis aliquando sit.

Tu eo animo ista accipe, quo ego scripsi, vnâ videlicet tibi obsequendi impulsus voluntate. Caeterum enixè precor, ne (vt vatis Diuini vtar verbis) ille scientiarum Dominus, quando eâ te ad omnem subtilitatem indole esse voluit, quidquam te earum

8) Voyez la Note 5 de la Lettre No. 102.

9) Bartolomeo Sovero naquit en 1577 à Corberia (Fribourg, Suisse) et mourut à Venise le 23 juillet 1629. Après avoir fait ses études au Collège Helvétique de Turin, il se rendit à Rome (1621), puis fut appelé par Camillus Gloriosus à Venise (1624), auquel il succéda comme professeur de mathématiques.

10) Cvrvi ac recti proportio a Bartholomeo Sovero Fribvrgensi. in Gymnasio Patauino Matheseos Professore promota. Libris sex ad Illustris. & Excellentis. Viros Nicolavm Contarenvm, Iohannem Baptistam Nani, Dominicvm Molinvm eiusdem Gymnasii Patavini moderatores. Patavii, Ex Typographia Varisci Varisii. m.dc.xxx. in-4^o.

[p. 200]

rerum latere sinat, quibus sempiterna beatitudo nostra ac salus continetur. Vale, et si quae properanti exciderint calamo liturae, condona.

Tuus in Christo Seruus

Louanij 2 Decemb. 1652.

Andreas Tacquet e societate Jesv.